Проверка гипотезы о значимости уравнения регрессии в целом

При отсутствии линейной зависимости y от x (то есть в случае y = e) статистики и имеют c ²–распределение с числом степеней свободы N -2 и 1 соответственно. Действительно, в этом случае

,

где e_i – нормально распределенные случайные величины с нулевым математическим ожиданием и средним квадратичным уклонением 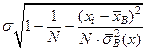. При этом эти случайные величины e_i подчиняются двум линейно независимым соотношением, следовательно, при достаточно больших N, статистика распределена по закону c ² с N -2 степенями свободы.

Аналогично, для статистики D_R имеем:

, где , .

Подставляя в сумму для D_R, получим

.

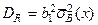При этом b ₁ нормально распределена с математическим ожиданием a ₁ = 0 и средним квадратичным уклонением 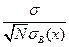.Следовательно, статистика распределена по закону c ² с 1 степенью свободы.

Теперь мы можем найти закон распределения коэффициента детерминации и сформулировать критерий незначимости уравнения регрессии с заданным уровнем значимости. Для этого нам потребуется знание еще одного распределения, а именно, распределение Фишера–Снедекора, или F –распределения.

Рассмотрим случайную величину

,

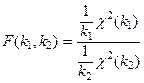где – независимые случайные величины с числом степеней свободы k_i. Случайная величина 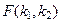называется F–распределением с числом степеней свободы 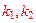. Функция плотности F –распределения имеет вид

.

Можно показать, что статистики и являются независимыми, поэтому случайная величина

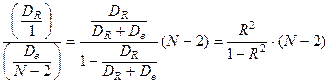
имеет F –распределение с числом степеней свободы 1, N -2. Это дает следующий критерий проверки гипотезы о незначимости уравнения регрессии.

Зададимся уровнем значимости a и найдем критическую точку 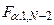F –распределения с числом степеней свободы 1, N -2 и данным уровнем значимости. Для этого следует решить уравнение

.

Для вычисления 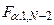можно использовать следующие команды программ как EXCEL, MATHCAD и MAPLE.

> with(stats):statevalf[icdf,fratio[k1,k2]](1-a); (Maple)

qF(1-a,k1,k2) (MathCad)

=FРАСПОБР(a;k1;k2) (Excel)

В частности, .

Уравнение регрессии признается незначимым на уровне значимости a, если .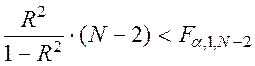

Иначе, гипотеза о незначимости уравнения регрессии отвергается.

Дата добавления: 2014-12-16