Временные параметры сетевых графиков

Понятие пути сетевого графика

Одно из важнейших понятий сетевого графика – понятие пути. Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы. Среди различных путей сетевого графика наибольший интерес представляет полный путь L – любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим. Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими называются также работы и события, расположенные на этом пути. По существу, критический путь – «узкое» место проекта. Уменьшить общую продолжительность осуществления проекта можно, только изыскав способы сокращения работ, лежащих на критическом пути. Таким образом, нет никакой необходимости в часто практикуемом стремлении «поднажать» на всех работах ради сокращения общей длительности выполнения проекта. В больших проектах критическими бывают примерно 10% работ.

Для рассмотренного в примере 1 сетевого графика полными путями будут: путь 1®2®4®7®8 (продолжительностью 10+30+0+20=60 минут), путь 1®2®5®6®7®8 (продолжительностью 10+0+40+0+20=70 минут), путь 1®3®4®7®8 (продолжительностью 20+0+0+20=40 минут), путь
1®3®5®6®7®8 (продолжительностью 20+20+40+0+20=100 минут). Последний путь имеет наибольшую продолжительность и является критическим. Продолжительность критического пути составляет 100 минут. Быстрее работу выполнить нельзя, так как для достижения завершающего события критический путь надо пройти обязательно.

Время, необходимое для выполнения некритических работ, не имеет значения с точки зрения продолжительности осуществления проекта в целом. Иначе говоря, все ненапряженные пути имеют резервы времени. Эти резервы определяются вычитанием из критического пути продолжительности данного некритического пути.

В таблице 3 приведены основные временные параметры сетевых графиков.

Важнейшим показателем сетевого графика являются резервы времени [20]. Резервы времени каждого пути показывают, на сколько может быть увеличена продолжительность данного пути без ущерба для наступления завершающего события. Поскольку каждый некритический путь сетевого графика имеет свой полный резерв времени, то и каждое событие этого пути имеет свой резерв времени.

Таблица 3

Элемент сети	Наименование параметра	Условное обозначение параметра
Событие i	Ранний срок свершения события Поздний срок свершения события Резерв времени события	tp(i) t(i) R(i)
Работа (i, j)	Продолжительность работы Ранний срок начала работы Ранний срок окончания работы Поздний срок начала работы Поздний срок окончания работы Полный резерв времени работы	t(i,j) tрн(i,j) tpo(i,j) tпн(i,j) tпо(i,j) Rп(i,j)
Путь L	Продолжительность пути Продолжительность критического пути Резерв времени пути	t(L) tkp R(L)

Для определения резервов времени по событиям сети рассчитывают наиболее ранние (t^p)и наиболее поздние (t^п) сроки свершения событий. Любое событие не может наступить прежде, чем свершатся все предшествующие ему события и не будут выполнены все предшествующие работы. Поэтому ранний (или ожидаемый) срок t_p(i) свершения i-го события определяется продолжительностью максимального пути, предшествующего этому событию:

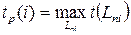, (1)

где L_ni – любой путь, предшествующий i-му событию, то есть путь от исходного до i-го события сети.

Если событие j имеет несколько предшествующих путей, а следовательно, несколько предшествующих событий i, то ранний срок свершения события j удобно находить по формуле:

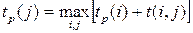. (2)

Задержка свершения события i по отношению к своему раннему сроку не отразится на сроке свершения завершающего события (а значит, и на сроке выполнения комплекса работ) до тех пор, пока сумма срока свершения этого события и продолжительности (длины) максимального из следующих за ним путей не превысит длины критического пути. Поэтому поздний (или предельный) срок t_п(i) свершения i-го события равен:

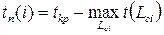, (3)

где L_ci – любой путь, следующий за i-м событием, т.е. путь от i-го до завершающего события сети.

Если событие i имеет несколько последующих путей, а следовательно, несколько последующих событий j, то поздний срок свершения события i удобно находить по формуле:

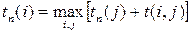. (4)

Резерв времени R(i) i-го события определяется как разность между поздним и ранним сроками его свершения:

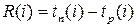. (5)

Резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ.

Критические события резервов времени не имеют, так как любая задержка в свершении события, лежащего на критическом пути, вызовет такую же задержку в свершении завершающего события. Таким образом, определив ранний срок наступления завершающего события сети, мы тем самым определяем длину критического пути.

В качестве примера определим временные параметры событий и критический путь для сетевого графика, изображенного на рис. 1. Найденные параметры сведем в таблицу 4.

При определении ранних сроков свершения событий t_p(i) двигаемся по сетевому графику слева направо и используем формулы (1), (2).

Для i=1 (начального события) t_p(1)=0. Для i=2 t_p(2)= t_p(1)+ +t(1,2)=0+10=10 (мин), так как для события 2 существует только один предшествующий путь 1®2. Для i=3 t_p(3)= t_p(1)+ t(1,3)=0+20=20, так как для события 3 существует один предшествующий путь 1®3. Для i=4 t_p(4)=max{ t_p(2)+ t(2,4); t_p(3)+t(3,4)}={10+30;20+0}=40, так как для события 4 существуют два предшествующих пути 1®2®4 и 1®3®4 и два предшествующих события – 2 и 3. Аналогично определяем сроки раннего начала для остальных событий сети:

t_p(5)= max{ t_p(2)+t(2,5); t_p(3)+t(3,5)}=max{10+0; 20+20}=max{10;40}=40;

t_p(6)= t_p(5)+t(5,6)=40+40=80;

t_p(7)= max{ t_p(4)+t(4,7); t_p(6)+t(6,7)}=max{40+0; 80+0}=max{40;80}=80;

t_p(8)= t_p(7)+t(7,8)=80+20=100.

Длина критического пути равна раннему сроку свершения завершающего события 8:

t_kp=t_p(8)=100 (мин).

Таблица 4

Номер	Сроки свершения события, мин	Резерв времени,
события	ранний tp(i)	поздний tп(i)	мин R(i)

При определении поздних сроков свершения событий t_п(i) двигаемся по сети в обратном направлении, то есть справа налево и используем формулы (3), (4).

Для i=8 (завершающего события) поздний срок свершения события должен равняться его раннему сроку (иначе изменится длина критического пути): t_п(8)= t_р(8)=100 (мин).

Для i=7 t_п(7)= t_п(8)- t(7,8)=100-20=80, так как для события 7 существует только один последующий путь 7®8.

Для i=6 t_п(6)= t_п(7)- t(6,7)=80-0=80, так как для события 6 существует только один последующий путь 6®7®8.

Для i=5 t_п(5)= t_п(6)- t(5,6)=80-40=40, так как для события 5 существует только один последующий путь 5®6®7®8.

Для i=4 t_п(4)= t_п(7)- t(4,7)=80-0=80, так как для события 4 существует только один последующий путь 4®7®8.

Для i=3 t_п(3)=min{t_п(4)- t(3,4); t_п(5)- t(3,5)}=min{80-0; 40-20}=min{80; 20}=20, так как для события 3 существует два последующих пути 3®4®7®8 и 3®5®6®7®8.

Для i=2 t_п(2)=min{ t_п(4)- t(2,4); t_п(5)- t(2,5)}=min{80-30; 40-0}=min{50; 40}=40, так как для события 2 существует два последующих пути 2®4®7®8 и 2®5®6®7®8.

Для i=1 t_п(1)=min{ t_п(2)- t(1,2); t_п(3)- t(1,3)}=min{40-10; 20-20}=min{30; 0}=0.

По формуле (5) определяем резервы времени i-го события:

R(1)=0; R(2)=30; R(3)=0 и т.д.

Резерв времени события 2 - R(2)=30 означает, что время свершения события 2 может быть задержано на 30 минут без увеличения общего срока выполнения проекта. Анализируя таблицу 4, видим, что не имеют резервов времени события 1,3,5,6,7,8. Эти события и образуют критический путь.

Теперь перейдем к параметрам работ.

Отдельная работа может начаться (и окончиться) в ранние, поздние и другие промежуточные сроки. При оптимизации графика возможно любое размещение работы в заданном интервале.

Очевидно, что ранний срок t_рн(i,j) начала работы (i,j) совпадает с ранним сроком наступления начального (предшествующего) события i, то есть

t_рн(i,j)= t_р(i). (6)

Тогда ранний срок t_ро(i,j) окончания работы (i,j) определяется по формуле

t_ро(i,j)= t_р(i)+ t(i,j). (7)

Ни одна работа не может окончиться позже допустимого позднего срока своего конечного события j. Поэтому поздний срок t_по(i,j) окончания работы (i,j) определяется соотношением:

t_по(i,j)= t_п(j), (8)

а поздний срок t_пн(i,j) начала этой работы – соотношением

t_пн(i,j)= t_п(j)- t(i,j). (9)

Прежде чем рассматривать резервы времени работ, обратимся к резерву времени пути. Такие резервы имеют все некритические пути. Резерв времени пути определяется как разность между длиной критического и рассматриваемого пути:

R(L)= t_kp-t(L). (10)

Он показывает, на сколько в сумме могут быть увеличены продолжительности всех работ, принадлежащих этому пути. Любая из работ пути L на его участке, не совпадающем с критическим путем (замкнутым между двумя событиями критического пути), обладает резервом времени.

Полный резерв времени R_п(i,j) работы (i,j) показывает, на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится. Полный резерв R_п(i,j) определяется по формуле:

R_п(i,j)= t_п(j)- t_р(i)- t(i,j). (11)

Полный резерв времени работы равен резерву максимального из путей, проходящего через данную работу. Этим резервом можно располагать при выполнении данной работы, если ее начальное событие свершится в самый ранний срок, и можно допустить свершение ее конечного события в самый поздний срок. Важным свойством полного резерва времени работы является то, что он принадлежит не только этой работе, но и всем полным путям, проходящим через нее.

Работы, лежащие на критическом пути, так же, как и критические события, резервов времени не имеют.

Вычислим в качестве примера временные параметры работ для сетевого графика, изображенного на рис. 1. Результаты вычислений сведем в таблицу 5.

Таблица 5

Работа	Продолжитель-	Сроки начала и окончания работы	Резервы времени
(i,j)	ность работы t(i,j)	tрн(i,j)	tро(i,j)	tпн(i,j)	tпо(i,j)	работы Rп(i,j)
(1,2)
(1,3)
(2,4)
(2,5)
(3,4)
(3,5)
(4,7)
(5,6)
(6,7)
(7,8)

Вычисление временных параметров работы (i,j) покажем на примере работы (2,4).

Ранний срок начала работы (по формуле (6)): t_рн(2,4)= t_р(2)=10. Ранний срок окончания работы (по формуле (7)): t_ро(2,4)= t_р(2)+ t(2,4)=10+30=40. Поздний срок начала работы (по формуле (9)): t_пн(2,4)= t_п(4)- t(2,4)=80-30=50. Поздний срок окончания работы (по формуле (8)): t_по(2,4)= t_п(4)=80.

Таким образом, работа (2,4) должна начаться в интервале [10, 50] и окончиться в интервале [40, 80] от начала выполнения проекта.

Полный резерв времени работы (2,4) (по формуле (11)): R_п(2,4)= t_п(4)- t_р(2)- t(2,4)=80-10-30=40, то есть срок выполнения данной работы можно увеличить на 40 минут, при этом срок выполнения комплекса работ не изменится.

Покажем на примере работы (2,4), что полный резерв времени работы равен резерву максимального из путей, проходящих через эту работу.

Через работу (2,4) проходит один полный путь: 1®2®4®7®8 продолжительностью 60 минут. По формуле (10) его резерв R(L)= t_kp-t(L)=100-60=40. Как видим, полный резерв времени работы (2,4) равен резерву времени максимального (и единственного) полного пути, проходящего через эту работу. Если увеличить продолжительность работы (2,4) на 40 минут, то полностью будет исчерпан резерв времени этого пути, то есть этот путь станет также критическим.

Следует отметить, что кроме полного резерва времени работы выделяют еще три разновидности резервов. Частный резерв времени первого вида R₁ – часть полного резерва времени, на которое можно увеличить продолжительность работы, не изменив при этом позднего срока ее начального события. R₁ находится по формуле:

R(i,j)= R_п(i,j)- R(i). (12)

Частный резерв времени второго вида, или свободный резерв времени R_c работы (i,j) представляет собой часть полного резерва времени, на которое можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события. R_c находится по формуле:

R_с(i,j)= R_п(i,j)- R(j). (13)

Независимый резерв времени R_н работы (i,j) – часть полного резерва, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие начинаются в ранние сроки. R_н находится по формуле:

R_н(i,j)= R_п(i,j)- R(i)- R(j). (14)

Более подробно узнать о применении вышеперечисленных данных можно в [8], [20].

Дата добавления: 2014-12-16