Моменты функции распределения

Функция распределения (ФР) является универсальным способом описания случайной погрешности. Однако чтобы получить ФР необходимы трудоемкие исследования и расчеты. Поэтому в метрологической практике часто используются характеристики распределения вероятности, называемые моментами.

Начальный момент К-го порядка результатов наблюдений определяется следующим выражением:

a_к[Х]=

Первый начальный момент - математическое ожидание: a₁[Х]=M[Х]=m_x.

Центральный момент К-го порядка результатов наблюдений определяется по формуле:

m_k[Х]=

В теории измерений важное значение имеет 2-ой центральный момент, называемый дисперсией результатов наблюдений, или дисперсией случайной погрешности:

D[X]=D[ ]=M[(X-m_x)²]=M[ ²]=

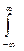= (X-m_x)²p_х(x)dx=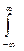 ²p_D()d .

Дисперсия случайной погрешности является характеристикой рассеяния результатов наблюдений относительно математического ожидания.

Дисперсия имеет размерность квадрата измеряемой физической величины, поэтому значительно чаще в метрологической практике пользуются средним квадратическим отклонением (СКО) результатов наблюдений, являющимся квадратным корнем из дисперсии:

s=

s₁<s₂

Рис. 4.6

Плотность вероятности результатов наблюдений при различных значениях СКО погрешности имеет следующий вид:

Чем больше s, тем более пологой и «расплывчатой» становится функция распределения (рис. 4.6). Характеристикой асимметрии функции распределения является третий центральный момент - m₃ [X]. Если ФР симметричная, то все нечетные центральные моменты равны «0» - m₁=m₃=0. Для удобства в метрологической практике вводят безразмерную характеристику асимметрии: r_k - коэффициент асимметрии.

r_k=m₃[ ]/s_x³.

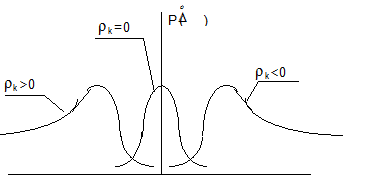
Если r_k=0 - ФР - симметричная, если r_k<0, то ее максимум находится в положительной области, если r_k>0- в отрицательной (см. рис. 4.7).

Рис 4.7
Для определения плосковершинности или островершинности плотности распределения вероятности случайной погрешности служит 4-й центральный момент m₄[x]. Свойство плосковершинности описывают с помощью эксцесса - безразмерной характеристики, которая определяется следующим образом: Е_х=(m₄[ ]/s⁴())-3.

Число 3 вычитается из дроби потому, что наиболее распространенной в практике измерений функцией распределения плотности вероятности является распределение по нормальному закону или функция Гаусса.

Для нормального закона 4-й центральный момент m₄[ 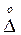]=3s⁴(). Т.е. для нормального закона распределения Е_х=0. Для более плосковершинного закона распределения Е_х<0, для более островершинного - Е_х>0 (рис. 4.8).

Моменты распределения используются для идентификации закона распределения результатов наблюдения или их случайной погрешности. В теории и практике наиболее часто встречаются и используются нормальное и равномерное распределение.

Рис 4.8

Контрольные вопросы

1 Что понимать под «моментами дифференциальной функции распределения?

2 Что такое «первый начальный момент»?

3 Что такое «дисперсия»?

4 Как определяется «плоско или остро вершинность» функции распределения?

5 Как понимается «асимметрия» дифференциальной функции распределения?

1.6 Точечная и интервальная оценки истинного значения измеряемой величины

Все бесконечное число значений физической величины называется генеральной совокупностью. На практике же всегда имеют дело с ограниченным числом наблюдений или измерений, т.е. имеют дело с выборкой из генеральной совокупности. Таким образом, оценку точности измерений проводят по ограниченному, хотя иногда и довольно большому, числу наблюдений. В результате получают одно число. Это называется точечной оценкой. Задача получения точечных оценок результатов измерений и СКО случайных погрешностей является частным случаем статистической задачи нахождения оценки параметров функции распределения случайной величины на основании выборок - т.е. ряда значений, принимаемых этой случайной величиной в ограниченном числе n независимых опытов. Независимо от закона распределения случайной величины, оцениваемыми параметрами является математическое ожидание и СКО функции распределения. Сами же формулы для оценок имеют различный вид в зависимости от закона распределения плотности вероятности. Для нормального закона в формулы для дифференциальной функции распределения математического ожидания (m_x) и СКО (s _х) входят в явном виде, а для равномерного распределения определяются из соотношений:

b=m_x+s_x m_x= ,

a=m_x-s_x s_x= .

Если есть параметр А, то его оценка называется точечной, если она выражается одним числом.

Любая точечная оценка, вычисленная на основании опытных данных, будучи их функцией, сама является случайной величиной с распределением, зависящим от трех факторов:

· закона распределения исходной случайной величины;

· самого оцениваемого параметра;

· числа опытов n.

К оценкам предъявляется три требования:

1 Состоятельность. Оценка считается состоятельной, если с увеличением числа опытов n она приближается (т.е. сходится по вероятности) к значениям оцениваемого параметра, т.е. lim_n®¥P{ =А}=1.

2 Несмещенность. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру: М[ ]=А.

3 Эффективность. Оценка называется эффективной, если ее дисперсия меньше дисперсии другой оценки данного параметра.

Что значит разные оценки одного и того же параметра?

Предположим, что имеется упорядоченный или вариационный ряд результатов наблюдений случайной величины Х:

.

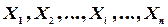Вариационный ряд - это такой ряд, в котором

Можно провести оценки различными методами: по медиане, по размаху, по среднему арифметическому и др.

Что в данном случае понимается под термином «медиана»?

Медиана Ме[Х] - это центральное среди результатов наблюдений значение случайной величины в упорядоченном ряду результатов наблюдений. В случае, когда имеется четное число наблюдений

Ме[Х]=0.5(X_(n/2)+1+X_n/2).

В случае если n нечетное число: Ме[Х]=X_(n+1)/2.

Например: при n=3, Ме[Х]=X₂, при n=4, Ме[Х]=0.5(X₂+X₃).

Оценка по размаху:

= .

Оценка по среднему арифметическому:

=

На практике не всегда удается получить оценки параметров функций распределения случайной величины, удовлетворяющие всем трем требованиям: состоятельности, несмещенности и эффективности.

Способы получения оценки зависят от закона распределения случайной величины. Для случайных величин, распределенных по различным законам, оценки параметров функций распределения проводят по различным формулам.

Для нормального закона распределения случайных величин или случайных погрешностей оценки максимального правдоподобия следующие:

, .

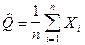- точечная оценка максимального правдоподобия.

Однако оценка дисперсии, полученная таким образом, не является несмещенной. Для получения несмещенной оценки дисперсии случайной погрешности пользуются следующей формулой:

D= , где .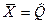

Тогда оценка СКО случайной погрешности, полученная методом максимального правдоподобия, определяется следующим образом:

,

где - несмещенная оценка генеральной средней, Х_i - оценка математического ожидания результатов наблюдений или результат наблюдений.

Для равномерного закона распределения погрешностей

; ,

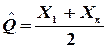Т.е. если 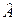- оценка максимального правдоподобия параметра А, то при достаточно большом числе наблюдений (n>25) эта оценка может считаться нормально распределенной при любом распределении результатов наблюдений, причем: при n® ¥ P{ 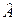= A} = 1, т.е. эта оценка состоятельная.

Интервальные оценки параметров функций распределения погрешностей или результатов наблюдений получают путем определения интервалов, в границах которых с определенной вероятностью находятся истинные значения оцениваемых параметров. Такой интервал называется доверительным, а соответствующая вероятность - доверительной вероятностью.

Доверительный интервал - интервал значений случайной погрешности, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результатов измерений. Граница доверительного интервала называют доверительными границами - верхней и нижней.

Если результаты наблюдений или погрешность результата наблюдений распределены по нормальному закону с известным СКО (s_х=s 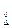), то доверительная вероятность нахождения истинного значения измеряемой величины Q в доверительном интервале [X-t_ps_x, X+ t_p s_x] определяется выражением:

Р{(X-t_ps_x)<Q£(X+t_ps_x)}=Ф(t_p)-Ф(-t_p),

где Ф(t_p) - нормированная интегральная функция нормального распределения, но поскольку Ф(z)=1-Ф(-z), т.е. Ф(-z)=1-Ф(z), то

Р={X-t_ps_x<Q£X+t_ps_x}=2Ф(t_p)-1.

Половина доверительного интервала t_ps_x называется доверительной границей случайного отклонения результатов наблюдений, соответствующего доверительной вероятности Р. Доверительный интервал, полученный по результатам многократных наблюдений, в 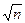раз меньше интервала, вычисленного по результатам однократного наблюдения измеряемой величины. На этом принципе основан метод снижения случайных погрешностей измерений, т.е. повышения точности результатов измерений. В принципе, увеличение n (числа наблюдений) можно получить сколь угодно малое значение случайной погрешности измерений. Однако на практике, как правило, это весьма сложно (иногда просто невозможно) сделать из-за значительного увеличения времени на проведение измерений. Особо сложно это сделать в быстро изменяющихся процессах. Поэтому необходимо выбирать минимально необходимое число наблюдений для обеспечения такой случайной погрешности, которая была бы не больше допустимой, т.е. < _доп.

Это число n для нормального закона можно определить из их соотношения:

.

Таким образом, при интервальной оценке результат не может быть выражен одним числом. В процессе измерений получают лишь среднее значение измеряемой величины и границы доверительного интервала, внутри которого находится эта измеряемая величина с принятой доверительной вероятностью. Можно сказать, что получают какую-то полосу, внутри которой находятся возможные значения измеряемой величины. Эту полосу называют «дорожкой погрешности» возможных значений Q физической величины с принятой доверительной вероятностью.

Контрольные вопросы

1 Что понимать под точечной оценкой результата измерения?

2 Что такое «интервальная оценка» результата измерения?

3 Каким условиям должна удовлетворять оценка результата измерения физической величины?

4 Как определяются границы доверительного интервала?

5 Как определяется минимально необходимое число многократных измерений?

Дата добавления: 2014-12-16