КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. Треугольники и подобны
|
|
|
|
Решение.
Треугольники 
и 
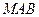подобны
Ответ: 24.
Задача 6.
Две окружности радиуса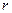 
касаются друг друга. Кроме того, каждая из них касается изнутри третьей окружности радиуса 
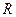в точках 
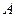и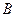 
соответственно.
Найдите радиус 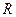, если 
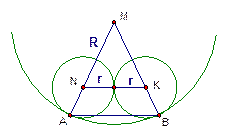Решение.
Треугольники и 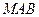подобны
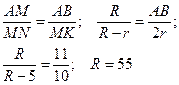
Ответ: 55
Задача 7.
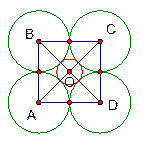Дана окружность радиуса 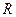. Четыре окружности равных радиусов касаются данной внешним образом, и каждая из этих четырех окружностей касается двух других. Найдите радиусы этих четырех окружностей.
Радиус маленькой окружности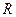
Радиусы окружностей при внешнем касании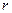
Центры окружностей расположены в вершинах квадрата
Сторона квадрата 
Диагональ квадрата 
Определим радиусы окружностей по теореме Пифагора
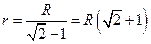
Ответ: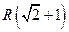 
Задача 8.
Три окружности разных радиусов попарно касаются друг друга внешним образом.
Отрезки, соединяющие их центры, образуют прямоугольный треугольник.
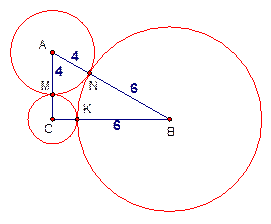Найдите радиус меньшей окружности, если радиусы большей и средней окружности равны 6 и 4.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 617; Нарушение авторских прав?; Мы поможем в написании вашей работы!