Приведення сили до даного центру

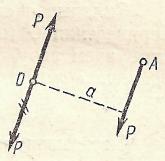
Нехай дана сила Р, що прикладена в якій-небудь точці А (рис. 3). Візьмемо довільну точку О та додамо до неї дві сили, рівні Р, їй паралельні й спрямовані в протилежні сторони.

Подібне перетворення можна розглядати як результат заміни даної сили Р іншою, паралельною їй силою Р, прикладеною в довільній точці О (на рис. 3 ця сила відзначена двома рисками), і парою (Р, Р) із плечем а, момент якої: М = + Ра.

Рис. 3.

Знак плюс у цій формулі відповідає прийнятому правилу знаків для моменту пари сил.

Заміну даної сили Р, прикладеної в точці А, силою Р, прикладеною в крапці О, і парою (Р, Р) будемо називати приведенням даної сили Р к точці О. Крапка О називається центром приведення, а пара (Р, Р) - приєднаною парою.

Не важко помітити, що момент приєднаної пари дорівнює моменту даної сили Р відносно центра приведення О.

Питання для самоперевірки

1. Що називають моментом сили відносно точки?

2. Що зветься плечем сили?

3. Як визначити знак моменту сили відносно точки?

4. В якому випадку момент сили відносно точки дорівнює нулю?

5. Чи зміниться момент сили відносно точки, якщо цю силу перенести по лінії її дії?

6. Яка пара зветься доданою?

7. Що таке центр приведення?

Питання для самостійного вивчення:

1. Визначити проекції просторових збіжних сил на вісі

2. Знайти моменти сил відносно осей для довільної просторової системи сил

3. Виконання індивідуальних завдань

Література:

Бычков В.Д. и Миров М.О. Теоретическая механика. с. 59-62.

ЛЕКЦІЯ № 8

Тема 1.3. Плоска довільна система сил.

План лекції

1. Приведення довільної системи сил до даного центру.

2. Головний вектор і головний момент.

3. Рівновага плоскої довільної системи сил.

4. Аналітична умова рівноваги.

1. Приведення довільної системи сил до даного центру

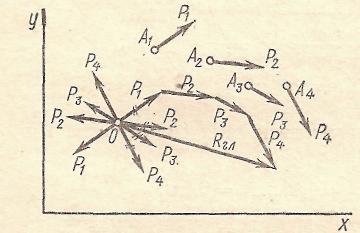
Дано систему сил (наприклад, чотири сили Р₁, Р₂, Р₃, Р₄), розташованих як завгодно на площині (рис. 1). Потрібно скласти ці сили.

Візьмемо довільну точку О і приведемо всі дані сили до цієї точки, скористуючись способом приведення сили до точки.

Рис. 1.

В результаті приведення отримаємо сили Р₁, Р₂, Р₃ і Р₄, що прикладені у точці О (позначені на рисунку двома рисками), і приєднані пари (Р₁, Р₁), (Р₂, Р₂) (Р₃, Р₃) і (Р₄, Р₄), моменти яких дорівнюють моментам даних сил відносно точки О. Тобто, позначаючи моменти пар відповідно М₁, М₂, М₃ і М₄, а моменти сил М_О(Р₁), М_О(Р2), М_О(Р₃) і М_О(Р₄), отримаємо:

М₁ = М_О(Р₁), М₂ = М_О(Р₂), М₃ = М_О(Р₃), М₄ = М_О(Р₄) (1)

Складаючи сили Р₁, Р₂, Р₃ і Р₄, прикладені в центрі приведення 0 (відзначені на рисунку двома рисками): одержуємо результуючу силу R_гл, що дорівнює їх геометричній сумі й прикладену в тій же точці О:

R_гл= Р₁ + Р₂ + Р₃ + Р₄.

Складаючи пари (Р₁, Р₁), (Р₂, Р₂) (Р₃, Р₃) і (Р₄, Р₄) - одержимо результуючу пару, момент якої М_гл дорівнює алгебраїчній сумі моментів пар, що його складають. Отже:

М_гл=М₁ + М₂ + М₃ +М₄. (2)

Маючи на увазі рівності (1), вираження (2) можна надати так:

М_гл = М₀(Р₁) + М₀(Р₂) + М₀(Р₃) + М₀(Р₄), або

2. Головний вектор і головний момент

Геометрична сума даних сил R_гл називається головним вектором, алгебраїчна сума моментів цих сил відносно центра приведення М_гл – головним моментом.

Система сил, розташованих як завгодно на площині, завжди може бути приведена до сили, що дорівнює їх головному вектору та доданій в будь-якій точці О, та до пари, момент якої дорівнює головному моменту даних сил відносно тієї ж точки.

3. Рівновага плоскої довільної системи сил

Плоска довільна система сил знаходиться в стані рівноваги тільки коли:

;

Випадки приведення ПСС:

1. , 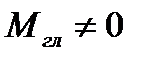- система пар сил, приводиться до пари сил (викликає обертаючу дію);

2. , 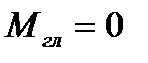- плоска система збіжних сил, приводиться до рівнодіючої (викликає поступовий рух);

3. , 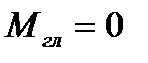- врівноважена плоска система сил.

4. Аналітична умова рівноваги

Рівняння: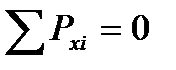

виражають аналітичні умови рівноваги плоскої довільної системи сил.

Таким чином, для того, аби тверде тіло знаходилось в стані рівноваги, необхідно та достатньо, щоб:

1) сума проекцій всіх сил на вісь х дорівнювала нулю;

2) сума проекцій всіх сил на вісь у дорівнювала нулю;

3) сума моментів всіх сил відносно будь-якої точки площини дорівнювала нулю.

Питання для самоперевірки

1. Напишіть та сформулюйте рівняння рівноваги плоскої довільної системи сил.

2. Які відомі випадки приведення плоскої системи сил?

Питання для самостійного вивчення:

1. Виконання індивідуальних завдань.

Література:

Бычков В.Д. и Миров М.О. Теоретическая механика. с. 62-68.

ЛЕКЦІЯ № 9

Тема 1.3. Плоска довільна система сил.

План лекції

1. Класифікація балок. Види опор балок та їх реакції.

2. Класифікація навантажень.

1. Класифікація балок. Види опор балок та їх реакції

Типи балок розрізняють залежно від виду опор.

Класифікація балок:

1. Балка консольна - (двох опорна) балка - проста балка

консольними частинами.

.

2. Балка шарнірна - проста(двох опорна) балка - по обох кінцях

шарнірні опори.

3. Балка – консоль. Один кінець жорстко затиснений, друг ий вільний.

4. Складена балка - складена з двох або простіших, консольних балок

консолей.

Залежно від обмежень, що накладаються, на переміщення тіла розрізняють наступні види опор: шарнірно-нерухома опора, шарнірно-рухома опора, жорстке кріплення.

Види опор балок:

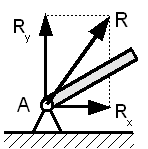
1. Шарнірно-нерухома опора - можливе обертання навколо опори,

лінійних переміщень немає, тому виникає реакція невідомої величини і напряму R, яку замінюють її проекціями на осі координат. Для плоскої системи виникають 2 невідомих реакції: Rx і Ry.

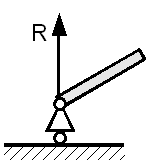
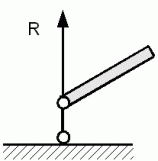
2. Шарнірно-рухома опора - зв'язок накладений тільки в одному напрямі,

т.е можливе обертання навколо опори і переміщення уздовж однієї з осей. У рухливій шарнірній опорі виникає тільки одна реакція R - сила у напрямі обмеження руху (перпендикулярно напряму рух повздовж осі)

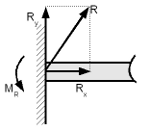
3. Жорстке кріплення - немає переміщень(жорстке закріплення тіла,

наприклад, зварювання), виникають реакція невідомої величини і напряму R і реактивний момент М_R.

Невідому реакцію зручно представити у вигляді її проекцій на осі координат будь-якого напряму, наприклад, для плоскої системи горизонтальне Rx і вертикальне Ry.

Разом: в плоскому закладенні виникають 3 невідомих реакції - 2 сили і одна пара сил.

2. Класифікація навантажень

Навантаження або сили, що діють на абсолютно тверде тіло класифікують:

1. За характером дії:

- статичні (змінюють свою величину або точку додавання з невеликою швидкістю, тобто прискоренням, що виникає можна зневажати);

- динамічні (змінюють свою величину з великою швидкістю).

2. За способом додавання:

- розподілена (що характеризується інтенсивністю q=[кН/м]);

- зосереджена (що додається в одній точці F=[кН]);

- зосереджений момент (М=[кНм]).

3. За терміном дії:

- постійні;

- тимчасові (тривалі та короткочасні).

4. Розподілені навантаження можуть бути:

- поверховими (вітрове навантаження на стіну або тиск рідини на стіну);

- об`ємними (сила тяжіння, сила інерції, магнітне тяжіння).

Питання для самоперевірки

1. Які типи балок розрізняють? І залежно від чого?

2. Назвіть види опор?

3. Класифікація навантажень.

Питання для самостійного вивчення:

1. Класифікація балок і навантажень.

Література:

Бычков В.Д. и Миров М.О. Теоретическая механика. с.72-78

ЛЕКЦІЯ № 10

Тема 1.4. Плоска довільна система сил. Методика розв’язання задач.

План лекції

1. Аналітичне визначення опорних реакцій балок. Перевірка рішень.

2. Аналітичне визначення опорних реакцій плоских рам.

Перевірка рішень.

Порядок розрахунку

Визначення опорних реакцій балки

1. Викреслити задану схему.

2. Викреслити розрахункову схему (обов'язково показати всі величини сил, відстані між прикладеними силами)

- замінюємо розподілене навантаження на рівнодіючу Q = q • a,

а - довжина ділянки на якому діє q)

- показуємо опори, позначивши їх точками А і В, подумки відкинувши опори, замінюємо їх реакціями R_A і R_B

2. Скласти рівняння рівноваги: ​​

ΣМ_А = 0

ΣМ_В = 0

3. З рівнянь визначити невідомі необхідні опорні реакції R_A і R_B

4. Виконати перевірку, використовуючи рівняння рівноваги

Σ F_iy = 0

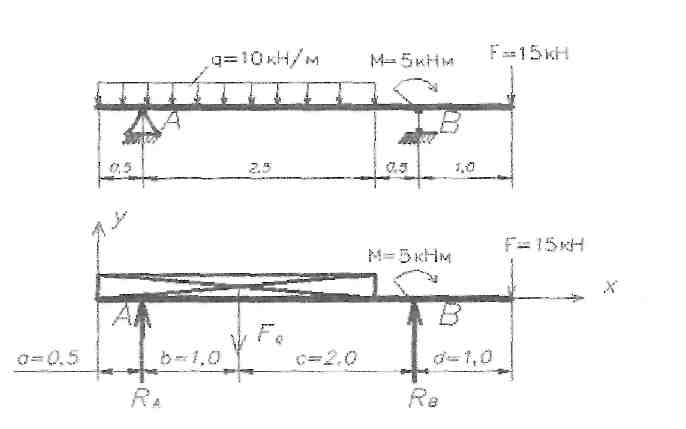
Приклад № 1. Визначити опорні реакції балки.

Рішення:

1. Замінюємо розподілене навантаження на рівнодіючу. для розподіленого навантаження рівнодіюча Fq дорівнює добутку інтенсивності q кн/м на довжину ділянки 1=0,5+2,5=Зм на якомувона діє).

2. Показуємо опори А та В.

3. Відкидаємо опори та замінюємо їх реакціями R_A та R_B.

4. Складаємо рівняння рівноваги:

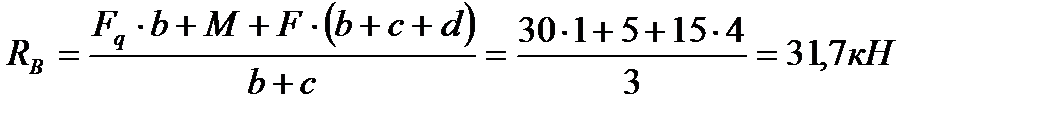
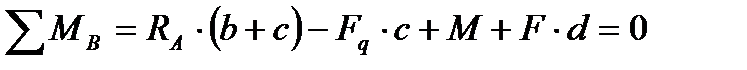
5. Виконуємо перевірку, використовуючи рівняння рівноваги.

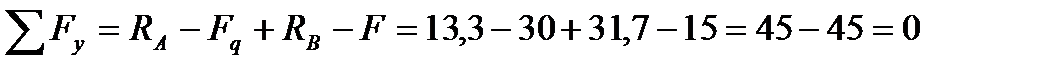
Відповідь: R_A=13,3кН; R_B=31,7кН.

Визначення опорних реакцій рами

1.Викреслити задану схему.

2. Викреслити розрахункову схему (обов'язково показати всі величини сил, відстані між прикладеними силами)

- замінюємо розподілене навантаження на рівнодіючу Q = q • a,

а - довжина ділянки на якому діє q)

- показуємо опори, позначивши їх точками А і В, подумки

відкинувши опори, замінюємо їх реакціями R_A і R_B

3. З рівняння Σ F_iх = 0, проецюючі всі сили на вісь Х визначити горизонтальну реакцію Н_А

1. Скласти рівняння рівноваги: ​​

ΣМ_А = 0

ΣМ_В = 0

2. З рівнянь визначити невідомі необхідні опорні реакції R_A і R_B

3. Виконати перевірку, використовуючи рівняння рівноваги

Σ F_iy = 0

Приклад № 1: Визначити опорні реакції рами, зображеної на рис. 8

Рішення:

1. Заміняємо розподілене навантаження рівнодіючою (для розподіленого навантаження рівнодіюча Fq дорівнює добутку інтенсивності q кн/м на довжину ділянки 1=0,5+2,5=Зм на якому вона діє).

1. Складаємо рівняння рівноваги.

1.1. для визначення горизонтальної реакції, проецюємо всі сили на вісь х:

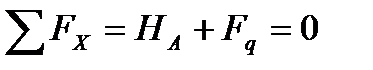
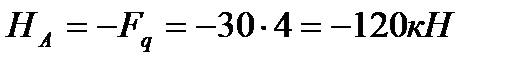
1.2. складаємо рівняння моментів відносно точок А та В для визначення вертикальних реакцій

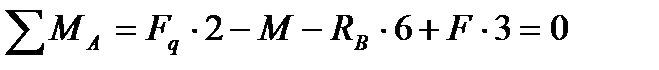
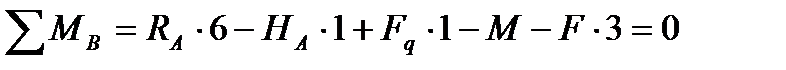
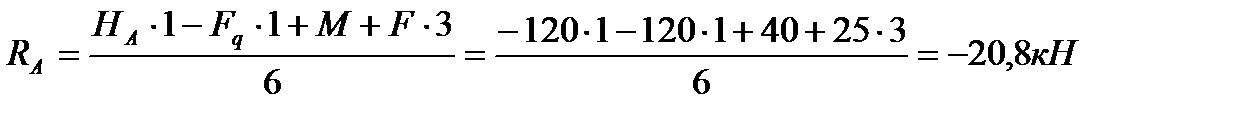
2. Виконуємо перевірку, використовуючи рівняння проекцій сил на вісь у:

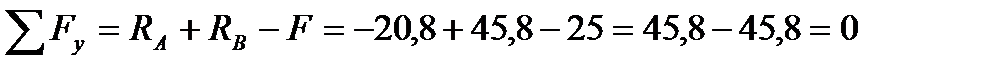
Відповідь: R_A =-20,8кН; R_B=45,8кН.

Питання для самостійного вивчення:

1. Визначення реакцій в опорах балки, рами

2. Виконання індивідуальних завдань.

Література:

Сетков В.Я. Сборник задач для расчетно-графических работ по технической механике. М.: 1988. с.14-21

ПРАКТИЧНЕ ЗАНЯТТЯ№ 11

Дивись Методичні вказівки до розрахунково-графічних робіт

з дисципліни «Теоретична механіка»

РОЗРАХУНКОВО-ГРАФІЧНА РОБОТА№ 2

Тема: Визначення опорних реакцій балки.

Мета: Закріпити теоретичні знання з теми «Плоска довільна система сил».

Навчитися розв’язувати задачі за допомогою рівнянь рівноваги.

Теоретичне обґрунтування:

Плоска довільна система сил – це система в якій сили розташовані як завгодно на площині.

Моментом сили відносно точки зветься взятий зі знаком «плюс» або «мінус» добуток величини сили на довжину перпендикуляру, що проведений з точки до лінії дії сили.

рис. 6

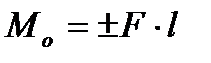
Момент буде позитивним, якщо сила намагається повернути площину креслення навколо центра (точки А) за годинниковою стрілкою, та негативним – коли навпаки. (рис. 6)

Література:

Сетков В.Я. Сборник задач для расчетно-графических работ по технической механике. М.: 1988. с.14-21, 68-71

ПРАКТИЧНЕ ЗАНЯТТЯ№ 12

Дивись Методичні вказівки до розрахунково-графічних робіт

з дисципліни «Теоретична механіка»

РОЗРАХУНКОВО-ГРАФІЧНА РОБОТА№ 3

Тема: Визначення опорних реакцій рами

Мета: Закріпити теоретичні знання з теми «Плоска довільна система сил». Навчитися розв’язувати задачі за допомогою рівнянь рівноваги.

Теоретичне обґрунтування:

Момент сили відносно точки М [кНм] взятий зі знаком плюс чи мінус твір величини сили на довжину перпендикуляра, опущеного з точки на лінію дії сили (плече): М_{0 (F)} = ± F·а

Аналітична умова рівноваги ПДСС

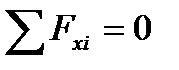
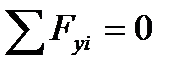
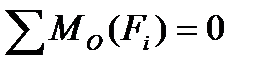
З рівняння Σ F_iх = 0, проецюючі всі сили на вісь Х визначити горизонтальну реакцію Н_А

Скласти рівняння рівноваги: ​​

ΣМ_А = 0

ΣМ_В = 0

З рівнянь визначити невідомі необхідні опорні реакції R_A і R_B

Виконати перевірку, використовуючи рівняння рівноваги Σ F_iy = 0

Література:

Сетков В.Я. Сборник задач для расчетно-графических работ по технической механике. М.: 1988

ЛЕКЦІЯ № 13

Тема 1.5. Просторові системи сил.

План лекції

1. Загальні відомості.

1.1 Поняття ПСС

1.2 Головний вектор і головний момент ПСС

1.3 Умови та рівняння рівноваги ПСС

2. Поняття моменту сили відносно осі у ПСС.

1. Загальні відомості

Просторовою системою сил називається система сил, лінії дії яких не лежать в одній площині.

Згідно з основною теоремою статики (теоремі Пуансо) будь-яку

довільну систему сил, діючу на тверде тіло, можна

замінити еквівалентною системою, що складається з сили (гловного вектора системи) і пари сил (головного моменту системи сил). Звідси випливає:

Умова рівноваги довільної просторової системи сил

У геометричній формі: R = 0 M_o = 0

для рівноваги довільної просторової системи сил необхідно і достатньо, щоб головний вектор і головний момент системи дорівнювали нулю

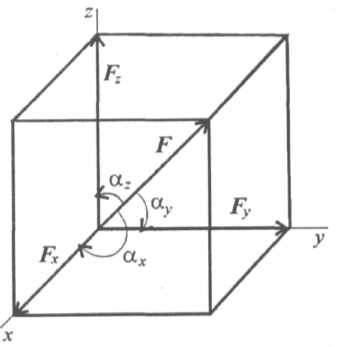
Головний вектор F_гл (R = 0) - геометрична сума всіх сил даної просторової системи сил (модуль головного вектора визначається чеерз проекції на осі х, у, z всіх сил системи).

Головний момент М_ГЛ (Mo = 0) - геометрична сума моментів усіх сил відносно точки приведення.

В аналітичній формі: ΣF_kx = 0 ΣF_ky = 0 ΣF_kz = 0

M_x (F_k) = 0 M_y (F_k) = 0 M_z (F_k) = 0

для рівноваги довільної просторової системи сил необхідно і достатньо, щоб суми проекцій всіх сил на три координатні осі і суми моментів всіх сил щодо цих осей дорівнювали нулю

Три суми проекцій сил на осі координат і три суми моментів щодо осей координат. Шість рівнянь рівноваги для ПСС відповідно незалежним можливим ступенями рухливості тіла в просторі: трьом переміщенням уздовж координатних осей і трьом обертання навколо цих осей.

2. Поняття моменту сили відносно осі у ПСС

Момент сили відносно осі - скалярна величина, що дорівнює моменту проекції цієї сили на площину, перпендикулярну осі, взятому щодо точки перетину осі з площиною.

Момент> 0, якщо дивлячись назустріч осі, ми бачимо поворот, який прагне зробити сила спрямований проти годинникової стрілки (на рис. М> 0).

Момент сили відносно осі дорівнює 0:

1) якщо сила паралельна осі (у цьому випадку Fxy = 0),

2) якщо лінія дії сили перетинає вісь (в цьому випадку h = 0);

тобто момент сили відносно осі дорівнює нулю, якщо вісь і сила лежать в одній площині.

Питання для самоперевірки

1. Яка система сил називається просторової?

2. Назвіть рівняння рівноваги довільної просторової системи сил.

3. Що називається моментом сили відносно осі?

4. У яких випадках момент сили відносно осі дорівнює 0.

Питання для самостійного вивчення:

1. Приведення просторової системи сил

2. Рівняння рівноваги системи паралельних сил у просторі.

Література:

Бычков В.Д. и Миров М.О. Теоретическая механика. с. 85-99

ЛЕКЦІЯ № 14

Тема 1.6 Центр ваги тіла та стійкість рівноваги

План лекції

1. Центр паралельних сил, його властивості.

2. Визначення координат центру паралельних сил.

3. Сила ваги тіла, як центр паралельних сил.

4. Координати центру ваги тіла для об’єму, тонкої однорідної пластини, лінії.

С/Р 5. Координати центру ваги складних фігур.

С/Р 6. Стандартні профілі прокату

1. Центр паралельних сил, його властивості.

Центр ваги - незмінно пов'язана з твердим тілом точка, через яку проходить рівнодійна сил тяжіння, діючих на частки цього тіла при будь-якому положенні тіла в просторі.

У однорідного тіла, що має центр симетрії (круг, куля, куб і т. д.), центр тяжіння знаходиться в центрі симетрії тіла. Положення центру тяжіння твердого тіла співпадає з положенням його центру мас.

Центр паралельних сил

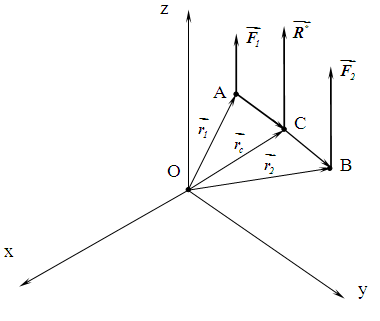
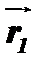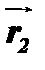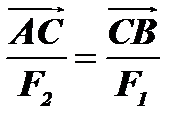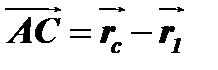Розглянемо паралельні нерівні між собою сили і в системі координат Oxyz, де точки прикладання цих сил А і В визначаються радіусами-векторами і відповідно. Радіус-вектор визначає точку С прикладання рівнодіючої даних сил (рис.1.28). Тоді на підставі рівняння (1.32) можна записати, що . Але і .

Отже:

, звідки: .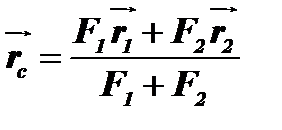

Якщо узагальнити отриманий результат на систему 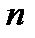паралельних сил , то отримаємо, що:

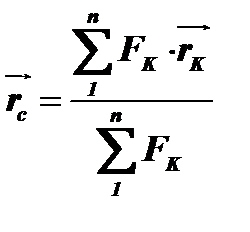
Це рівняння визначає положення центра паралельних сил у векторній формі.

Дата добавления: 2014-12-16