Засоби завдання руху

П р и р о д н и й спосіб полягає в тому, що рух точки задається її траєкторією і рівнянням руху по цієї траєкторії (законом руху)

Рівняння руху в загальному вигляді записується наступним чином:

S = f (t)

де S - відстань точки від початкового положення, що є функцією часу;

t - час руху точки від початкового моменту

Знаючи траєкторію точки і рівняння руху по цій траєкторії, можна визначити положення точки в будь-який момент часу, для чого слід в рівність підставити час.

При своєму русі точка проходить певний шлях, який також є функцією часу. Слід підкреслити, що шлях, пройдений точкою, збігається з відстанню від початку відліку лише тоді коли точка весь час рухається в одному напрямку і початок її руху збігається з початком відліку.

К о о р д и н а т н и й спосіб полягає в тому, що рух точки задається рухом її проекцій уздовж осей координат.

Рівняння плоского руху точки в координатній формі записуються наступним чином

х = f (t) у = f₁ (t)

Знаючи рівняння руху точки в координатній формі, можна, підставивши в ці рівняння час, визначити положення проекцій точки, а отже, і самої точки в будь-який момент часу.

Для того щоб при координатному способі завдання руху точки визначити

рівняння траєкторії у = f (х), необхідно з рівнянь руху виключити час.

Міжнародна система одиниць (СІ) встановлює в якості одиниці довжини

м е т р, а в якості одиниці часу - секунду.

Питання для самоперевірки

1. Кінематика – що це?

2. Завдання кінематики.

3. Назвіть основні поняття кінематики.

4. Що таке механічний рух?

5. Який рух є відносним?

6. Які розподіляють рух в залежності від форми траєкторії?

7. Назвіть способи завдання руху, в чому іх суть.

Питання для самостійного вивчення:

1. Розв’язування задач і визначення параметрів руху.

2. Виконання індивідуальних завдань.

Література:

Тимко И.А. Теоретическая механіка. Издательство Харьковского университета. Харьков, 1971, с.207-211

ЛЕКЦІЯ № 20

Тема 2.1 Кінематика. Основні поняття кінематики.

План лекції

1. Види руху точки по заданій траєкторії в залежності від її прискорення.

2. Визначення параметрів руху точки по заданій траєкторії для будь-якого виду руху.

3. Поступальний рух твердого тіла.

4. Оберти тіла навкруг непорушної осі.

1. Види руху точки по заданій траєкторії в залежності від її прискорення.

Прискорення - це зміна швидкості. У будь-якій точці траєкторії

прискорення задається не тільки зміною абсолютного значення швидкості, а й її напрямку. Прискорення визначається як границя відношенні приросту швидкості до інтервалу часу, за який цей приріст відбувся.

Види руху:

Рівномірний рух – це рух тіла, при якому прискорення не змінюється ні за величиною, ні за напрямком.

Нерівномірний рух - якщо точка в рівні проміжки часу проходить нерівні шляхи.

Рівномірно-змінний рух – рух, при якому за рівні проміжки часу швидкість змінюється на одну і ту ж величину.

2.Визначення параметрів руху точки по заданій траєкторії для будь-якого виду руху

Координатний спосіб завдання руху точки

Положення в просторі рухомої точки визначається трьома координатами в декартовій системі координат. Ці координати задаються як функції часу:

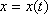
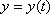
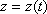(1)

Залежності (1) називаються рівняннями руху точки в декартових координатах.

Якщо рух точки відбувається в площині ХУ, то задаються тільки два рівняння руху: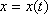

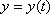
При прямолінійному русі точки досить задати одне рівняння руху: 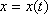, якщо прийняти, що вісь х збігається з прямою, по якій рухається точка.

Швидкість точки являє собою вектор, що характеризує швидкість і напрям руху точки в даний момент часу.

При завданні руху точки рівняннями (1) проекції швидкості на осі декартових координат дорівнюють:

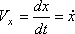
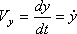
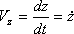
Модуль швидкості

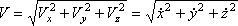(2)

Напрямок швидкості визначається напрямними косинусами:

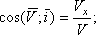
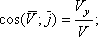
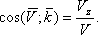
Якщо рух точки задається в площині ХУ, то;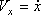

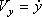
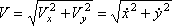
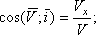
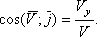
При прямолінійному русі по осі х: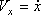

Характеристикою швидкості зміни швидкості є прискорення а. Прискорення точки одно похідною від вектора швидкості по часу:

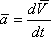
При завданні руху точки рівняннями (1) проекції прискорення на координатні осі дорівнюють:

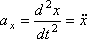
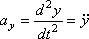
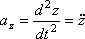
Модуль прискорення:

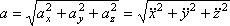(3)

Напрямок прискорення визначається напрямними косинусами

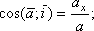
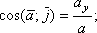
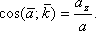
Якщо рух точки задається в площині ХУ, то: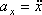

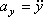
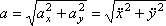
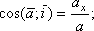
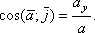
При прямолінійному русі по осі Х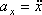

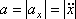
Природний спосіб завдання руху точки:

Вважається, що рух точки задано природним способом, якщо вказані її траєкторія і закон зміни криволінійної координати. Рівняння називається 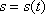законом руху точки по траєкторії. При цьому на траєкторії вказується початок відліку, а також позитивний напрямок відліку координати s у вигляді стрілки .

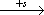Модуль швидкості точки визначається за формулою

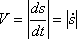
Вектор швидкості V спрямований по дотичній до траєкторії в бік стрілки 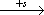, якщо 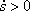, і в протилежну сторону, якщо .

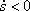Прискорення точки визначається як векторна сума дотичного і нормального прискорень точки: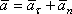

Модуль дотичного прискорення визначається за формулою

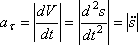
Вектор дотичного прискорення направлений по дотичній до траєкторії в бік стрілки 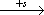, якщо 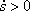, і в протилежну, якщо .

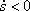Модуль нормального прискорення визначається за формулою

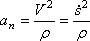
де - ρ радіус кривизни траєкторії в даній точці.

Вектор нормального прискорення 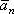завжди спрямований по головній нормалі в бік центру кривизни траєкторії.

Модуль повного прискорення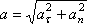

2. Поступальний рух твердого тіла

Тверде тіло – це система матеріальних точок, відстані між якими незмінні.

Поступальним рухом (спрямований вперед) твердого тіла називають такий рух, при якому будь-яка лінія, що з’єднує дві довільні точки тіла, зберігає незмінною свою орієнтацію в просторі.

При поступальному русі:

• всі точки тіла описують однакові (дискантні, конгруентні) траєкторії;
• швидкості усіх його точок однакові в даний момент часу;
• прискорення усіх його точок однакові в даний момент часу;

Поступальний рух твердого тіла повністю визначається рухом будь – якої однієї його точки, тобто кінематика поступального руху може бути зведена до кінематики точки.

3. Оберти тіла навкруг непорушної осі

Рух, траєкторія якого крива лінія, називають криволінійним. Наприклад, рух по колу, еліпсу, параболі, гіперболі. Обертальний рух тіла навколо осі – це рух, при якому траєкторією руху усіх його точок є кола з центром, що лежать на одній прямій, яка називається віссю обертання. Миттєва швидкість направлена по дотичній до траєкторії (завжди перпендикулярна до радіуса). Рух тіла по коловій траєкторії є окремим випадком криволінійного руху. Такий рух завжди буде прискореним, оскільки швидкість буде змінюватись за напрямком. Тому тіло має нормальне прискорення, яке напрямлене перпендикулярно до швидкості в даній точці, тобто вздовж радіуса кривизни траєкторії. Якщо змінюється й модуль швидкості, то тіло також має і тангенціальне прискорення

Повне прискорення 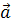матеріальної точки дорівнює векторній сумі її тангенціального і нормального прискорення: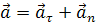

Модуль прискорення точки: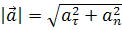

Напрямок повного прискорення визначається кутом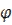

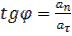
Зміну положення матеріальної точки під час руху по колу характеризують довжиною дуги або кутом повороту. Кут повороту (кутове переміщення) 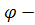скалярна фізична величина, яка характеризує зміну положення тіла в просторі при обертальному русі і вимірюється кутом повороту радіуса, який проведено від осі обертання до певної точки тіла, що обертається. Одиниця кута в СІ – радіан:

Частота обертання n – скалярна фізична величина, яка характеризує швидкість обертального руху і вимірюється відношенням кількості обертів до інтервалу часу, протягом якого вони здійснені.

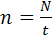
Одиниця частоти обертання в СІ – герц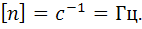

Час одного оберта називається періодом: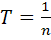

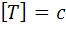
Модуль лінійної швидкості матеріальної точки при рівномірному русі по колу:

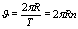
R - радіус кола.

Кутова швидкість 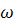- кут повороту радіуса, проведеного до певної точки тіла, що обертається за одну секунду:

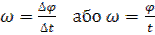
Одиниця кутової швидкості в СІ – радіан за секунду

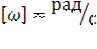
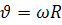
Модуль кутової швидкості при рівноприскореному русі тіла по колу:

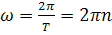
При рівномірному русі по колу тіло має тільки нормальне прискорення, яке завжди напрямлене до центра кола по радіусу і називається доцентровим прискоренням:

a = .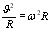

Питання для самоперевірки

8. Кінематика – що це?

9. Завдання кінематики.

10. Назвіть основні поняття кінематики.

11. Що таке механічний рух?

12. Який рух є відносним?

13. Які розподіляють рух в залежності від форми траєкторії?

14. Назвіть способи завдання руху, в чому іх суть.

15. Назвіть види руху

16. Охарактеризуйте природний та координатний спосіб завдання руху точки

17. Що називається поступальним рухом?

18. Основні формули при оберті тіла навкруг непорушної осі.

Питання для самостійного вивчення:

1. Виконання індивідуальних завдань.

Література:

Тимко И.А. Теоретическая механіка. Издательство Харьковского университета. Харьков, 1971, с. 223-238

Бычков Д.В. и Миров М.О. Теоретическая механика, 1976. с.127-1

ЛЕКЦІЯ № 21

Тема 2.1 Динаміка.

Основні поняття, аксіоми і загальні теорії динаміки.

План лекції

1. Основні поняття динаміки

2. Основні аксіоми динаміки

3. Метод кінетостатики

4. Загальні теореми динаміки

Дина́міка - розділ механіки, що вивчає закони руху тіл під дією прикладених до них сил.

Основні поняття: маса, сила, імпульс, енергія.

Динамічний аналіз використовується для визначення дії на конструкцію або її складові частини навантажень, що залежать від часу.

Прикладами таких навантажень являються:

· циклічні навантаження (обертові частини устаткування);

· раптово прикладені навантаження (удар або вибух);

· випадкові навантаження (землетрус);

· будь-які інші змінні навантаження

Задачі динаміки:

1) Пряма задача динаміки полягає в тому, щоб по заданому руху матеріальної точки визначити сили, що діють на неї. Для її вирішення перш за все необхідно визначити прискорення точки з умов кінематики. Визначивши прискорення точки, потрібно потім скористатися основним законом динаміки і знайти діючу силу. Якщо на точку діє декілька сил і невідомі лише деякі з них, то для їх визначення доводиться використовувати аксіому незалежності дії сил.

2) Зворотня задача динаміки полягає в тому, щоб по заданих силам визначити рух точки. Тут також доводиться використовувати основний закон динаміки. З цього закону прискорення визначається через діючу силу і задану масу точки.

Для розв’язання задач динаміки застосовуються два основних способи:

· статичний, оснований на застосуванні рівнянь динамічної рівноваги, які відрізняються від рівнянь статичної рівноваги додатковим врахуванням сил інерції у вигляді добутку мас або їхніх моментів інерції на прискорення;

· енергетичний, оснований на застосуванні закону збереження енергії, відповідно до якого сума потенційної й кінетичної енергії пружної системи є величина постійна.

2.Аксіоми динаміки

1 Перша аксіома динаміки - закон інерції - пояснює, що рівномірний і прямолінійний рух точки або тіла відбувається лише в тому випадку, якщо на точку (тіло) діє врівноважена система сил. І навпаки, якщо потрібно, щоб точка або тіло рухалися рівномірно і прямолінійно, то необхідно створити умови для рівноваги всіх сил, прикладених до даного пункту або до даного тіла.

2 Друга аксіома динаміки - основная аксиома динамики - основний закон динаміки точки F = ma.

Цей закон стверджує, по-перше, що причиною прискорення служить сила, по-друге, що числове значення придбаного точкою прискорення пропорційно числовому значенню сили і, по-третє, що напрямок вектора прискорення завжди збігається з напрямком вектора сили.

3 Третя аксіома динаміки - закон рівності дії і протидії - в задачах по динаміці, так само як і в статиці, використовується при визначенні взаємодії рухаються тел.

4 Четверта аксіома динаміки - закон незалежності дії сил - дозволяє при вирішенні задач динаміки вибирати шляхи їх вирішення. Якщо на матеріальну точку діє декілька сил, то можна знайти їх рівнодіючу, а потім розглянути її дія на точку - знайти прискорення точки, але можна спочатку знайти прискорення, придбані від дії кожної сили окремо, а потім ці прискорення геометрично скласти.

• Метод кінетостатики

Принцип Даламбера і заснований на ньому метод кінетостатікі встановлюють єдиний підхід до дослідження руху невільної матеріальної точки і невільною матеріальної системи незалежно від виду зв'язків, що накладаються на їх рух. Цей підхід полягає в доданні динамічним рівнянням виду рівнянь рівноваги або виду рівнянь статики, що дозволяє при вирішенні задач динаміки застосовувати прості і наочні прийоми і методи статики.
принцип Даламбера для матеріальної точки: у кожен момент руху матеріальної точки активні сили, реакції зв'язків та сила інерції утворюють врівноважену систему сил.
принцип Даламбера для системи матеріальних точок: якщо до активних силам (зовнішнім і внутрішнім) і реакцій зв'язків (зовнішніх і внутрішніх), чинним на кожну матеріальну точку системи, додати силу інерції точки, то в будь-яку мить часу отримана система сил буде врівноваженою.
Таким чином, наслідки з принципу Даламбера для системи матеріальних точок можна сформулювати так: при русі системи матеріальних точок геометрична сума головних векторів зовнішніх активних сил, реакцій зовнішніх зв'язків і сил інерції системи, а також геометрична сума головних моментів вказаних сил щодо довільного центру дорівнюють нулю в будь-яку мить часу.

Питання для самоперевірки

1. Що таке динаміка, і її основні задачі

2. Способи розв’язання задач динаміки

3. Аксіоми динаміки

4. В чому принцип методу кінетостатики?

Література:

Бычков Д.В. и Миров М.О. Теоретическая механика, 1976. с.186-190

Тимко И.А. Теоретическая механіка. Издательство Харьковского университета. Харьков, 1971, с.239-253

Дата добавления: 2014-12-16