Визначення координат центру паралельних сил

Координати центра паралельних сил обчислюють через проекції радіуса-вектора 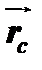на осі координат:

x_с = Σ (G_i x_i) / ΣG_i

y_с = Σ (G_i y_i) / ΣG_i

z_с = Σ (G_i z_i) / ΣG_i

G_i –сила тяжіння кожної елементарної частка тіла

x_i , y_i , z_i - координати частки

ΣG_i - сила тяжіння всього тіла

3. Сила ваги тіла, як центр паралельних сил.

Сила з якою тіло притягується до землі, називається силою тяжіння.

Центром ваги тіла називають центр системи паралельних сил, яку наближено утворюють сили ваги його елементарних частинок.

Центр тяжіння є геометрична точка, яка може лежати поза тілом (наприклад, кільце, циліндр з отвором).

4. Координати центру ваги тіла для об’єму, тонкої однорідної пластини, лінії.

Для об’єму: x_с = Σ (V_i x_i) / Σ V_i

Для площі тонкої однорідної пластини: x_с = Σ (F_i x_i) / Σ F_i

Для лінії: x_с = Σ (l_i x_i) / Σl_i

5. Координати центру ваги складних фігур.

1) Центр тяжіння дуги кола. Розглянемо дугу АВ радіусу R з центральним кутом. В силу сімметрії центр тяжіння цієї дуги лежить на осі Ox

Знайдемо координату Хс по формулі .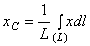

Для цього виділимо на дузі АВ елемент ММ' завдовжки , положення якого визначається кутом 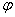. Координата х елементу ММ' буде . Підставляючи ці значення х і 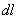і маючи на увазі, що інтеграл має бути поширений на всю довжину дуги, отримаємо:

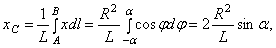
где L - длина дуги АВ, равная 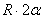. Отсюда окончательно нахо­дим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном

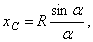
де кут вимірюється в радіанах.

2) Центр тяжіння площі трикутника. Розіб'ємо площу трикутника

ABD прямими, паралельними AD, на вузькі смужки; центри тяжіння цих смужок лежатимуть на медіані BE трикутника.

Отже, і центр тяжіння усього трикутника лежить на цій медіані.

Аналогічний результат виходить для двох інших медіан. Звідси робимо висновок, що центр тяжіння площі трикутника лежить в точці перетину його медіан.
При цьому, як відомо

3) Центр тяжіння площі кругового сектора. Розглянемо круговий

сектор ОАВ радіусу R з центральним кутом. Розіб'ємо подумки площу сектора ОАВ радіусами, проведеними з центру О, на п секторів. У межі, при необмеженому збільшенні числа, ці сектори можна розглядати як плоскі трикутники, центри тяжіння яких лежать на дузі DE радіусу. Отже, центр тяжіння сектора ОAB буде зівпадати з центром тяжіння дуги DE. Остаточно отримаємо, що центр тяжіння площі кругового сектора лежить на його центральній осі симетрії на відстані від початкового центру О, дорівнює

6. Стандартні профілі прокату

Профіль - це форма поперечного перерізу прокатного виробу.

Сортамент - це сукупність прокатних профілів що відрізняються за формою і розмірам.

В сортаменті вказано: перелік прокатних профілів з вказівкою форми, геометричних характеристик, маси одиниці довжини, допусків і умов постачання. Різноманітність видів профілів, що входять в сортамент, а також досить часта градація розмірів одного виду профілю забезпечують економічне проектування конструкцій при нагоді створення різноманітних конструктивних форм.

Стандартні профілі прокату: куткові профілі, двутавр, швелер.

Куткові профілі

Куткові профілі прокатують у вигляді равнополочных (ГОСТ 8509-72) і нерівнополочних (ГОСТ 8510-72) куточків. Сортамент куточків дуже великий: від дуже малих профілів з площі перерізу 1-1,5 см2 до потужних профілів з площею перерізу 140 см2. Полиці куточків мають паралельні грані, що полегшує конструювання. Широке застосування куточки мають в легких наскрізних конструкціях. Робочі стержні з куточків зазвичай компонуються в симетричні перерізи з двох або чотирьох куточків. Економічніші куточки з меншою товщиною полиць. У стислих стержнях перерізи, складені з тонких куточків, мають більшу стійкість. У стержнях з отворами для болтів послаблення перерізу отворами тим менше, чим тонше.

Двутаври

Двутаври - основний балочний профіль - має найбільшу різноманітність по типах, які відповідають певним сферам застосування.

Балки двотаврові звичайні (ГОСТ 8239-72) мають ухил внутрішніх граней полиць і позначаються номером, що відповідає їх висоті в сантиметрах. У сортамент входять профілі від № 10 до № 60. Стінки у великих двутавров мають мінімальну товщину, за умовами стійкості досягають 1/55 висот двутавра. Чим тонше стінка, тим вигідніше переріз балки при роботі її на вигин. Проте за умовами технології плющення у більшості двутавров стінки виходять значно товще, ніж це потрібно по умові їх стійкості. Завдяки зосередженню матеріалу в полицях двутаври мають велику жорсткість відносно осі х, але невелика ширина полиць робить їх малостійкими відносно осі у. Двутаври застосовуються в елементах (балках), що згинаються, а також в гілках колон і різних опор, де для їх стійкості застосовуються складені перерізи.

Балки двотаврові широкополочні мають паралельні грані полиць. Широкополочні двутаври прокатуються трьох типів: нормальні двутаври (Б), широкополочні двутаври (Ш), колонні двутаври (К). Висота балочних профілів (Б) і (Ш) досягає 1000мм при відношенні ширини полиць до висоти від b: h = 1: 1,65 (при малих висотах) до b: h = 1: 1,25 (при великих висотах). Колонні профілі (К) мають відношення ширини полиць до висоти, близьке 1:1, що надає їм стійкість відносно осі у.
Конструктивних переваги (паралельність граней полиць і потужність перерізів) дозволяють застосовувати широкополочні двутаври у вигляді самостійного елементу (балки, колони, стержні важких ферм), що не вимагає майже ніякої обробки, що знижує трудомісткість виготовлення конструкцій в 2-3 рази.

З широкополочних двутаврів шляхом розрізання полиці в подовжньому напрямі отримують таврові профілі, зручні для застосування в рішотчастих конструкціях. У міру розширення виробництва широкополочних двутавров застосування звичайних двутаврів скорочується.
Розвиток автоматичного зварювання створює сприятливі умови для виробництва зварних двутаврів з універсальної сталі по певному сортаменту, що дає можливість користуватися ними так само, як і прокатними.

Швелери

Геометричних характеристики перерізу швелерів визначаються його номером, який відповідає висоті стінки швелера (у сантиметрах). Сортамент (ГОСТ 8240-72) включає швелери від № 5 до № 40 з ухилом внутрішніх граней полиць. Ухил внутрішніх граней полиць утрудняє конструювання. У ГОСТ входять і швелери з паралельними гранями полиць, переріз яких має кращі розрахункові характеристики відносно осей х і у і конструктивніші, оскільки спрощують болтові кріплення до полиць. Швелери застосовуються в потужних стержневих конструкціях (мостах, великопрольотних фермах і т. п.), а також в колонах, зв'язках і покрівельних прогонах.
Стержні зі швелерів, працюючі на осьову силу, компонуються в жорсткі відносно осей х і у симетричні перерізи.

Питання для самоперевірки

1. Що називають центром ваги?

2. Положення центру тяжіння твердого тіла.

3. Як обчислюють координати центра паралельних сил?

4. Що називається силою тяжіння?

5. За визначають координати центру ваги тіла для об’єму, тонкої однорідної пластини, лінії.

6. Координати центру ваги складних фігур.

7. Що таке сортамент?

8. Назвіть основні прокатні профілі, та їх характеристику.

Питання для самостійного вивчення:

1. Стандартні профілі прокату

Література:

Бычков Д.В., Миров И.О. Теоретическая механика, М.: Высш. школа 1976 с.101-108

Техническая механика. Учебник для техникумов / Эрдеди А.А., Аникин И.В., Медведев Ю.А. – М.: Высш.школа, 1980 - с. 61- 68

Сортамент прокатних профілів

ЛЕКЦІЯ № 15

Тема 1.6 Центр ваги. Методика розв’язання задач.

Визначення положення центру ваги перерізів

План лекції

1. Координати центру тяжіння тіла.

2. Методика рішення задач.

3. Приклад задачі

1. Теоретичне обґрунтування

Центром тяжіння тіла називають точку всередині тіла (або поза ним), відносно якої сума моментів сил тяжіння, які діють на окремі частини тіла, дорівнює нулю.

Положення центра тяжіння будь-якого тіла можна знайти, розбиваючи тіло на частини більш простої форми і визначаючи центри прикладання рівнодійної сил тяжіння, які діють на ці частини. Наприклад. тонка однорідна пластинка

Розіб'ємо пластинку на багато малих рівних між собою смужок. На кожну з них діє сила тяжіння - всі ці сили рівні між собою. Складаємо по дві сили, рівновіддалені від середини смужок. Рівнодійні будь-яких двох таких сил прикладено в середині смужки. Звідси випливає, що центр тяжіння однорідної тонкої пластинки знаходиться в її середині. Так само можна встановити, що центр тяжіння однорідного прямокутного стрижня знаходиться в його середині (рис.2.2.42), трикутника - в точці перетину його медіан (рис.2.2.43), паралелограма - в точці перетину його діагоналей (рис.2.2.44), однорідного кільця - в його геометричному центрі (рис.2.2.45)

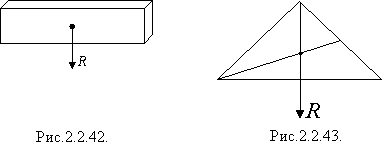
Наведені приклади доводять, що якщо тіло має центр симетрії, то центр тяжіння збігається з центром симетрії. Якщо тіло має вісь симетрії, то його центр тяжіння лежить на цій осі. Якщо тіло має площину симетрії, то його центр тяжіння лежить в цій площині.

В будь-якій точці фізичного тіла діє сила тяжіння. Через невеликі розміри тіл, що розглядаються, у порівнянні з відстанню їх до центру Землі, сили тяжіння розглядають як систему паралельних сил. Рівнодіючу сил тяжіння точок тіла називають силою тяжіння, а точку її прикладання – центром тяжіння (або центром ваги тіла)

Координати центру тяжіння тіла визначають за формулами:

;

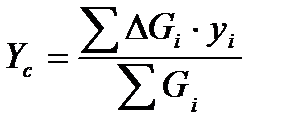
Координати центру тяжіння тіла, що складається з площин, визначають за формулами:

;

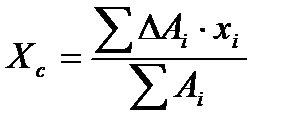Добуток площі тіла на відстань від центра тяжіння цього тіла до осі зветься статичним моментом тіла відносно осі

;

2. Методика розв’язання задач.

Визначення положення центра ваги складного перерізу (використовувати таблиці сортаменту прокатних профілів).

1. Розбиваємо переріз на профілі прокату, позначаємо цифрами 1,2,3,..n

2. Вказуємо центри ваги кожного профілю С1, С2,С3,…n

3. Обираємо систему координатних осей.

Усі перерізи мають одну вісь перерізу, тому рекомендується одну з координатних осей сполучати з нею. Другу вісь координат направляють перпендикулярно першій так, щоб вона перетинала центри тяжіння однієї з фігур. Другу вісь можливо направити так, щоб вона пройшла крізь нижню (крайню) точку перерізу. В першому випадку рішення будуть більш простими.

4. Визначаємо з відповідних таблиць сортаменту площі профілів А1, А2, А3,...n і, використовуючи розміри, знаходимо координати їхніх центрів ваги х1, х2, х3, …n і у1,у2, у3,…n відносно обраних осей координат (координати у_с = 0, тому що вісь X збігається з віссю симетрії). По черзі для кожного профілю: відстань від 0 центральних вісей до центру вісей С1, потім від 0 до С2, і т.д. відстань відповідно осі Х – відстані Х1, Х2, Х3,…n.

5. Визначаємо повну площу перетину А (сума всіх А1,А2,А3…n) (см²)

6. Знаходимо статичний момент перетину S_y = А₁х₁+А₂х₂+А₃х₃+А₄х₄ (см³)

S_х = А₁у₁+А₂у₂+А₃у₃+А₄у₄(см³)

Якщо вісь X збігається з віссю симетрії, S_х = 0,

7. Визначаємо координати центра ваги

х_с =S_у/A

у_с =S_х/A

Якщо вісь X збігається з віссю симетрії, то координата у_с = 0

8. Отже точка С має координати (х_с; y_с)

Наносимо знайдений центр ваги на малюнок перерізу.

Дата добавления: 2014-12-16