Введение. Право-линейная и автоматная грамматики

Теория автоматов

Право-линейная и автоматная грамматики

Определение. Грамматика называется право -линейной, если правая часть каждого правила содержит не более одного нетерминала, причем он является самым правым символом.

Правила право линейной грамматики имеют вид:

A ® w B, A ® w, w Î V*, B Î W.

Определение. Грамматика называется автоматной, если ее правила имеют вид:

A ® x B, A ® x, A ® e, x Î V, B ÎW.

Синтез конечных автоматов, распознающих язык, порождаемый грамматикой, предусматривает, что такая грамматика должна быть автоматной.

Пример. Преобразовать грамматику, заданную правилами вида:

1. S ® a A 4. A ® a b b S

2. S ® b c 5. A ® c A

3. S ® A 6. A ® e

к автоматной.

Решение. Последовательно будем вводить новые нетерминалы в

тех правилах, где необходимо обозначить цепочку нетерминалов и терминалов или одних терминалов одним символом. Новые правила примут вид:

1. S ® a A 6. S ® e

2. S ® b К1 7. A ® a K2

3. K1 ® c 8. K2 ® b K3

4. S ® a K2 9. K3 ® b S

5. S ® c A 10. A ® c A

12. A ® e

Теория автоматов лежит в основе теории построения компиляторов. Конечный автомат - одно из основных понятий. Под автоматом подразумевается не реально существующее техническое устройство, хотя такое устройство может быть построено, а некоторая математическая модель, свойства и поведение которой можно имитировать с помощью программы на вычислительной машине. Конечный автомат является простейшей из моделей теории автоматов и служит управляющим устройством для всех остальных видов автоматов. Конечный автомат обладает рядом свойств:

· конечный автомат может решать ряд легких задач компиляции. Лексический блок почти всегда строится на основе конечного автомата.

· работа конечного автомата отличается высоким быстродействием.

· моделирование конечного автомата требует фиксированного объема памяти, что упрощает проблемы, связанные с управлением памятью.

· существует ряд теорем и алгоритмов, позволяющих конструировать и упрощать конечные автоматы.

В литературе существует несколько отличных определений конечного автомата. Однако, общим в них является то, что конечный автомат моделирует вычислительное устройство с фиксированным объемом памяти, которое читает последовательности входных символов, принадлежащие некоторому входному множеству. Принципиальные различия в определениях связаны с тем, что автомат делает на выходе. Выходом автомата может быть указание на то «допустима» или нет данная входная цепочка. «Допустимой» называется правильно построенная или синтаксически правильная цепочка. Например, цепочка, которая должна изображать числовую константу, считается построенной неправильно, если она содержит две десятичные точки.

Определение. Конечный автомат - это формальная система, которая задается с помощью следующих объектов [3]:

· конечным множеством входных символов;

· конечным множеством состояний;

· функцией переходов, которая каждой паре (текущее состояние, входной символ) ставит в соответствие новое состояние;

· начальным состоянием;

· подмножеством состояний, выделенных в качестве допускающих или заключительных.

Пример. Разберем работу контроллера, проверяющего четно или нечетно число единиц в произвольной цепочке, состоящей из нулей и единиц. Соответствующий конечный автомат должен «допускать» все цепочки, содержащие нечетное число единиц и «отвергать» цепочки с четным их числом. Назовем этот автомат «контроллером четности». Считаем, что символы, отличные от 0 и 1 нельзя подавать на вход автомата.

Итак, входной алфавит контроллера есть множество {0, 1}. Считаем, что в конкретный момент времени конечный автомат имеет дело лишь с одним входным символом, а информацию о предыдущих символах входной цепочки сохраняет с помощью конечного множества состояний. В качестве множества состояний будем рассматривать множество { чет, нечет }, одно из этих состояний должно быть выбрано в качестве начального. Пусть им будет состояние {чет}, поскольку на первом шаге число прочитанных единиц равно нулю, а нуль есть четное число. При чтении очередного входного символа состояние автомата меняется, причем новое его состояние зависит от входного символа и текущего состояния. Такое изменение состояния называется переходом. Может оказаться, что новое состояние совпадает со старым.

Работа автомата может описываться математически функцией переходов вида d(Sтек., x) = Sнов. Иначе это можно записать следующим образом:

d(чет., 0)= чет. d(чет., 1)= нечет.

d(нечет., 0) = нечет. d(нечет., 1) = чет.

Контроллер имеет единственное допускающее состояние НЕЧЕТ, а ЧЕТ есть «отвергающее» состояние. Отразим последовательность переходов автомата при подаче на его вход цепочки 1101.

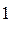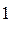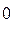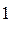ЧЕТ ® НЕЧЕТ ® ЧЕТ® ЧЕТ® НЕЧЕТ

Таблица переходов такого автомата имеет вид:

чет	чет	нечет
нечет	нечет	чет

Определение. Конечный автомат - это формальная система

S = { A, Q, d, l,V },

объекты которой следующие:

A - конечное множество входных символов (множество терминалов);

Q - конечное множество внутренних состояний автомата (множество

нетерминалов);

V - конечное множество выходных символов (выходной алфавит);

d - функция переходов автомата из одного состояния в другое, для которой

характерно A ´ Q ® Q;

l - функция выходов, определяющая отображение вида:

A ´ Q ® V.

Дата добавления: 2014-12-16