Способы представления конечных автоматов

Конечный автомат можно представлять несколькими способами:

- ориентированным графом (графом состояний), в котором

состояния есть вершины графа, а дуги есть переходы между

состояниями:

a₃,V₃

q₂ q₄

a₁,V₁

a₅,V₆

q₁

a₃,V₅

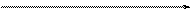
a2,V₂ q3 q5 q6

a4,V₄ a7,V8

a_i - символы входного алфавита, вызывающие переходы; V_i - символы выходного алфавита; q_i - состояния автомата.

- таблицей переходов, в которой по строкам располагаются

состояния автомата, а по столбцам - символы входного алфавита. Клетки таблицы заполняют состояния, в которые переходит автомат под действием входных символов, а также символы выходного алфавита, соответствующие реакции автомата на входной символ. Например,

	a1	a2	a3	a4	a5	a6
q1 начальное состояние	q2, V1	q3, V2
q2			q4, V3
q3				q5, V4
q4			q5, V5		q5, V6
q5						q6, V7
q6 конечное состояние

- матрицей переходов, которая представляет собой квадратную

матрицу, строки и столбцы которой соответствуют внутренним состояниям автомата. Клетки матрицы заполняются входными символами a_k,при которых автомат переходит из состояния q_i в состояние q_j, а также выходными символами, соответствующими паре (ak, qi). Например,

	q1	q2	q3	q4	q5	q6
q1 начальное состояние		a1, V1	a2, V2
q2				a3, V3
q3					a4, V4
q4					a3, V5 a5, V6
q5						a6, V7
q6 конечное состояние

Определение. Детерминированным конечным автоматом называется такой автомат, каждая клетка таблицы переходов которого не содержит состояний больше одного. В противном случае автомат называется недетерминированным.

Определение. Конечный автомат называется полностью определенным, если его таблица переходов не содержит пустых клеток. Иначе автомат называют частично определенным.

Процедура приведения недетерминированного автомата

к детерминированному виду

1. В таблице переходов определяется клетка, в которой содержится более чем одно состояние, например, q_i и q_j.

2. Строка i и строка j накладываются друг на друга, и в таблице переходов появляется новая «склеенная» строка.

3. Если состояние q_i или q_j присутствует еще в какой-либо клетке таблицы переходов, то соответствующая строка i или j сохраняется в таблице, иначе удаляется после «склеивания».

Переход от не полностью определенного (частично определенного) автомата к полностью определенному в некоторых случаях может осуществляться заданием состояния ошибки, которое вносится во все пустые клетки таблицы.

Понятие изоморфизма двух автоматов

Пусть заданы два автомата:

S_T ={ A_T, Q_T, d _T, l _T, V_T}, S_R={ A_R, Q_R, d _R, l _R,V_R}.

Определение. Автоматы S_T и S_R изоморфны, если элементы множеств входных символов, выходных символов, состояний одного автомата можно переименовать так, что таблицы их переходов совпадут.

Определение. Пусть S_T и S_R - два автомата с одинаковыми входными и выходными алфавитами. Состояния q_T и q_R называются эквивалентными, если для любого a, где a - входной символ, справедливы равенства

l_T (q_T, a) = l_R (q_R, a), d_T (q_T, a) = d_R (q_R, a).

Определение. Состояние q’Î Q_T и q’’Î Q_R называются псевдо эквивалентными, если область определения q’ и q’’ одна и та же и в этой области q’ и q’’ эквивалентны.

Определение. Автоматы S_T и S_R называются псевдо эквивалентными, если для любого состояния автомата S_T найдется псевдо эквивалентное состояние автомата S_R и наоборот.

Замечание. Для полностью определенных автоматов отношение псевдо эквивалентности будет являться отношением эквивалентности.

Пример. Дляавтомата, заданного следующей таблицей переходов

	a1	a2	a3
q1	2,0	-	3,-
q2	-	1,-	3,0
q3	2,1	1,-	3,0

определить наличие эквивалентных и псевдо эквивалентных состояний.

Решение. Рассмотрим состояния q₂ и q ₃ . Область определения для q₂ принадлежит области определения q₃. Кроме того на всей области определения q₂ для " a имеют место равенства

l(q₂, a) @ l(q₃, a), d (q₂, a) @ d (q₃, a),

где ‘ @ ‘ - знак псевдоэквивалентности.

Состояние q₃ может обрабатывать больше входных символов, чем состояние q₂. Поэтому, если в автомате состояние q₂ заменить состоянием q_3, и переход в q₂ заменить на переход в q₃, то получим автомат с большими возможностями, чем предыдущий. В таком случае говорят, что q₃ покрывает состояние q₂.

Определение. Автомат S_T покрывает автомат S_R, если для " q_i Î Q_R найдется состояние q_i Î Q_T, покрывающее его.

Переход от автомата к покрывающему его автомату нельзя назвать эквивалентным преобразованием.

Дата добавления: 2014-12-16