Поверхні обертання

Поверхню, утворену обертанням твірної лінії навколо нерухомої прямої — осі, називають поверхнею обертання.

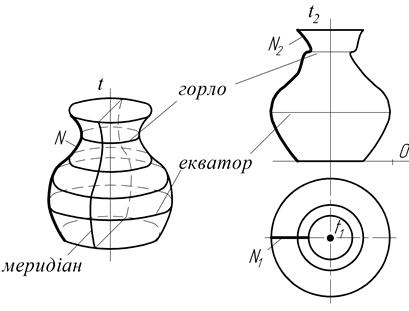На рис. 3.10 зображено поверхню обертання, яка утворена обертанням будь-якої кривої N(N₁,N₂) навколо осі. Найменшу паралель поверхні називають горлом, а найбільшу — екватором.

а) б)

Рисунок 3.10 — Поверхня обертання довільного вигляду

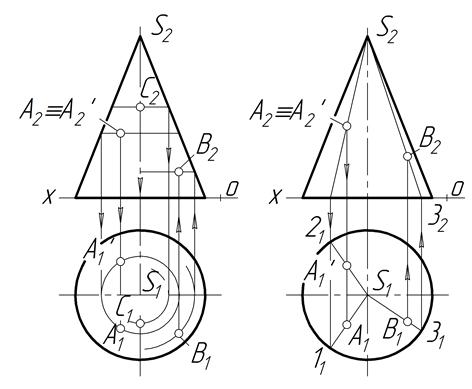
Положення точок на кривій поверхні, подібно до положення точок на гранній поверхні, визначаються за допомогою ліній — прямих або кривих, які проходять через ці точки на заданій поверхні (рис. 3.11).

а) б)

Рисунок 3.11

При перерізі циліндра площиною, в загальному випадку утворюється крива лінія, побудова якої зводиться до пошуку точок перетину твірних поверхні зі січною площиною і сполучення цих точок плавною кривою лінією.

Залежно від положення січної площини відносні осі циліндра у перерізі можуть утворитися кола, еліпси, а також чотирикутники. На рисунку 3.12 показано прямий коловий циліндр перерізаний площинами Σ, α, j.

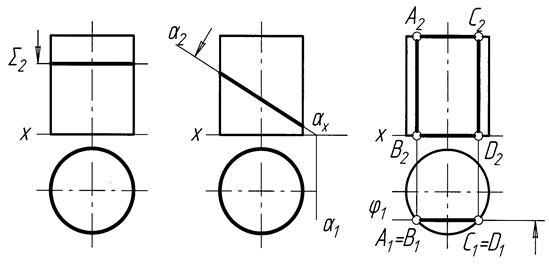
а) коло б) еліпс в) чотирикутник

Рисунок 3.12 – Переріз прямого колового циліндра площиною

Рисунок 3.13— Переріз конуса площиною(конічні перерізи)

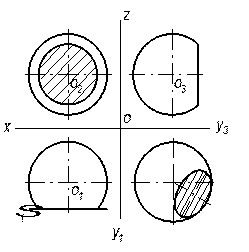
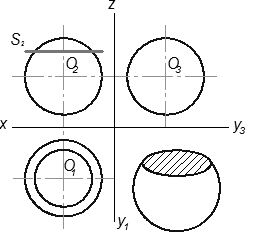Лінією перетину кулі з площиною завжди буде коло. На рисунку 3.14 наведені приклади побудови проекції кіл, які отримані в перетині кулі з площинами, паралельними площинам проекції: горизонтальною (рис.3.14,а), фронтальною (рис.3.14,б) і профільною (рис.3.14,в).

b₁ a₁ j₁

Рисунок 3.15 — Перетин кулі горизонтально-проекційною площиною

При перетині кулі горизонтально-проекційною площиною (рис.3.15), горизонтальна проекція шуканої лінії перетину є відрізок 1-10, який співпадає з горизонтальним слідом площини S. Точки 1 і 10 лежать на головному екваторі кулі. Їх фронтальні проекції 1₂ і 10₂ будуються за горизонтальними проекціями і будуть кінцями малої осі еліпса. Аналогічно знайдемо фронтальні проекції 4₂ і 5₂ точок 4 і 5 еліпса, які лежать на головному меридіані сфери і служать границею видимості еліпса на фронтальній площині проекції. Для того, щоб знайти велику вісь еліпса, необхідно насамперед відшукати центр еліпса. Для цього опускаємо з точки О_с перпендикуляр до сліду S_{1 .} Велика вісь еліпса на площині проекції p₁ проектується у точку 6₁=7₁, яка збігається з центром еліпса S₁

З розглянутих вище прикладів очевидний висновок, що загальним принципом розв’язування задач на перетин поверхонь площиною є застосування допоміжних січних площин.

Загальний порядок розв’язку задач є наступний:

1) проводять ряд допоміжних площин, які перетинають задану поверхню і площину;

2) будують лінії перетину допоміжних площин з заданою поверхнею і площиною;

Дата добавления: 2014-12-16