Лінійчасті поверхні

Криві поверхні в нарисній геометрії розглядають як сукупність послідовних положень лінії K (рис.7.7а), яка рухається за визначеним законом; при цьому, лінію K називають твірною. Частіш за все твірна K рухається, весь час перетинаючи деяку другу пряму N, що називається напрямною. Твірну і напрямну завжди можна поміняти місцями.

Залежно від твірної і напрямної кривої, а також від закону переміщення, поверхні можуть бути зведені в ряд класифікаційних груп. При цьому одна і та ж поверхня в ряді випадків може належати до декількох класифікаційних груп.

Класифікація, яку наведено нижче, не є вичерпною, однак дозволить скласти загальну уяву про систематизацію кривих поверхонь.

Залежно від вигляду твірної, поверхні розділяють на: лінійчасті, у яких твірними є прямі (рис. 7.7б) і нелінійчасті – з криволінійними твірними (рис.7.7а).

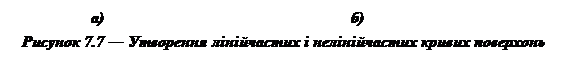До лінійчастих поверхонь належать ті поверхні у яких твірною є пряма лінія. Сюди, перш за все, належать прямий круговий циліндр і конус.

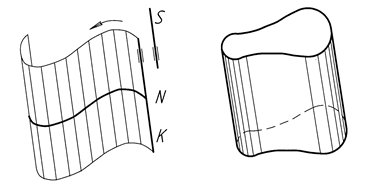Циліндричною поверхнею називають поверхню, яка утворена рухом прямої лінії (твірної), що залишається паралельною наперед вибраній прямій. Напрямною може бути довільна крива. На рисунку 7.8а зображена циліндрична поверхня, яка утворена твірною прямою K та напрямною кривою N так, що твірна K весь час залишається паралельною прямій S. Тіло, що окреслене (обмежене) циліндричною поверхнею, називається циліндром (рис. 7.8б).

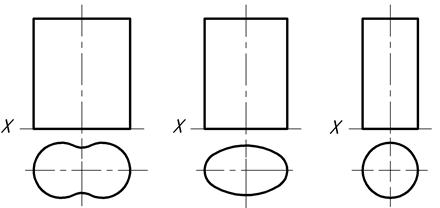
Циліндри розрізняють за видом кривої лінії, яку отримують в перерізі поверхні з площиною, що є перпендикулярною до твірної циліндра. Таку криву називають нормальним перерізом і назву циліндра визначає назва цієї кривої: циліндр загального вигляду (рис. 7.9а), еліптичний циліндр (рис. 7.9б), коловий циліндр (рис. 7.9в).

Коловий циліндр є поверхнею другого порядку.

Конічною поверхнею називають поверхню, яка утворена рухом прямої лінії K (твірної), що проходить через нерухому точку S і перетинає напрямлену криву, що може бути довільною кривою.

Тіло, яке обмежене конічною поверхнею, називають конусом. Точка S - вершина конуса (рис.7.10).

Якщо напрямною конуса є центральна крива, то пряма, що проходить через центр цієї кривої та вершину конуса і перпендикулярна площині напрямної кривої є віссю конуса.

Перетин конуса площиною, перпендикулярною до його осі, називають нормальним перерізом.

Коловий конус є поверхнею другого порядку. Якщо основа конуса є нормальним перерізом, то конус буде називатися прямим (рис. 7.11а,б): похилий конус зображений на рисунку 7.11в.

При обертанні твірної кожна її точка здійснює рух по колу, площина якого розміщена перпендикулярно до осі обертання. Ці кола називають паралелями. Площина, яка проходить через вісь поверхні обертання, називається меридіальною площиною, а лінія її перетину з поверхнею обертання називається меридіаном.

До лінійчастих поверхонь відносяться поверхні, всі твірні яких паралельні до постійної напрямної площини, яка називається площиною паралелізму.

До них відносяться:

Циліндроїди – поверхні, які утворені рухом прямої лінії, що у всіх своїх положеннях, паралельна до деякої заданої площини (площини паралелізму) і перетинає дві різні криволінійні напрямні різних виглядів.

Коноїди – окремий випадок циліндроїда, який є лінійчастою поверхнею, що має площину паралелізму і дві напрямних, але одну пряму, другу криву.

Якщо поверхня коноїда утворена прямою, яка ковзає одним кінцем по прямій, перпендикулярній до неї, а другим – по гвинтовій лінії і паралельно площині паралелізму, то його називають гвинтовим коноїдом (рис. 7.17).

До лінійчастих поверхонь відносяться такі поверхні, як: гіперболічні параболоїди, торси, евольвентні геліксоїди і т.д. Вивчення будови і властивостей цих поверхонь розглянуті у спеціальних курсах нарисної геометрії.

Дата добавления: 2014-12-16