При перетині лінійчастих поверхонь з площиною вигідно знаходити точки перетину твірних поверхні (прямих) із заданою площиною

В перетині знайдених ліній відмічають точки шуканої лінії перетину.

Задача 5 Задано прямий, коловий, горизонтально-проектуючий циліндр, який стоїть своєю основою на p₁ і перетинається січною площиною Σ. Знайти три проекції та дійсну величину перерізу (рис.3.16).

Для побудови проекцій перерізу, поверхню циліндра ділимо на однакову кількість рівних частин – на рис.3.16поділ зроблено на 8 частин. На горизонтальній проекції показано точки 1₁,2₁…,8₁. На фронтальній проекції проведено твірні, які перетинаються із січною площиною Σ в точках 1₂, 2₂….,8₂. Фронтальна проекція перерізу виродиться у відрізок 1₂7₂, який збігається з фронтальним слідом Σ₂ січної площини, а горизонтальна проекція перерізу збігається з горизонтальною проекцією циліндра. Профільна проекція в перерізі буде плавною кривою – еліпсом, велика вісь якого дорівнює відрізку 1₃5₃, а мала вісь – відрізку 3₃7₃. Проміжними точками еліпса є точки, отримані перетином відповідних твірних циліндра (2,4,6,8) з площиною S. При побудові, коли січна площина проходить під кутом 45˚ до площини проекцій p₁, профільна проекція виродиться в коло, діаметр якого дорівнює діаметру основи циліндра. Дійсна величина еліпса може бути побудована, наприклад, одним із способів перетворення епюра (розділ 2). У даному випадку використаємо спосіб суміщення, що є найраціональніший для даної задачі.

	Рисунок 3.16

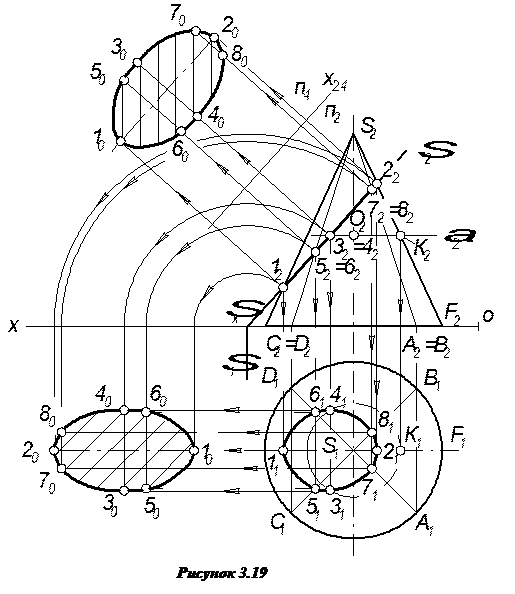
Задача 6 Побудувати проекції та дійсну величину перерізу прямого кругового конуса фронтально-проекційною площиною S (рис.3.17, 3.18, 3.19).

Розв’язок показано поетапно на рисунках 3.17, 3.18, 3.19. У даному випадку січна площина перерізає конус по еліпсу, який співпадає із фронтальним слідом S₂ січної площини у пряму 1₂2₂, що буде великою віссю еліпса. Горизонтальна проекція осі визначається за точками 1₁2₁ (рис.3.18,а).

Рисунок 3.17

Для знаходження малої осі еліпса ділимо фронтальну проекцію осі навпіл і через середину її проводимо горизонтальну площину a. Фронтальна проекція малої осі вироджується в точку 3₂=4₂, а горизонтальна проекція буде відрізком 3₁4₁ (рис.3.18,б) _. Величина цього відрізка визначається у точках перетину кола, побудованого радіусом О₂К₂, з центру S₁, від перерізу конуса допоміжною площиною a, з напрямком малої осі. Проміжними точками еліпса є точки, отримані перетином відповідних твірних конуса (SC, SD, SA, SB) із площиною S (рис.3.18,в та 3.18,г).

Дійсну величину фігури перерізу визначаємо способом суміщення площини S ₃ з горизонтальною площиною p₁, або ж заміною площин проекцій, які описані у розділі 2.

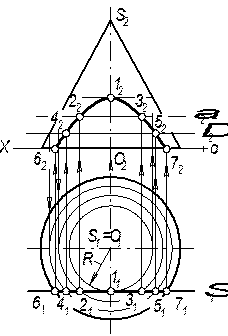
Задача 7 Побудувати проекції та дійсну величину перерізу прямого кругового конуса фронтально-проекційною площиною t (рис.3.20).

На рис.3.20 конус перетинається фронтально-проекційною площиною, яка паралельна твірній конуса. Лінією перетину буде парабола, для побудови якої проводимо допоміжні горизонтальні площини (a, D, j), які перетинають конус по колах, а площину t — по її горизонталях. На перетині цих ліній лежать шукані точки параболи.

Фронтальна проекція перерізу співпадає з фронтальним слідом площини t, а на горизонтальній площині p₁ проектується у вигляді параболи. Дійсна величина параболи знайдена шляхом суміщення площини t з площиною проекцій p₁ (розділ 2).

	Рисунок 3.20

Задача 8 Побудувати переріз конуса фронтальною площиною S (рис.3.21).

Перерізом конуса буде гіпербола, оскільки січна площина паралельна p₂, але не проходить через вісь конуса, тому гіпербола спроектується на площину p₁ у вигляді прямої, яка збігатиметься із слідом S₁, а на площину p₂ — у дійсну величину. Характерні точки гіперболи 6 і 7, в яких вона перетинає площину p₁ і коло основи конуса зі слідом S _1.

Рисунок 3.21

Ще одна характерна точка гіперболи — вершина 1. Горизонтальна проекція 1₁ знаходиться на середині відрізка 6₁7₁. Для побудови фронтальної проекції 1₂ проводимо з точки S₁ коло радіусом R=S₁1₁. Щоб знайти фронтальну проекцію цього кола, проводимо лінію зв’язку до перетину з крайньою твірною конуса. Знаходимо місце знаходження цього кола на фронтальній площині і точки 1₂ на ньому. Допоміжні точки гіперболи 2, 3, 4, 5 можна знайти за допомогою допоміжних січних площин a і D, яка аналогічна побудові точки 1.

ЗАПИТАННЯ ТА ЗАВДАННЯ ДЛЯ САМОПЕРЕВІРКИ

1 У чому полягає загальний спосіб побудови перерізу поверхні площиною?

2 Що називається перерізом поверхні?

3 Які лінії отримують при перерізі многогранників та кривих поверхонь площиною?

4 Які лінії називають лініями зрізу?

5 Суть способу побудови точок перетину прямої з поверхнею.

6 Які допоміжні площини застосовують для знаходження точок перетину прямої з поверхнею?

7 Що називається розгорткою поверхні?

8 Що являє собою розгортка многогранника?

9 Способи побудови розгортки призми.

10 Яким способом будується розгортка піраміди?

11 Якими способами виконуються розгортки циліндрів, конусів?

12 Яка з ліній на поверхні обертання є екватором (горлом, головним меридіаном)?

	а) h
б) q
в) k
г) l
д) f

13 Яка з ліній на поверхні кулі є екватором (головним меридіаном) кулі?

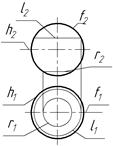
	а) f1,f2
б) r2,r1
в) h1,h2
г) l2,l1

14 фронтальну проекцію точки А побудовано вірно?

	а) A2
б) А2^1
в) А2^2

15 Яка точка є горизонтальною проекцією точки C?

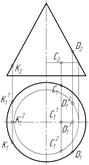
	а) C1^1
б) C1^2
в) C1

16 Яка з точок не належить поверхні конуса?

	а) A
б) B
в) C
г) D

17 По якій кривій в просторі площина перетинає кулю (сферичну поверхню)?

а) еліпс; б) коло; в) гіпербола; г) парабола.

18 Яка з ліній на поверхні кулі є лінією зміни видимості на фронтальній (горизонтальній) площині проекцій?

а) будь яка параллель; б) екватор; в) головний меридіан.

19 Проекції якої точки на поверхні кулі знайдені вірно?

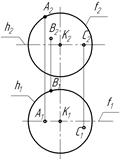
	а) С
б) К
в) B
г) A

20 Які з точок, проекції яких задані на кресленні, є точками зміни видимості на

горизонтальній площині проекцій?

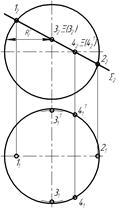
	а) 1 і 2
б) 3 і 3^1
в) 4 і 4^1

21 Яку форму має горизонтальна проекція лінії перерізу кулі площиною D, S, L?

	а) коло радіуса R3
б) коло радіуса R2
в) еліпс з осями (3,4) і (1,2)
г) еліпс з осями (7,8) і (5,6)

22 Яка форма горизонтальної проекції лінії перерізу кулі площиною S?

	а) еліпс з осями (3,4) і (1,2)
б) кола радіуса (0131)
в) еліпс з осями (3141) і (5161)
г)кола радіуса (0232)

23 Контур якого перерізу сфери площинами D, S, L, Т спроєціюється в дійсну величину на фронтальну площину проекцій?

	а) S
б) D
в) Т
г) L

24 Назвіть геометричну форму фігури перерізу циліндра площиною D (S)?

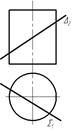
	а) коло
б) еліпс
в) чотирикутник
г) парабола

25 З яких ліній в просторі складається контур лінії перерізу циліндра площинами S і D?

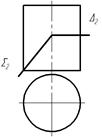
	а) відрізок і частина кола
б) з частини кола і частини еліпса
в) з частин двох еліпсів
г) відрізок і парабола

26 Який переріз циліндра відповідає положенню січної площини D (S, L)?

	а) рис.1
б) рис.2
в) рис.3
г) рис.4

27 Яку форму перерізу бічної поверхні конуса отримаємо при перетині його площиною, яка паралельна одній твірній конуса?

а) парабола; б) коло; в) еліпс; г) трикутник; д) гіпербола.

28 Яку форму перерізу бічної поверхні конуса отримаємо при перетині його площиною, яка перетинає всі твірні конуса, але не перпендикулярна до його осі?

а) парабола; б) коло; в) еліпс; г) трикутник; д) гіпербола.

29 Коло якого радіуса потрібно провести, щоб побудувати горизонтальні проекції точок К і N?

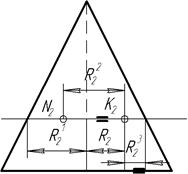
	а)
б)
в)
д)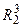
Фронтальна проекція конуса

30 Яка з точок на поверхні конуса є горизонтальною проекцією точки М?

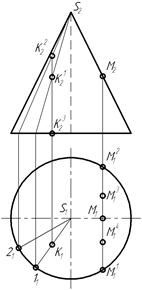
	а)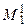
б)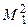
в)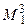
г)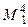
д)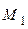

31 Назвати номери точок, проекції яких при побудові параболи можна визначити без проміжних побудов?

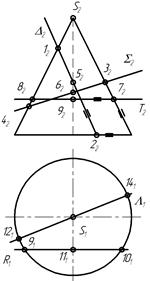
	а) 4 і 3
б) 7 і 8
в) 12 і 14
г) 1 і 2
д) 9 і 10

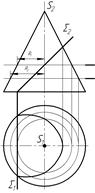
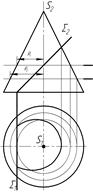
32 На якому рисунку контур перерізу конуса площиною S побудовано вірно?

а) рис. 1	б) рис. 2	в) рис. 3

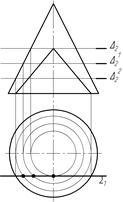
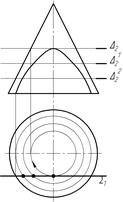
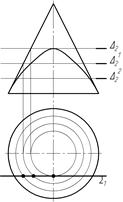
33 На якому рисунку вірно побудована лінія перетину конуса площиною S?

а) рис. 1	б) рис. 2	в) рис. 3

34 Яка точка є найвищою точкою лінії перерізу конуса площиною S?

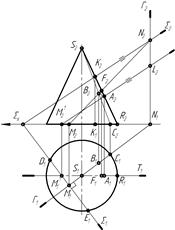
	а) К (К1К2)
б) F (F1F2)
в) A (A1A2)
г) B (B1B2)

35 Частини яких кривих ліній складають контур перерізу бічної поверхні конуса площинами D, S, R?

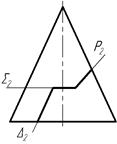
	а) еліпс, парабола, гіпербола
б) парабола, коло, еліпс
в) парабола, прямокутник, еліпс
г) гіпербола, еліпс, трикутник

Дата добавления: 2014-12-16