Гранні поверхні

ПОВЕРХНІ ТА ЇХ ВЗАЄМНИЙ ПЕРЕТИН

РОЗДІЛ 3

Поверхня – одне з основних геометричних понять. В алгебраїчній та аналітичній геометрії поверхня задається як геометричне місце точок, координати яких задовольняють певне алгебраїчне рівняння. Розглядаючи процес задання і зображення поверхонь на кресленні вважається, що будь-яка поверхня, як частина двовимірного простору, може бути утворена в результаті руху в просторі однієї лінії по іншій. Лінія, яка під час руху утворює дану поверхню, називається твірною, а лінія, по якій рухається твірна — напрямною. Твірна може змінювати положення, зберігаючи свою форму, або змінювати і положення і форму. Твірні і напрямні можуть бути як прямими, так і кривими, що приводить до утворення великої кількості різноманітних поверхонь.

Багатогранником називають частину простору, який обмежено з усіх боків плоскими багатокутниками, у яких кожна сторона одного з них є одночасно стороною другого. Ці багатокутники називаються гранями, сторони їх – ребрами, а вершини їх — вершинами багатогранника.

Зображення багатогранника зводиться до зображення його ребер, тобто ліній перетину граней і вершин — точок перетину ребер (рис. 3.1).

Рисунок 3.1

Сукупність усіх ребер і вершин багатогранника є його сіткою. Найпростішим багатогранником є тетраедр, який має чотири грані. Тетраедр задають проекціями його чотирьох вершин і шести ребер, що сполучають вершини (рис. 3.1). Одночасно визначається видимість ребер за допомогою конкуруючих точок.

Побудова точки та прямої на поверхні багатогранника виконується аналогічно побудові точок і прямих у площині, оскільки кожна грань багатогранника є частиною площини (рис. 3.2).

На рис. 3.2 точка К (К₂;К₁) належить основі АВС призми АВСDEF, оскільки К₂ – фронтальна проекція точкилежить на фронтальній проекції А₂В₂С₂ основи призми. Точка L належить поверхні призми, а саме, бічній грані призми АСDE, оскільки лежить на прямій ЕТ, яка належить цій грані і проходить через дві точки цієї грані Е і Т. Точка Т лежить на СD, точка Е лежить на АЕ.

На рисунку 3.3 точка К належить грані SAB піраміди SABС, оскільки лежить на прямій SТ, яка в свою чергу належить цій грані, бо має з нею дві спільні точки S і Т.

Відрізок ЕF належить грані SBС, бо точки Е і F лежать на сторонах SB і SС цієї грані.

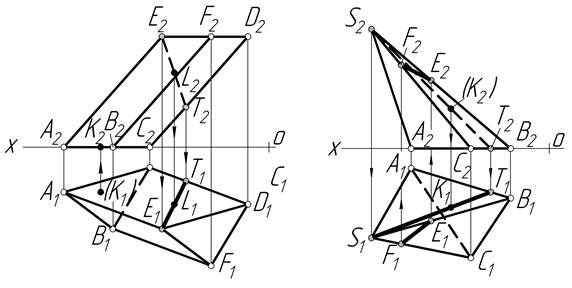
Рисунок 3.2 Рисунок 3.3

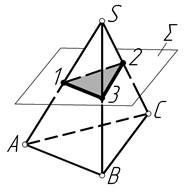
Лінії перетину багатогранника площиною визначаються по точках перетину ребер багатогранника з площиною, або по лініях перетину граней багатогранника з даною площиною. Перший шлях розв’язку називають методом ребер, другий — методом граней (рис. 3.4).

	Метод ребер 1®SA´S 2®SC´S 3®SB´S		Метод граней   12®SAC´S 23®SBC´S 13®SAB´S

Рисунок 3.4

У першому випадку задача зводиться до визначення точки перетину прямої з площиною, у другому – до визначення лінії перетину площин. Якому із способів віддати перевагу, необхідно вирішувати у кожному конкретному випадку. Фігуру, отриману від перетину багатогранника площиною, називають багатокутником (фігурою) перерізу. Число сторін багатокутника перерізу дорівнює числу граней, які перетинаються січною площиною.

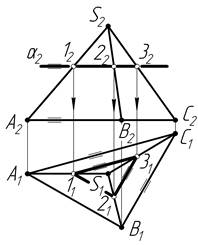
Фігура перерізу проектується на площину проекцій без спотворення (у справжню, дійсну величину), якщо січна площина паралельна площині проекцій. На рисунку 6.10 тригранна піраміда SABC перерізана горизонтальною площиною a (a₂). Ця площина перетнула піраміду по трикутнику 123. Горизонтальна проекція фігури перерізу 1₁2₁3₁ є дійсною величиною фігури перерізу. Фронтальна проекція 1₂2₂3₂ виродилася в лінію, яка співпала з фронтальним слідом площини a₂.

	Рисунок 3.5

При перетині поверхні багатогранника проекційною площиною задача зводиться, як правило, до визначення точок перетину відрізків прямих (ребер багатогранників) з проекційною площиною. Залежно від положення проекційної площини одна з проекцій багатогранника перерізу вироджується у відрізок прямої.

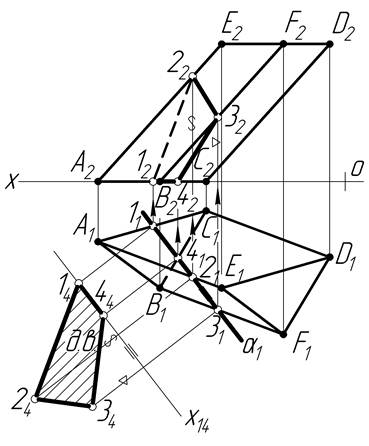
Задача 1 Побудувати дійсну величину перерізу похилої призми горизонтально-проекційною площиною a (рис.3.6).

При перетині багатогранника горизонтально-проекційною площиною у відрізок прямої вироджується горизонтальна проекція фігури перерізу. На рисунку 3.6 похилу призму перетнуто горизонтально-проекційною площиною a (a₁). Тому горизонтальна проекція перерізу виродиться у відрізок 1₁3₁, який співпадає з a₁. Точки 4₁ і 2₁ також лежать на цьому відрізку і співпадають з a₁ (точки перетину горизонтального сліду площини із ребрами призми).

А₁С₁ ´ a₁ = 1₁

В₁С₁ ´ a₁ = 4₁

А₁Е₁ ´ a₁ = 2₁

В₁F₁ ´ a₁ = 3₁

Фронтальні проекції точок 1, 2, 3, 4 знаходимо з умови належності їх відповідним ребрам призми. Точки 1, 4 лежать на основі трикутника АВС, тому по лінії проекційного зв’язку знаходимо фронтальні їх проекції 1₂, 4₂ на А₂В₂С₂. Точка 2 належить ребру АЕ, тому по лінії проекційного зв’язку піднімаємо її на А₂Е₂. Так само точка 3 належить ребру ВF і по лінії проекційного зв’язку піднімаємо її на В₂F₂. З’єднавши точки 1₂, 2₂, 3₂, 4₂ з урахуванням видимості, одержимо фронтальну проекцію перерізу. Для знаходження дійсної величини перерізу використаємо спосіб заміни площин проекцій. Нову вісь Х₁₄ проведемо паралельно сліду a₁ на будь-якій відстані і спроектуємо переріз у нову площину проекцій p₁₄. Дійсна величина перерізу ─ 1₄2₄3₄4₄.

	Рисунок 3.6

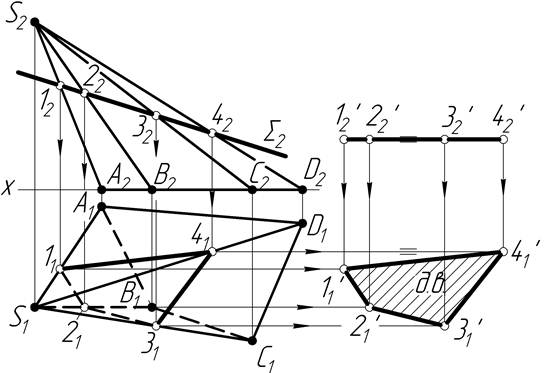
Задача 2 Побудувати дійсну величину перерізу похилої піраміди фронтально-проекційною площиною S (рис.3.7).

При перетині багатогранника фронтально-проекційною площиною у відрізок прямої вироджується фронтальна проекція фігури перерізу. На рис. 3.7 похилу піраміду перерізано фронтально-проекційною площиною S (S₂). Тому фронтальна проекція перерізу виродиться у відрізок 1₂4₂, який співпадає з S₂. Точки 2₂ і 3₂ також лежать на цьому відрізку і співпадають з S₂ (точки перетину фронтального сліду площини із ребрами піраміди).

S₂A₂´S₂=1₂

S₂B₂´S₂=2₂

S₂C₂´S₂=3₂

S₂D₂´S₂=4₂

Горизонтальні проекції точок 1, 2, 3, 4 знаходимо з умови належності їх відповідним ребрам піраміди SABCD. Точка 1 лежить на ребрі SA, точка 2 на ребрі SB і т.д., тому знаходимо їх горизонтальні проекції на відповідних горизонтальних проекціях ребер S₁A₁; S₁B₁ і т.д. Далі, з’єднавши точки 1₁, 2₁, 3₁, 4₁ з урахуванням видимості, одержимо горизонтальну проекцію перерізу. Для знаходження дійсної величини перерізу використаємо спосіб плоско-паралельного переміщення. Для цього фронтальну проекцію перерізу 1₂2₂3₂4₂ розташуємо у горизонтальне положення 1₂′2₂′3₂′4₂′. Кожна точка, згідно цього способу, переміщається в площині, паралельній до p₂ (показано стрілками). Отже горизонтальна проекція 1₁′2₁′3₁′4₁′ і є дійсною величиною перерізу.

	Рисунок 3.7

Задача 3 Побудувати розгортку нижньої частини призми, зрізаної фронтально-проекційною площиною S (рис.3.8).

На основі теоретичного матеріалу, описаного в попередньому підрозділі, знайдемо проекції перерізу прямої призми фронтально-проекційною площиною S, а також побудуємо дійсну величину фігури перерізу способом суміщення, сумістивши площину S з горизонтальною площиною проекцій.

Побудувати розгортку бічної поверхні прямої призми неважко, бо її горизонтально-проекційні ребра проектуються на площину проекцій p₂ у дійсну величину, а сторони нижньої основи зображаються на p₁ також без спотворення довжини. Для того, щоб розгорнути призму, треба вибрати ребро, по якому уявно розріжемо призму для побудови розгортки бічної поверхні.

Як правило, вибирають те ребро, на якому знаходиться найнижча точка перерізу, або ж ребро, яке не зрізане. У даному випадку вибрано ребро АА′. Побудову розгортки починаємо з розгортки бокової поверхні. Для цього на горизонтальній прямій відкладаємо від обраної точки А₀′ три відрізки, кожний з яких дорівнює довжині ребра основи призми. Через позначені точки проводимо вертикальні прямі і послідовно переносимо на них з вертикальної площини проекцій довжини бічних ребер нижньої зрізаної частини призми. Точки 1₀, 2₀, 3₀ сполучаємо ламаною лінією. Побудувавши розгортку бічної поверхні призми, до однієї з її ребер приєднуємо дійсну величину фігури перерізу і нижню основу. Побудову виконуємо методом засічок. Одержане зображення – повна розгортка нижньої зрізаної частини призми. Лінії зрізу і контур розгортки наводимо суцільною основною товстою лінією, а лінії згину – штрихпунктирною з двома крапками.

Рисунок 3.8

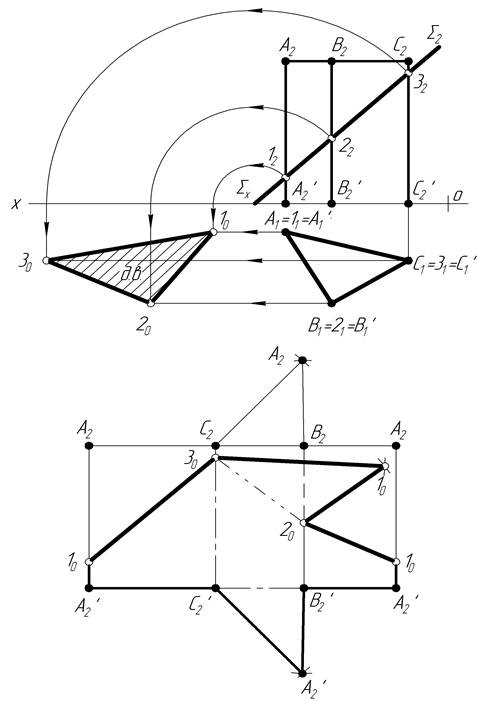
Задача 4 Побудувати розгортку нижньої частини піраміди, зрізаної фронтально-проекційною площиною S (рис.3.9).

На основі теоретичного матеріалу, описаного у попнрндньому підрозділі, знаходимо проекції перерізу прямої піраміди фронтально-проекційною площиною S. Слід зауважити, що для знаходження точки 2₁ на профільному ребрі SB використаємо допоміжну горизонтальну площину α, проведену через точку 2₂. Площина α перетинає піраміду по трикутнику, подібному до трикутника основи піраміди. Вершина трикутника 2 і буде шуканою точкою. Побудову дійсної величини фігури перерізу знайдемо способом суміщення, сумістивши площину S з горизонтальною площиною проекцій.

Розгортка бічної поверхні піраміди являє собою плоску фігуру, яка складається з трикутників – бічних граней піраміди. Щоб отримати повну розгортку піраміди, необхідно до розгортки бічної поверхні добудувати дійсну величину многокутника основи. При побудові розгортки треба мати дійсну величину бокових ребер SA, SB, SC. Для цього ребро SC повернемо навколо осі, яка проходить через точку S перпендикулярно до площини проекцій p₁, до положення, паралельного до площини проекцій p₂ – S₁C₁′. На фронтальній проекції нове положення S₂C₂′ – це дійсна величина ребра SC. На цьому ребрі SC₂′ – визначимо дійсну величину зрізаних ребер піраміди. Для цього з точок 1₂, 2₂, 3₂ проводимо горизонтальні лінії, які на відрізку SC₂ відтинають S1₀, S2₀, S3₀, що є дійсними величинами зрізаних ребер піраміди.

Таким чином, всі необхідні елементи для побудови розгортки піраміди знайдено.

Спочатку будуємо розгортку бічної поверхні піраміди. Вона являє собою плоску фігуру, складену в певному порядку з трьох трикутників – дійсних величин бічних граней: S₀А₀ = S₀В₀ = S₀С₀ = S₂C₂′.

Попередньо виберемо ребро SА (на якому знаходиться точка 1 – найнижча точка перерізу), по якому уявно розріжемо бокову поверхню піраміди. Виберемо довільну точку S₀ на чистому полі місця креслення і методом засічок будуємо бокову розгортку піраміди. На кожному з ребер S₀А₀, S₀В₀, S₀С₀ відкладаємо точки 1₀, 2₀, 3₀, S₂1₀ = S₀1₀ на ребрі SА, S₂2₀ = S₀2₀ на ребрі SВ, S₂3₀ = S₀3₀ на ребрі SС. Сполучимо точки А₀, 1₀, 3₀, 2₀, 1₀, А₀, В₀, С₀ прямими лініями, отримаємо розгортку зрізаної бічної поверхні піраміди.

Приєднавши до неї дійсні величини фігур основи і перерізу, побудованих методом засічок, дістанемо розгортку зрізаної (нижньої) частини поверхні піраміди.

Дата добавления: 2014-12-16