
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Операции над векторами в координатной форме
|
|
|
|
Прямоугольная декартова система координат Oxy на плоскости задается совокупностью точки О (начало системы координат) и пары перпендикулярных единичных векторов  ,
,  При этом ось Ox, направление которой совпадает с направлением вектора
При этом ось Ox, направление которой совпадает с направлением вектора 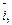 называется осью абсцисс. Oсь y, совпадающая по направлению с вектором
называется осью абсцисс. Oсь y, совпадающая по направлению с вектором 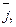 – осью ординат. Вся плоскость называется координатной плоскостью xOy. За масштабную единицу выбирают длину
– осью ординат. Вся плоскость называется координатной плоскостью xOy. За масштабную единицу выбирают длину 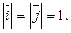
Координатами точки М являются соответственно алгебраические проекции точки М на координатные оси Ox и Oy. Таким образом, точке М на плоскости соответствует упорядоченная пара (x, y) действительных чисел x и y. Пишут: M (x, y).
Каждой точке М на плоскости соответствует единственный радиус-вектор  который имеет те же координаты, что и точка М. Пишут:
который имеет те же координаты, что и точка М. Пишут:  Вектор
Вектор  может быть представлен также в виде линейной комбинации векторов
может быть представлен также в виде линейной комбинации векторов 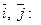
 .
.
Если на плоскости заданы точки A (x 1, y 1), B (x 2, y 2), то
 ,
,
длина
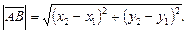 (5)
(5)
Пусть  тогда единичный вектор (орт) есть
тогда единичный вектор (орт) есть
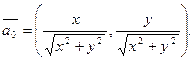 (6)
(6)
При этом координаты орта  задают направление вектора
задают направление вектора 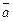 и называются направляющими косинусами. Если
и называются направляющими косинусами. Если  то
то
 . (7)
. (7)
Если  , то верны формулы
, то верны формулы
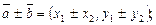 (8)
(8)
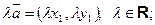 (9)
(9)
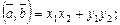 (10)
(10)
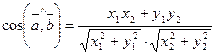 . (11)
. (11)
Для коллинеарных векторов 
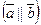 выполняется
выполняется
 .
.
Координаты точки C (xc, yc), делящей отрезок AB в отношении λ > 0, находят по формулам
 (12)
(12)
Пример 1. Вектор 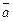 образует с вектором
образует с вектором  угол
угол 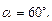 Найти координаты вектора
Найти координаты вектора 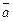 на плоскости, если
на плоскости, если 
Решение. Орт  вектора
вектора 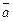 на плоскости xOy имеет координаты
на плоскости xOy имеет координаты 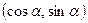 . Используя формулы (6) и (7), получаем
. Используя формулы (6) и (7), получаем  Так как
Так как  то
то  .
.
Пример 2. Найти координаты векторов, определяемых диагоналями параллелограмма, построенного на векторах 
Решение. Известно, что сумма и разность векторов 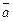 и
и 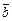 определяют диагонали параллелограмма, построенного на них. Значит,
определяют диагонали параллелограмма, построенного на них. Значит, 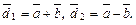 Тогда
Тогда

и, значит,
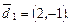
Аналогично
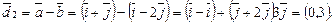
Пример 3. Координаты левого конца отрезка AB и его середины M соответственно равны A (–1, –5) и M (3, –2). Найти координаты точки В.
Решение. Пусть В (xB, yB). Середина отрезка делит его длину в отношении 1:1, т. е. λ = 1. Значит, из формул (12) имеем 
откуда получаем
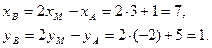
Приходим к ответу: В (7, 1).
Пример 4. Даны векторы  Вычислить:
Вычислить:
1) 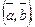 2)
2)  3)
3)  4)
4) 
Решение. 1. Используя формулу (10), имеем

2. Согласно формулам (8), (9), получаем

Тогда, на основании формулы (10) вычисляем

Получить тот же результат можно и несколько по-другому. Используем свойства скалярного произведения, а затем формулы (5) и (10):
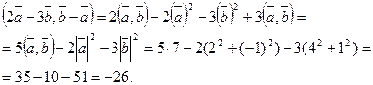
3. Найдем координаты вектора  , используя формулы (8) и (9)
, используя формулы (8) и (9)
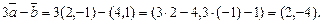
Значит, по формуле длины вектора (5) получаем
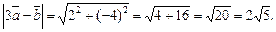
В качестве второго способа решения примера можно использовать следующий. Поскольку 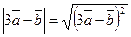 , то
, то
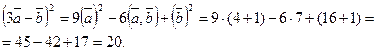
Находим
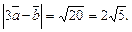
4. Используем формулу (11) и получаем

Пример 5. Даны векторы  Найти косинус угла между векторами
Найти косинус угла между векторами  и
и 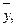 для которых
для которых 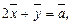

Решение. Выразим  из первого заданного соотношения:
из первого заданного соотношения: 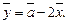 Тогда, подставив во второе соотношение, получим
Тогда, подставив во второе соотношение, получим 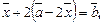 откуда
откуда

Значит, на основании формулы (11), получаем

Пример 6. Пусть векторы  получены из векторов
получены из векторов 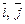 поворотом относительно точки О на угол
поворотом относительно точки О на угол  (рис. 8). Представить произвольный вектор
(рис. 8). Представить произвольный вектор  в виде линейной комбинации векторов
в виде линейной комбинации векторов 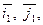 если
если 
 |
Рис. 8
Решение. Зафиксируем прямоугольную систему координат  с единичными векторами
с единичными векторами 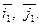 В этой системе координат определим направляющие косинусы векторов
В этой системе координат определим направляющие косинусы векторов
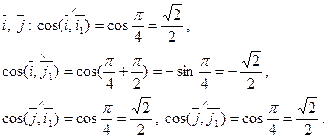
Это значит, что

откуда
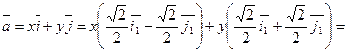
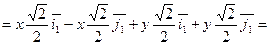

Задания для самостоятельного решения
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 1223; Нарушение авторских прав?; Мы поможем в написании вашей работы!