Гипербола

Гиперболой называется геометрическое место точек плоскости, координаты которых удовлетворяют уравнению

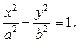(25)

где .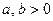

Параметры гиперболы:

Точки F ₁(–c, 0), F ₂(c, 0), где 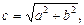называются фокусами гиперболы, при этом величина 2 с (с > a > 0) определяет междуфокусное расстояние. Точки А ₁(– а, 0), А ₂(а, 0) называются вершинами гиперболы, при этом А ₁ А ₂ = 2 а образует действительную ось гиперболы, а В ₁ В ₂ = 2 b – мнимую ось (В ₁(0, – b), B ₂(0, b)), О – центр гиперболы.

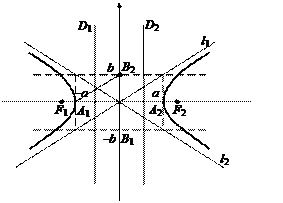Рис. 19

Величина 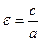называется эксцентриситетом гиперболы, она характеризует меру «сжатости» гиперболы;

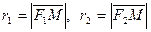– фокальные радиусы гиперболы (точка М принадлежит гиперболе), причем r ₁ = a + εx, r ₂ = – a + εx для точек правой ветви гиперболы, r ₁ = – (a + εx), r ₂ = – (– a + εx) – для точек левой ветви;

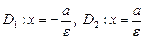– директрисы гиперболы;

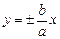– уравнения асимптот.

Для гиперболы справедливо: ε > 1, директрисы не пересекают границу и внутреннюю область гиперболы, а также обладают свойством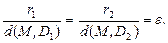

Говорят, что уравнение

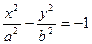(26)

задает уравнение гиперболы, сопряженной данной (рис. 20). Его можно записать также в виде

.

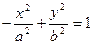В таком случае ось 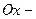мнимая, фокусы лежат на оси 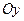. Все остальные параметры определяются аналогично как для гиперболы (25).

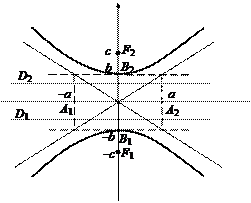Рис. 20

Точки гиперболы обладают важным характеристическим свойством: абсолютное значение разности расстояний от каждой из них до фокусов есть величина постоянная, равная 2 a (рис. 19).

Для параметрического задания гиперболы в качестве параметра t может быть взята величина угла между радиус-вектором точки, лежащей на гиперболе, и положительным направлением оси Ox:

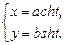
Пример 1. Привести уравнение гиперболы

9 x ² – 16 y ² = 144

к каноническому виду, найти еепараметры, изобразить гиперболу.

Решение. Разделим левую и правую части заданного уравнения на 144: 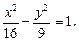Из последнего уравнения непосредственно следует: a = 4, b = 3, c = 5, O (0, 0) – центр гиперболы. Фокусы находятся в точках F ₁(–5, 0) и F ₂(5, 0), эксцентриситет ε = 5/4, директрисы D ₁ и D ₂ описываются уравнениями D ₁: x = –16/5, D ₂: x = 16/5, асимптоты l ₁ и l ₂ имеют уравнения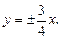

Сделаем чертеж. Для этого по осям Ox и Oy симметрично относительно точки (0, 0) отложим отрезки А ₁ А ₂ = 2 а = 8 и В ₁ В ₂ = 2 b = 6 соответственно. Через полученные точки А ₁(–4, 0), А ₂(4, 0), В ₁(0, –3), В ₂(0, 3) проведем прямые, параллельные координатным осям. В результате получим прямоугольник (рис. 21), диагонали которого лежат на асимптотах гиперболы. Строим гиперболу

Рис. 21

Для нахождения угла φ между асимптотами гиперболы воспользуемся формулой

.

,

откуда получаем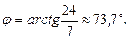

Пример 2. Определить тип, параметры и расположение на плоскости кривой, уравнение которой

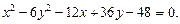
Решение. С помощью метода выделения полных квадратов упростим правую часть данного уравнения:

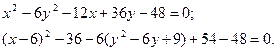
Получаем уравнение

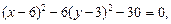
которое делением на 30 приводится к виду

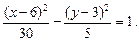
Это уравнение гиперболы, центр которой лежит в точке 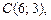действительная полуось – 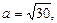мнимая полуось – 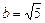(рис. 22).

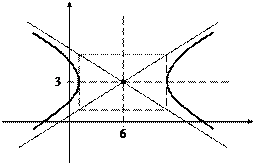Рис. 22

Пример 3. Составить уравнение гиперболы, сопряженной относительно гиперболы 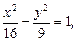определить ее параметры и сделать чертеж.

Решение. Уравнение гиперболы, сопряженной данной, –

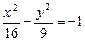или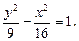

Действительная полуось b = 3, мнимая – а = 4, половина междуфокусного расстояния 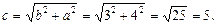Вершинами гиперболы служат точки B ₁(0, –3) и В ₂(0, 3); ее фокусы находятся в точках F ₁(0, –5) и F ₂(0, 5); эксцентриситет ε = с / b = 5/3; директрисы D ₁ и D ₂ задаются уравнениями D ₁: y = –9/5, D ₂: y = 9/5; уравнения 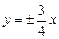являются уравнениями асимптот (рис. 23).

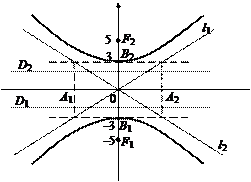Рис. 23

Заметим, что для сопряженных гипербол общими элементами являются вспомогательный «прямоугольник» и асимптоты.

Пример 4. Написать уравнение гиперболы с полуосями a и b (a > 0, b > 0), если известно, что ее главные оси параллельны координатным осям. Определить основные параметры гиперболы.

Решение. Искомое уравнение можно рассматривать как уравнение гиперболы 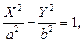которое получается в результате параллельного переноса старой системы координат на вектор 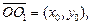где (x ₀, y ₀) – центр гиперболы в «старой» системе координат. Тогда, используя соотношения между координатами произвольной точки М плоскости в заданной и преобразованной системах

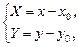
получим уравнение гиперболы

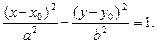
Определим параметры. Центр гиперболы определяет точка O ¢(x ₀; y ₀), а значит, действительная ось задается уравнением x = x ₀,а мнимая – уравнением y = y ₀. Ее вершинами являются точки 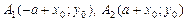, а асимптотами являются прямые 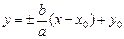. Половина междуфокусного расстояния 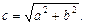Тогда фокусы гиперболы находятся в точках 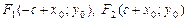, эксцентриситет

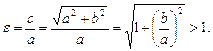
Директрисы D ₁ и D ₂ задаются уравнениями

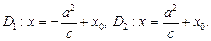
Пример 5. Написать уравнение гиперболы, имеющей вершины в фокусах эллипса 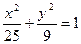, а фокусы – в вершинах этого эллипса.

Решение. Уравнение 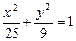означает, что фокусами эллипса являются точки 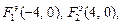а вершины, лежащие на главной оси, находятся в точках 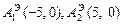(так как ).

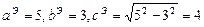Тогда для искомой гиперболы известно, что

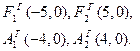
Значит, основные параметры гиперболы есть:

.

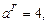
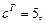
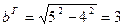Используя данную информацию, приходим к уравнению гиперболы

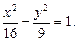
Задания для самостоятельного решения

Дата добавления: 2014-12-16