Парабола

III уровень

3.1. Гипербола касается прямых 5 x – 6 y – 16 = 0, 13 x – 10 y – – 48 = 0. Запишите уравнение гиперболы при условии, что ее оси совпадают с осями координат.

3.2. Составьте уравнения касательных к гиперболе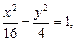

1) проходящих через точку A (4, 1), B (5, 2) и C (5, 6);

2) параллельных прямой 10 x – 3 y + 9 = 0;

3) перпендикулярных прямой 10 x – 3 y + 9 = 0.

Параболой называется геометрическое место точек плоскости, координаты которых удовлетворяют уравнению

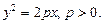
Параметры параболы:

Точка F (p /2, 0) называется фокусом параболы, величина p – параметром, точка О (0, 0) – вершиной. При этом прямая OF, относительно которой парабола симметрична, задает ось этой кривой.

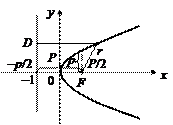Рис. 24

Величина 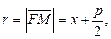где M (x, y) – произвольная точка параболы, называется фокальным радиусом, прямая D: x = – p /2 – директрисой (она не пересекает внутреннюю область параболы). Величина 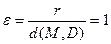называется эксцентриситетом параболы.

Основное характеристическое свойство параболы: все точки параболы равноудалены от директрисы и фокуса (рис. 24).

Существуют иные формы канонического уравнения параболы, которые определяют другие направления ее ветвей в системе координат (рис. 25).:

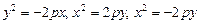
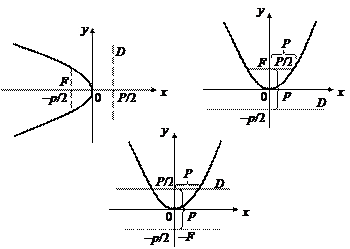Рис. 25

Для параметрического задания параболы в качестве параметра t может быть взята величина ординаты точки параболы:

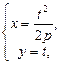
где t – произвольное действительное число.

Пример 1. Определить параметры и форму параболы по ее каноническому уравнению:

1) 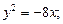2)

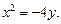
Решение. 1. Уравнение y ² = –8 x определяет параболу с вершиной в точке О (0; 0), симметричную относительно оси Оx. Ее ветви направлены влево. Сравнивая данное уравнение с уравнением y ²= –2 px, находим: 2 p = 8, p = 4, p /2 = 2. Следовательно, фокус находится в точке F (–2; 0), уравнение директрисы D: x = 2 (рис. 26).

Рис. 26

2. Уравнение x ² = –4 y задает параболу с вершиной в точке O (0; 0), симметричную относительно оси Oy. Ее ветви направлены вниз. Сравнивая данное уравнение с уравнением x ² = –2 py, находим: 2 p = 4, p = 2, p /2 = 1. Следовательно, фокус находится в точке F (0; –1), уравнение директрисы D: y = 1 (рис. 27).

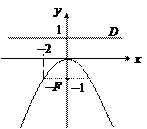
Рис. 27

Пример 2. Определить параметры и вид кривой x ² + 8 x – 16 y – 32 = 0. Сделать чертеж.

Решение. Преобразуем левую часть уравнения, используя метод выделения полного квадрата:

x ² + 8 x – 16 y – 32 =0;

(x + 4)² – 16 – 16 y – 32 =0;

(x + 4)² – 16 y – 48 =0;

(x + 4)² – 16(y + 3).

В результате получим

(x + 4)² = 16(y + 3).

Это каноническое уравнение параболы с вершиной в точке (–4; –3), параметром p = 8, ветвями, направленными вверх (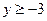), осью x = –4. Фокус находится в точке F (–4; –3 + p /2), т. е. F (–4; 1) Директриса D задается уравнением y = –3 – p /2 или y = –7 (рис. 28).

Рис. 28

Пример 3. Написать уравнение кривой, все точки которой равноудалены от прямой y = 3 и точки F (0; 3).

Решение. Точка F (0; 3) лежит на оси Oy и находится с прямой y = –3 по разные стороны от начала координат, причем на одинаковом расстоянии (d = 3). Это позволяет заключить, что искомой кривой является парабола x ² = 2 py с параметром p = 2 · 3 = 6, т. е. x ² = 12 y (рис. 29).

Рис. 29

Пример 4. Составить уравнение параболы с вершиной в точке V (3; –2) и фокусом в точке F (1; –2).

Решение. Вершина и фокус данной параболы лежат на прямой, параллельной оси Ox (одинаковые ординаты), ветви параболы направлены влево (абсцисса фокуса меньше абсциссы вершины), расстояние от фокуса до вершины равно p /2 = 3 – 1 = 2, p = 4. Значит, искомое уравнение

(y + 2)² = –2 · 4(x – 3) или (y + 2)² = = –8(x – 3).

Задания для самостоятельного решения

I уровень

1.1. Определите параметры параболы и построить ее:

1) y ² = 2 x; 2) y ² = –3 x;

3) x ² = 6 y; 4) x ² = – y.

1.2. Напишите уравнение параболы с вершиной в начале координат, если известно, что:

1) парабола расположена в левой полуплоскости симметрично относительно оси Ox и p = 4;

2) парабола расположена симметрично относительно оси Oy и проходит через точку M (4; –2).

3) директриса задана уравнением 3 y + 4 = 0.

1.3. Составьте уравнение кривой, все точки которой равноудалены от точки (2; 0) и прямой x = –2.

II уровень

2.1. Определить тип и параметры кривой:

1) x ² – 8 x + 2 y + 18 = 0; 2) x = 2 y ² – 12 y + 14.

Сделать чертеж.

2.2. Составьте уравнение параболы с вершиной в начале координат, фокус которой находится в точке пересечения прямой 3 x – 2 y + 5 = 0 с осью ординат.

2.3. Составьте уравнение параболы с вершиной в точке V (3, –2) и фокусом F (3; 0).

2.4. Составьте уравнение параболы с вершиной в точке (–1; 1) и уравнением директрисы y – 1 = 0.

2.5. Составьте уравнение параболы с фокусом и директрисой .

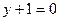III уровень

3.1. Составьте уравнение параболы, проходящей через точки (–1; 1), (1; 3) и (31, 9).

3.2. Найдите расстояние от левого фокуса эллипса до прямой, проходящей через точки его пересечения с параболой y ² = 12 x.

3.3. Составьте полярное уравнение параболы, приняв ее вершину за полюс, а ее ось – за полярную ось.

3.4. Докажите, что множество точек, равноудаленных от точки 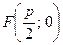и прямой 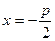, есть парабола .

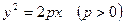3.5. Составьте параметрические уравнения параболы 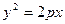, принимая в качестве параметра ординату .

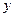3.6. Определите уравнение кривой в прямоугольных координатах и постройте ее, если она задана параметрически с помощью уравнений .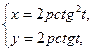

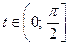Дата добавления: 2014-12-16