Вопрос№15Понятия и виды детерминированных факторных моделей, цели и способы их преобразования

Цель: изучить понятие и виды детерминированных факторных моделей; рассмотреть цели и способы преобразования факторных моделей.

Модели факторных систем строятся от общего к частному, приближаясь к простым, т. е. элементным, неделимым факторам.

Факторную систему можно изобразить математически или схематически. С помощью структурно-логических моделей можно определить наличие связи между результативными и факторными показателями, а также установить направление этих связей. Математическая модель – это буквенное изображение факторной системы. В ней взаимосвязь между результативными и факторными показателями отражена математическим уравнением.

Различают исходные и развитые факторные модели.

Исходная модель – это модель, в которой показано влияние на результат факторов первого порядка.

Например, объем произведенной продукции за год – это произведение среднегодовой численности рабочих и годовой выработки одного рабочего (формула 3.1), т. е. используется модель вида y = a × b.

Развитая модель охватывает большое число факторов. Она может быть получена путем детализации одного или нескольких факторов первого порядка, которые разделяются на факторы второго и последующего порядков (формула 3.2), где фактор первого порядка – годовая выработка – разделяется на два фактора второго порядка: дневную выработку и среднее число отработанных одним рабочим дней, а дневная выработка разделяется в свою очередь на два фактора третьего порядка: часовую выработку рабочего и среднюю продолжительность рабочего дня одного рабочего в часах.

В детерминированном анализе выделяют четыре основных типа факторных моделей:

· аддитивные;

· мультипликативные;

· кратные;

· комбинированные (смешанные).

Аддитивные модели – это модели, в которых результативный показатель (Y) представлен как сумма факторов (х_і):

(3.3)

Мультипликативные модели – это модели, в которых результативный показатель (Y) можно представлять как произведение факторов (х_і):

(3.4)

Кратные модели – это модели, где результат (Y) представлен частным от деления одного фактора на другой:

(3.5)

Смешанные модели – это модели, в которых сочетаются в различных комбинациях предыдущие типы моделей, например:

(3.6)

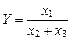и т. п. (3.7)

Такие модели при проведении экономического анализа встречаются часто.

Любой тип моделей можно преобразовать в зависимости от целей анализа.

Преобразование аддитивных факторных моделей осуществляется за счет расчленения одного из факторных показателей на его составные элементы. Так, при условии, что а = d – e, модель (3.8) преобразуется в модель (3.9):

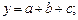(3.8)

(3.9)

Например, прибыль предприятия (П) включает прибыль от реализации продукции (П_РП), прибыль от операционной деятельности (П_ОП) и прибыль от внереализационной деятельности (П_ВН):

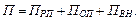(3.10)

Это исходная аддитивная модель, в которой представлены факторы первого порядка. Расчленим первый фактор – прибыль от реализации на составляющие, представив ее как разницу между объемом реализованной продукции (РП) и себестоимостью реализованной продукции (С_РП):

(3.11)

В результате исходная модель преобразуется в развитую и будет выглядеть следующим образом:

(3.12)

В данной модели объем реализованной продукции и себестоимость реализованной продукции являются факторами второго порядка, а прибыль от операционной деятельности и прибыль от внереализационной деятельности – факторами первого порядка.

Расчленение факторов можно продолжить и представить объем реализованной продукции в следующем виде:

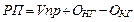, (3.13)

где О_НГ – остатки нереализованной продукции на начало года;

О_КГ – остатки нереализованной продукции на конец года.

Себестоимость реализованной продукции в свою очередь представлена в виде следующей формулы:

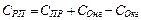, (3.14)

где С_ПР – себестоимость произведенной продукции;

С_Онг – себестоимость остатков нереализованной продукции на начало года;

С_Окг – себестоимость остатков нереализованной продукции на конец года.

Тогда исходная модель будет выглядеть следующим образом:

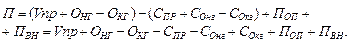(3.15)

Данная модель представлена факторами первого и третьего порядка.

Преобразование мультипликативных факторных моделей осуществляется путем последовательного расчленения факторов исходной модели на факторы-сомножители. Если исходная модель имеет вид:

(3.16)

то при a = c × d, b = e × f, получается следующая модель:

(3.17)

Для преобразования кратных моделей используются следующие способы:

· удлинение;

· формальное разложение;

· расширение;

· сокращение.

Способ удлинения предусматривает удлинение числителя исходной модели (х ₁) путем его замены на алгебраическую сумму показателей. Если исходная кратная модель имеет вид:

, (3.18)

то при x ₁ = a + b + с, она преобразуется в смешанную (комбинированную) модель:

(3.19)

В качестве примера рассматривается кратная модель показателя «затраты на один рубль произведенной продукции» (З), определяемого отношением себестоимости произведенной продукции (Спр) к объему произведенной продукции (Vпр):

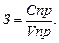(3.20)

Если показатель себестоимости разложить на элементы затрат – материальные затраты (МЗ), затраты на оплату труда (ЗП), амортизацию (А), прочие затраты (ПЗ), то модель преобразуется следующим образом:

(3.21)

где МЕ – материалоемкость;

ЗПЕ – зарплатоемкость;

АЕ – амортизациоемкость;

ПЗЕ – прочие затраты на один рубль произведенной продукции.

Таким образом, кратная модель преобразуется в аддитивную с новым набором факторов, которые оказывают влияние на величину затрат на один рубль произведенной продукции.

Способ формального разложения предусматривает удлинение знаменателя исходной модели. Если исходной моделью является отношение (3.18), то при x ₂ = a + b + c + d, модель может иметь следующий вид:

. (3.22)

Способ формального разложения на практике встречается часто. Например, рентабельность произведенной продукции (Р_ПР) рассчитывается как отношение прибыли от производства (П_ПР) к себестоимости произведенной продукции (С_ПР):

. (3.23)

В данном случае показатель принимается в виде коэффициента (без умножения на 100%). Так как С_ПР = МЗ + ЗП + А + ПЗ, то исходная модель (3.23) преобразуется в следующую модель:

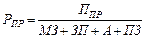. (3.24)

Таким образом, исходная кратная модель преобразована в смешанную (комбинированную), которая более широко характеризует зависимость результативного показателя (Р_ПР) от влияния нового набора факторов.

Способ расширения предусматривает расширение исходной модели путем умножения числителя и знаменателя исходной кратной модели на один или несколько новых одинаковых показателей и выражается следующим образом:

. (3.25)

Конечная формула может быть представлена в виде:

, (3.26)

где n -количество факторов в модели.

Таким образом, исходная кратная модель преобразована в мультипликативную модель с новым набором факторов.

Этот способ широко применяется при анализе, например, среднегодовой выработки одного рабочего (Вргод), которая определяется как отношение объема произведенной продукции к среднесписочной численности рабочих:

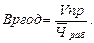(3.27)

Если числитель и знаменатель этого отношения умножить на количество дней, отработанных всеми рабочими, т. е. человекодни (Кд), то результат не изменится, но в итоге перегруппировки формула будет выглядеть следующим образом:

, (3.28)

где Врдн – дневная выработка одного рабочего, полученная как отношение объема произведенной продукции к числу дней, отработанных всеми рабочими;

Д – число дней, отработанных одним рабочим.

Способ сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя на один и тот же показатель. Исходная модель преобразуется в модель вида:

. (3.29)

В данном случае получена модель того же типа (кратная), но с другим набором факторов.

Данный способ можно использовать, например, при анализе фондоотдачи (ФО), которая определяется отношением объема произведенной продукции к среднегодовой стоимости основных производственных фондов () и выражается формулой

. (3.30)

Если и числитель и знаменатель разделить на численность рабочих, то в числителе получают годовую выработку одного рабочего (Вргод), а в знаменателе – фондовооруженность труда рабочих (ФВ):

. (3.31)

В результате вышеприведенных преобразований получены совершенно другие наборы факторных показателей, влияющих на результативный показатель. Для преобразования одной и той же модели могут последовательно применяться несколько различных способов.

Дата добавления: 2014-12-16