Расчеты стержней на прочность и жесткость

Для обеспечения нормальной работоспособности детали необходимо, чтобы фактически существующие напряжения растяжения (сжатия) не превышало допускаемого.

Напряжение в расчетном сечении растянутого (сжатого) стержня может быть определено из уравнения (2.5) [КА].

Для оценки прочности стержня необходимо сопоставить действующее напряжение с допускаемым согласно условию прочности:

(2.13)

С помощью условия (2.13) могут быть решены задачи следующих трех типов:

1 Расчет на прочность существующей конструкции с определенными размерами. При этом определяют напряжение в деталях конструкции и величину их сравнивают с допустимым напряжением. Такой расчет носит название проверочного.

2 Определение предельной (допускаемой) нагрузки для детали с определенными разрезами поперечного сечения 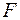и допускаемым напряжением 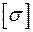. Здесь из соотношения (2.13) получим . Это вариант проверочного расчета.

3 Определение площади поперечного сечения стержня по заданной продольной силе и допускаемому напряжению:

(2.14)

Такие расчеты называют расчетами на прочность. Если при этом определяют вполне конкретные параметры сечения, т.е. основные размеры его, например, ширина, высота при прямоуголном сечении, диаметр – при цилиндрической форме сечения, то расчет называют проектировочным.

В некоторых случаях работоспособность конструкции определяют не величиной предельной нагрузки или предельного напряжения, а величиной предельной деформации . В этом случае из уравнения (2.7) находят фактическую деформацию и сопоставляют ее с предельной, т.е.

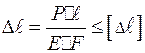(2.15)

Неравенство (2.15) называют условием жесткости, а расчеты, проводимые по этому неравенству, называют расчетами на жесткость.

Как известно, системы (конструкции) подвергающиеся расчету, разделяют на статически определимые и статически неопределимые.

Для решения статически неопределимых задач, кроме уравнений статики абсолютно твердого тела, необходимо использовать уравнения упругих деформаций.

Общий метод решения статически неопределимых задач сводится к следующему.

1 Составляя уравнение статики и сопоставляя количество этих уравнений с числом неизвестных, устанавливают степень статической неопределимости системы.

2 Отбросив лишние связи, заменяют их лишними неизвестными, тем самым превращая рассматриваемую систему в статически определимую, именуемую основной системой.

3 Для определения лишних неизвестных составляют условие деформации системы, смысл которого заключается в том, что основная система под действием приложенной нагрузки и лишних неизвестных деформируется так же, как и заданная статически неопределимая система.

4 Условия деформации системы находят в виде уравнений деформации. При этом число уравнений деформации должно соответствовать числу лишних неизвестных.

5 После определения лишних неизвестных из уравнений статики определяют остальные неизвестные.

Ниже приведены два примера расчетов систем

Дата добавления: 2014-12-16