Расчеты на прочность и жесткость. При изгибе балки под действием внешних моментов в ее поперечных сечениях возникают внутренние изгибающие моменты Ми

При изгибе балки под действием внешних моментов в ее поперечных сечениях возникают внутренние изгибающие моменты М_и. то же самое имеет место при изгибе балки поперечной силой, но здесь наряду с М_и возникает дополнительно поперечная сила Q.

Рассмотрим методику определения М_и и Q на примере балки, изображенной на рисунке 3.4.

Рисунок 3.4 Схема нагружения балки поперечными силами и изгибающими моментами.

Пусть балка, лежащая на опорах А и В нагружена вертикальными силами P₁; P₂ распределенной нагрузкой интенсивности q и моментами М₁ и М₂, действующими в вертикальной плоскости симметрично балки. Опорные реакции R_А и R_В определяют из уравнений равновесия.

Рассмотрим поперечное сечение балки mn, определяемое абсциссой х. Указанное сечение делит внешние силы и моменты, приложенные к балке, на две взаимоуравновешивающиеся системы, из которых одна действует слева, другая – справа от данного сечения.

Каждую из этих систем можно привести к центру тяжести С рассматриваемого сечения.

Поперечная сила Q в любом поперечном сечении балки численно определяется как алгебраическая сумма сил, расположенных по одну сторону от сечения. Для сечения mn (рисунок 3.4) в соответствии с установленным правилом знаков («+» - по часовой стрелке, «-» - против) имеем:

, (3.1)

или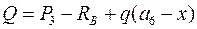

Главный момент внешних, действующих на балку на одну сторону от сечения mn, называют – изгибающим моментом в данном сечении. Этот момент (обозначим его М_и ) будем рассматривать как алгебраическую величину, имеющую положительное значение, если он действует так, что ось балки изгибается выпуклостью вниз (рисунок 3.5, в) и отрицательное в противоположном случае (рисунок 3.5, г).

Рисунок 3.5 Действие поперечной силы и изгибающего момента М.

Изгибающий момент М_и в любом сечении балки численно определяется как алгебраическая сумма моментов, действующих на балку внешних сил, расположенных по одну сторону от рассматриваемого сечения, относительно центра тяжести этого сечения.

При этом для левой части балки моменты сил считаются положительными, если они направлены по отношению к центру тяжести сечения по левой стороне, и отрицательными, если против часовой стрелки, для правой части – наоборот.

Таким образом, для сечения mn (рисунок 3.4) имеем:

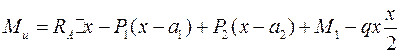
или (3.2)

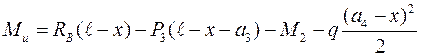
Поперечная сила Q и изгибающий момент М_и в общем случае зависит от положения сечения, т.е. от абсциссы х. найдем зависимость между Q и М_и, а также Q и q. Для этого определим поперечную силу Q и изгибающий момент М_и в сечении , смещенном относительно сечения mn на бесконечно малое расстояние 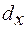(рисунок 3.4):

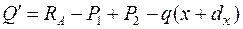(3.3)

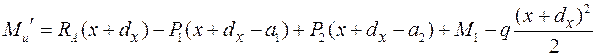(3.4)

Определим изменения dM изгибающего момента и dQ – поперечной силы при переходе от сечения mn к сечению 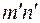. Вычитая соответственно (3.2) из (3.4) и (3.1)из (3.3), имеем:

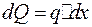; , откуда, учитывая выражение (3.1), получаем:

или 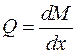, (3.5)

т.е. поперечная сила в данном сечении равна первой производной от изгибающего момента по абсциссе сечения (теорема Муравского Д.И.). Аналогично получим:

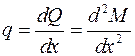, (3.6)

т.е. вторая производная от изгибающего момента по абсциссе сечения равна интенсивности распределенной нагрузки.

Полученные зависимости используют при построении эпюр (характера изменения) изгибающих моментов и поперечных сил (графики зависимости М_и и Q от координаты х сечения – есть эпюра). Эпюры дают наглядное представление изменения М_и и Q по длине балки и позволяют устанавливать место нахождения опасных сечений.

Рассмотрим методику построения этих эпюр для простейших случаев нагружения.

Дата добавления: 2014-12-16