Примеры расчетов

Случай 1 Консольная балка нагружена сосредоточенной силой Р на конце консоли (рисунок 3.6 а).

В месте зацепления А балки возникает реактивный момент M_R и опорная реакция R_A.

Рисунок 3.6 Схема и эпюра нагружения консольной балки под действием концевой сосредоточенной силы.

Составим уравнение равновесия сил, действующих на балку:

;

.

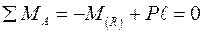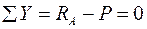Отсюда:

;

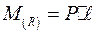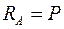
Определим изгибающий момент в сечении и эпюры расположенном на расстоянии Х от опоры А. силы, действующие слева от рассматриваемого сечения, создают момент:

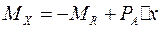
После подстановки значений реактивного момента и опорной реакции приходим к следующему уравнению:

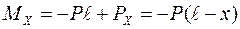
При х = 0 и х = 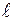получаем изгибающий момент соответственно у эпюры А и на конце балки:

;

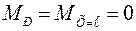
Построим эпюру изгибающих моментов. Для этого выбираем нулевую линию, параллельную оси балки.

Откладывая в некотором масштабе М_м от этой линий вниз (М_Х<0) под соответствующими сечениями балки найденные значения М_Х получаем искомую эпюру (рисунок 3.6, б). Так как зависимость М_Х от координаты сечения в данном случае является линейной, то эпюра изгибающих моментов представляет собой наклонную прямую. Абсолютная величина изгибающего момента достигает наибольшего значения у закрепленного конца балки.

Рассмотренную задачу можно решить проще, если за начало отсчета координаты сечения принять точку преломления силы Р и определять главный момент сил, находящихся справа от сечения. Обозначив новую координату через Х₁, имеем 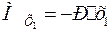, а на концах балки получаем:

;

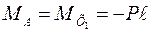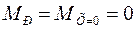
Для определения поперечных сил обратимся к теореме Журавского:

,

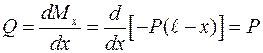Т.е. поперечная сила 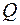постоянна по всей длине балки. Эпюра поперечных сил в данном случае представляет собой прямую, параллельную нулевой линии и отстоящую от нее на расстоянии З (рисунок 3.6,в) в масштабе M_Q.

Случай 2 Консольная балка нагружена по всей длине равномерно распределенной нагрузкой с интенсивностью q (рисунок 3.7,а).

Рисунок 3.7 Схема и эпюра нагружения консольной балки с равномерно распределенной нагрузкой.

Реактивный момент в этом случае 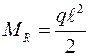, опорная реакция 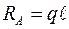. Заменив равномерно распределенную нагрузку, действующие на правую часть балки, сосредоточенной силой, равной qx, действующей на расстоянии 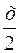от выбранного сечения, имеем:

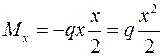
Определим значение изгибающих моментов для характерных точек:

Х = 0; М₀ = 0; 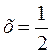; ; 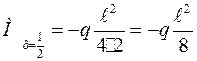х = ; .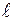

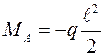Как видно из уравнения для М_Х, эпюра изгибающих моментов в данном случае представляет собой параболу второй степени, обращенную вогнутостью вниз, имеющую вершину в начале координат (рисунок 3.7,б). Эту параболу можно построить по точкам.

Абсолютная величина изгибающего момента имеет наибольшее значение 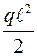у защемленного конца балки. На основании теоремы Журавского: 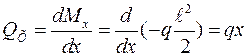; следовательно 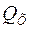= 0; .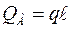

Из уравнения для 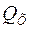следует, что эпюра поперечных сил представляет собой наклонную прямую (рисунок 3.7, в).

Случай 3 Балка на двух опорах нагружена сосредоточенной силой З (рисунок 3.8, а).

Рисунок 3.8 Схема и эпюра нагружения двух опорной балки сосредоточенной силой.

Уравнение равновесия балки:

; .

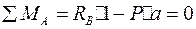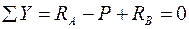Отсюда: , .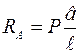

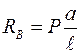Рассмотрим два сечения, определяемых координатами Х₁ и Х₂. первое сечение расположено между опорой А и точкой приложения силы З, второе – между опорой В и точкой приложения силы Р.

Изгибающий момент в сечении I–I, если рассматривать левую часть балки, будет:

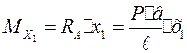
Изгибающий момент в сечении II–II будет:

,

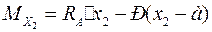Т.е. изгибающий момент на двух участках балки определяется двумя линейными уравнениями и, следовательно, эпюра изгибающих моментов состоит из двух отрезков наклонной прямой (рисунок 3.8,б).

Величина изгибающих моментов в характерных точках:

; ;

; ;

; .

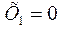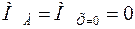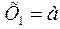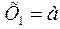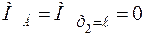Если сила Р приложено в середине пролета, т.е. а=в= 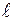/2, то 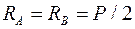, а максимальный изгибающий момент в этом случае: .

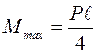Так как изгибающий момент характеризует двумя линейными функциями, то из теоремы Журавского следует, что на каждом из двух участков между опорами и точкой приложения сосредоточенной силы З поперечная сила остается постоянной.

Действительно, для участка АС:

;

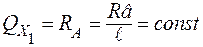для участка СВ:

.

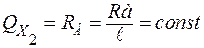Таким образом, эпюра поперечных сил представляет собой два прямолинейных отрезка, параллельных нулевой линии (рисунок 3.8, в). В точке приложения нагрузки Р поперечная сила при этом меняет скачкообразно знак.

Случай 4 Балка на двух опорах нагружена равномерно распределенной нагрузкой интенсивность q (рисунок 3.9, а).

Рисунок 3.9 Схема и эпюра нагружения двух опорной балки равномерно распределенной нагрузкой.

Равнодействующая равномерно распределенной нагрузки равна q 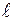и приложена в середине пролета балки, поэтому: .

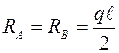Изгибающий момент в сечении I–I на расстоянии Х от левой опоры: .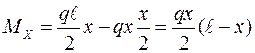

Изгибающий момент в характерных точках:

; ; .

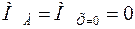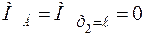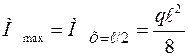Следовательно, эпюра изгибающих моментов представляет собой параболу второй степени (рисунок 3.9, б).

Величину поперченной силы в сечении I–I определяют как сумму внешних сил, действующих слева от сечения:

,

т.е. поперечная сила изменяется по линейному закону. Определим ее величину в характерных точках:

; ; .

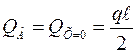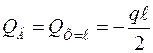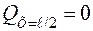Таким образом, эпюра поперечных сил представляет собой наклонную прямую, пересекающую нулевую линию в середине пролета балки (рисунок 3.9, в).

Случай 5 Балка на двух опорах нагружена в сечении С сосредоточенным моментом М (рисунок 3.10, а).

Рисунок 3.10 Балки на двух опорах нагружена в сечении С сосредоточенным моментом М.

В данном случае имеем: .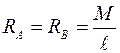

Изгибающие моменты для сечений I–I и II–II, отстоящих соответственно на расстоянии Х₁ и Х₂ от опор А и В, равны: 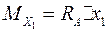; 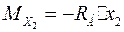, т.е. на участках АС и СВ изгибающий момент выражается линейными функциями координаты сечения.

В характерных точках имеем: , .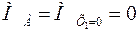

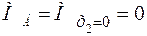Для сечения С получаем два результатов (рисунок 3.10, б): , ,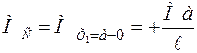

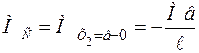Т.е. в сечении С изгибающий момент изменяется скачкообразно.

Эпюра изгибающих моментов представлена двумя прямолинейными отрезками, образующими с нулевой линей одинаковый угол (рисунок 3.10, б).

Поперечная сила по всей длине балки одинакова:

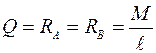
Эпюра поперечных сил – прямая, параллельная нулевой линии (рисунок 3.10,в).

Случай 6 Балка на двух опорах с равными по длине консолями, нагруженными на концах равными сосредоточенными силами Р (рисунок 3.11,а).

Рисунок 3.11 Балка на двух опорах с равными по длине консолями, нагруженными на концах равными сосредоточенными силами.

Причем: .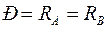

Так как при сосредоточенных силах (нагрузках) изгибающий момент на различных участках балки выражается в виде линейных функций от координаты сечения, то эпюра изгибающих моментов представлена отрезком прямой и для ее построения достаточно определить изгибающие моменты в характерных сечениях балки:

; ; ; .

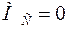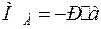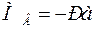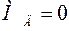При этом эпюра изгибающих моментов будет такой, как это показано на рисунке 3.11, б, т.е. в данном случае это равнобедренная трапеция.

Поперечные силы могут быть получены при помощи теоремы Журавского. При этом на консолях поперечные силы будут:

;

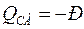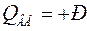
Так как изгибающий момент между опорами А и В сохраняет постоянное значение, то поперечная сила здесь 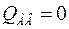, а эпюра будет такой, как она представлена на рисунке 3.11, в (случай чистого изгиба).

Случай 7 Балка на двух опорах, нагруженная двумя сосредоточенными силами, направленными в противоположные стороны (рисунок 3.12,а).

Рисунок 3.12

Опорные реакции:

; .

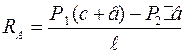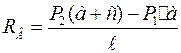В зависимости от величины сил 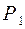и 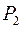, а также размеров а и в направление опорных реакций может отличаться от указанного на рисунке 3.12, а.

Изгибающие моменты в характерных сечениях балки, при указанном направлении опорных реакций:

; ; ; .

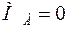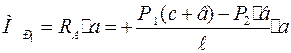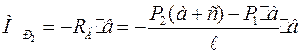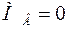Принимая во внимание линейную зависимость изгибающего момента от абсциссы сечения, строим эпюру изгибающих моментов. В выбранном масштабе М_м откладываем ординаты, соответствующие полученным в характерных сечениях значением изгибающего момента, и концы их соединяем отрезками прямой (рисунок 3.12, б).

Проектируя на вертикальную ось опорные реакции и заданные силы, получим поперечную силу для различных участков балки:

;

;

.

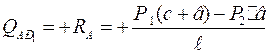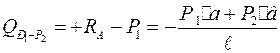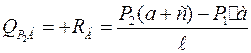Эпюра поперечных сил состоит из отрезков прямой, параллельной горизонтальной оси (рисунок 3.12, в).

Случай 8 Балка на двух опорах с консолью, нагруженной в концевом сечении с сосредоточенным моментом М (рисунок 3.13, а)

Рисунок 3.13

Опорные реакции М в данном случае равны по модулю, но направлены в противоположные стороны:

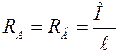
Изгибающий момент в характерных сечениях с учетом правил знаков:

; ; .

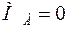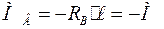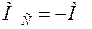Следовательно, на всем протяжении консоли изгибающий момент сохраняет постоянное значение, равное М. эпюра изгибающих моментов показана на рисунке 3.13,б. на протяжении пролета АВ поперечная сила: 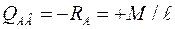(рисунок 3.13,в). На консоли: 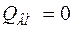, здесь имеет место чистый изгиб.

Дата добавления: 2014-12-16