Определение перемещений изгибаемой балки

Общая методика решения задач изгиба

Общая методика решения задач изгиба прямолинейного бруса сводится к следующему:

1 Составляют уравнения равновесия сил, действующих на балку

2 Определяют изгибающие моменты в характерных точках (сечениях).

3 Строят эпюру изгибающих моментов.

4 Определяют значения поперечных сил в характерных точках и строят эпюру поперечных сил.

5 Определение напряжения при изгибе:

где: - момент сопротивления сечения – чистое от деления момента инерции сечения 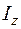относительно нейтральной оси на расстоянии от этой оси до наиболее удлиненной точки сечения:

6 Выполнение уравнения прочности:

7 Определение перемещений (прогиб и угол поворота балки) изгибаемой балки.

Ниже приведены два примера решения последней задачи.

Пример №1 Определить прогиб и угол поворота на свободном конце консоли (в точке 0) балки, изображенной на рисунке 3.6 (случай 2).

Решение Изгибающий момент в сечении на расстоянии х от правого конца:

Подставляя выражение изгибающего момента в дифференциальное уравнение упругой линии, получим:

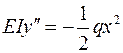
Интегрируя, имеем:

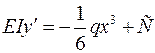(3.7)

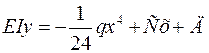(3.8)

Для определения постоянных С и Д используем граничные условия:

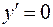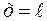при , отсюда ;

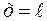при , отсюда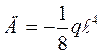

Таким образом уравнения (3.7) и (3.8) принимает вид:

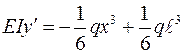(3.9)

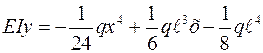(3.10)

Из этих уравнений (3.9) и (3.10) находим угол поворота и прогиб на свободном конце балки:

;

.

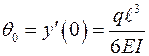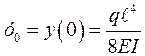Знак «–» в правой части последнего равенства указывает на то, что направление прогиба противоположно положительному направлению оси у.

Пример 2 Для балки, изображенной на рисунке 3.8 (случай 3) определить прогиб в точке приложения силы Р.

Решение Разбиваем балку не два участка и составляем дифференциальное уравнение упругой линии для каждого из них в отдельности, поскольку выражение изгибающего момента на этих участках различны. Сначала определяем опорные реакции:

; .

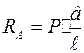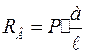Далее для первого участка имеем:

.

Поэтому дифференцированное уравнение упругой линии балки на этом участке принимает вид:

Интегрируя получаем:

(3.11)

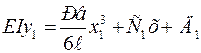(3.12)

Для второго участка имеем:

;

;

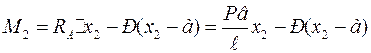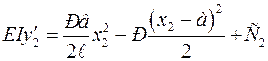(3.13)

(3.14)

Определим четыре постоянные интегрирования С₁; С₂; Д₁; Д₂.

Из условия непрерывности и гладкости упругой линии в точках соприкасаний рассматриваемых участков балки следует, что при 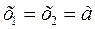соблюдаются условия: 1) 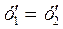откуда на основании (3.11) и (3.12) имеем 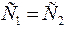; 2) откуда на основании уравнений (3.13) и (3.14) получим .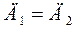

Из условий опирания концов балки найдем значения постоянных интегрирования. При 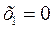прогиб . Пользуясь уравнением (3.12) получаем .

При прогиб 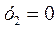из уравнения (2.13) находим:

Теперь определим неполную величину из уравнений (3.12) и (3.14), подставим в них найденные значения постоянных. Воспользуемся уравнением (3.12) учитывая, что при 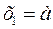, окончательно получим:

.

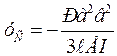Дата добавления: 2014-12-16