Расчеты на прочность и жесткость

Общие сведения

Кручение стержня круглого сечения

Цилиндрический брус, закрепленный одним концом и нагруженный парой сил с моментом М₁, действующим в плоскости поперечного сечения, подвергается деформации, называемой кручением. При этом крутящий момент М_К в любом сечении цилиндра, являющийся моментом внутренних сил упругости, численно равен моменту внешней пары сил, действующей на любую сторону от сечения, т.е.

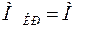(4.1)

Рассмотрение случая, когда на цилиндр действует несколько крутящих моментов разного направления (например, это ведущий вал редуктора с разновесной ступенью), показывает, что крутящий момент в любом сечении вала численно равен алгебраической сумме внешних моментов, действующих слева или справа от рассматриваемого сечения в плоскостях, перпендикулярных к оси вала т.е. .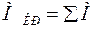

Рисунок 4.1 К установлению прочности и жесткости при кручении.

Рассмотрим элемент, выделенный сечениями I и II из цилиндра, конец которого закреплен неподвижно по указанной плоскости, а другой нагружен парой сил с моментом М (рисунок 4.1, а). В результате действия внешнего момента М возникает деформация кручения, при которой образующая цилиндра aвcd займет положение (рисунок 4.1, а).

Если сечение I–I, находящиеся на расстоянии х от нижнего конца цилиндра, повернулось на угол , то сечение II–II, находящиеся на расстоянии 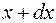от нижнего сечения, повернется на угол 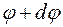(рисунок 4.1, б). Проведем из точки в прямую «вс» параллельно 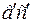. Тогда угол 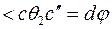. Элемент 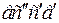до поворота сечения II относительно сечения I имел вертикальные боковые стороны, следовательно, абсолютный сдвиг элемента: .

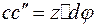Относительный сдвиг:

.

Обозначим 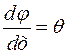, тогда 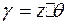, где 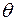– угол закручивания, отнесенный к единице длины цилиндра, называемой относительным углом закручивания.

Для цилиндров постоянного сечения, подвергаемых действию крутящего момента, 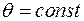. Так как в соответствии с принятыми допущениями радиусы при кручении остаются прямыми, то можно сказать, что для всякого элемента, лежащего внутри цилиндра на радиусе 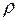, относительный сдвиг:

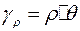(4.2)

По закону Гука напряжение в сечении цилиндра:

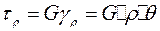(4.3)

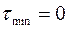при ;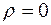

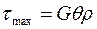
Из соотношения (4.3) следует, что напряжение внутри цилиндра изменяется по линейному закону пропорционально расстоянию от оси вращения. Минимальное напряжение, равное нулю, имеет место в центре поперечного сечения, а максимальное – на поверхности цилиндра (рисунок 4.1, в).

Элементарная касательная сила, перпендикулярная радиусу сечения, проведенному в центр тяжести элементарной площади dF, действующая на эту площадку с учетом соотношения (4.3), будет:

.

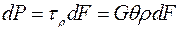Элементарный момент, создаваемый силой 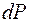относительно центра сечения:

.

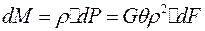Сумма таких элементарных моментов, взятая по всей площади поперечного сечения цилиндра, равна крутящему моменту 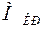, который действует в рассматриваемом сечении цилиндра и в данном конкретном случае равен внешнему моменту М:

.

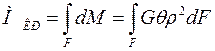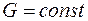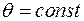Так как и , то .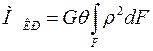

Но 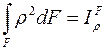– полярный момент инерции сечения. Поэтому:

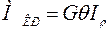(4.4)

Из соотношения (4.4) получим величину угла закручивания, отнесенного к единице длина цилиндра:

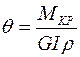(4.5)

Полный угол закручивания в радианах:

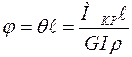(4.6)

или в градусах:

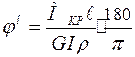(4.7)

Произведение модуля упругости второго рода на полярный момент инерции 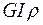называют жесткостью при кручении. Эта величина характеризует способность тела из данного материала с поперечным сечением длинного размера и форма сопротивляется деформации кручения. Таким образом, полный угол закручивания цилиндра прямо пропорционален крутящему моменту и длина цилиндра и обратно пропорционален жесткости при кручении.

Найдем зависимость напряжения от крутящего момента. В соответствии с (4.3) вместо 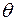подставляем его значение из (4.5):

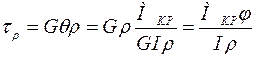
Отсюда (рисунок 4.1, в) наибольшее напряжение при кручении:

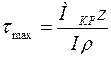(4.8)

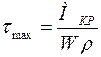или (4.9)

где 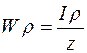– отношение полярного момента инерции к расстоянию от оси вращения до наиболее удаленной точки сечения; это отношение называют полярным моментом сопротивления.

Условие прочности при кручении будет выполнятся в том случае, если максимальное значение напряжения, возникающего при кручении, не превышает величины допускаемого напряжения, т.е. уравнение прочности при кручении имеет вид:

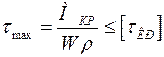(4.10)

Допускаемое напряжение при кручении для стали обычно принимают:

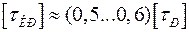
где 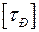– допускаемое напряжение при растяжении.

Приведем соотношение для определения полярного момента сопротивления:

для круга диаметром d с учетом выражения (4.4):

;

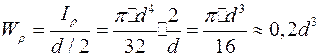для кольца, с учетом соотношения (4.5):

,

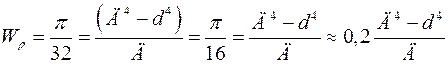где Д – наружный и 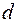внутренний диаметр кольца.

При 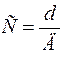полярный момент сопротивления кольца:

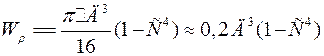
Ранее приведено уравнение прочности при проверочном расчете. Далее установим уравнение прочности при проектировочном расчете, когда необходимо определить параметры (в частности, диаметр 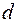вала) цилиндра при кручении.

Определить диаметр цилиндра 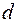, подвергнутого деформации кручения, можно исходя из двух посылок. В тех случаях, когда определяющей является прочность цилиндра, расчет ведут по соотношению (4.10). для сплошного цилиндра:

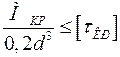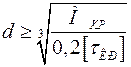; (4.11)

Когда определяющей является предельная деформация (угол закручивания), расчет ведут на жесткость. Из уравнения (4.7) имеем:

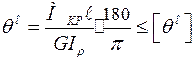(4.12)

где 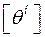– доп. угол закручивания на единицу длины, который в зависимости от назначения вала принимают в пределах 0,25 …1,0 град/м; 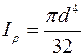– полярный момент инерции сплошного цилиндра.

Тогда диаметр вала сплошного сечения, на основании уравнения жесткости:

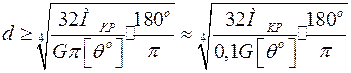(4.13)

Пользуясь уравнениями (4.10) и (4.12), можно решить и другую задачу: определить безопасную величину крутящего момента бруса, при котором обеспечивается необходимая прочность или жесткость.

Резюме по двум видам напряженного состояния – изгибу и кручению: основной параметр, влияющий на величину напряжения – момент, определяют с одной целью – выяснить выполняется ли условие прочности и допустимы ли линейные и угловые параметры деформации.

Дата добавления: 2014-12-16