Продольный изгиб (устойчивость сжатых стержней)

Форма равновесия в деформированном состоянии считается устойчивой, если система при любом малом отклонении от начального состояния равновесия возвращается к нему после снятия внешний нагрузки. В противном случае указанная форма равновесия является неустойчивой.

Переход системы из устойчивого состояния в неустойчивое называют потерей устойчивости, а границу этого перехода – критическим состоянием системы.

Если сжимающую нагрузку воспринимает короткий брус большого сечения (большой жесткости), рисунок 6.1, а, то на прочность и жесткость его рассчитывают по формулам для осевого сжатия (смотри пункт 2). В случае восприятия сжимающей нагрузки длинным стержнем (рисунок 6.1, б) последний может искривиться (рисунок 6.1, в), что не позволяет использовать здесь зависимости раздела 2.

Рисунок 6.1 Действие сжимающего усилия на стержень

Искривление стержня наступает в следствии того, что его ось практически всегда имеет небольшую начальную кривизну, а точка приложения силы несколько смещена от центра тяжести поперечного сечения стержня. При силе большей некоторой критической стержень будет работать уже не на чистое осевое сжатие, а сжатие и изгиб, что приводит к значительным прогибам и напряжениям. Стержень при этом либо разрушается, либо получит недопустимо большие деформации. Все это происходит при так называемых критических значениях воздействующей силы, которую рассматривают как опасную (предельно допустимую).

Под критической силой понимают такую силу, превышение которой вызывает потерю устойчивости первоначальной формы равновесия. При этом условие прочности можно записать так:

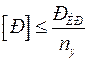(6.1)

где – допускаемая нагрузка;

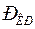– критическая сила;

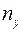– коэффициент запаса устойчивости.

Задача по определению величины критической силы сжатого стержня впервые была правильно решена Эйлером (середина 18 века):

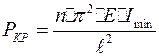(6.2)

где 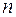– любое целое число (1,2,3,4 и т.д.);

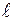– длина стержня.

Для практических расчетов используют зависимость:

(6.3)

называемую формулой Эйлера или для различных схем закрепления стержня:

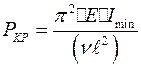(6.4)

где – приведенная длина стержня, а 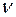– коэффициент приведения длины ( 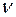=2,0…0,5).

Под действием загрузки 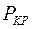в поперечных сечениях стержня возникают нормальные напряжения:

,

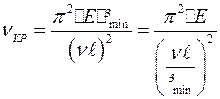где – минимальный радиус инерции определяемый из 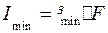, или ,

где 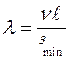– безразмерная величина, называемая гибкостью стержня и характеризующая его способность сопротивляться искривлению в зависимости от размеров и способа закрепления концов (шарнирно, жестко, консольно).

Условие устойчивости при этом будет:

, (6.5)

где 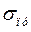– предел пропорциональности (табличные данные).

На практике используют более простую зависимость:

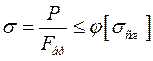, (6.6)

где – коэффициент предельного изгиба;

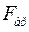– площадь поперечного сечения полная (брутто).

Дата добавления: 2014-12-16