Примеры расчетов систем на жесткость

Исходные данные и постановка задач

Пример 1 (статически определимая система) Стальной брус постоянного сечения F и длиной , защемленный обоими концами, подвержен действию силы P, приложенной на расстояние , от верхнего конца и от нижнего конца (рисунок 2.3). Необходимо определить усилия, действующие в частях бруса и .

Решение. Вертикальная сила Р растягивает верхнюю часть бруса и сжимают нижнюю в связи с чем реакции R_А и R_В в зацеплениях из уравнений статики определены быть не могут, т.к. при двух неизвестных может быть составлено только одно уравнение или равновесие:

(2.16)

Рисунок 2.3

Второе уравнение получаем из рассмотрения деформации бруса. Так как концы бруса защемлены, длина его изменяться не может и, следовательно, суммарное абсолютное удлинение верхней и нижней частей бруса равно нулю, т.е. удлинение верхней части, растягиваемой силой , равно укороченной нижней части, сжимаемой силой . отсюда согласно (2.15):

, или

(2.17)

Решая уравнения (2.16) и (2.17) совместно, получим:

Пример 2 (статистически неопределимая система). Напряжения, вызванные изменением температуры. Рассмотрим два стержня, первый из которых (рисунок 2.4, а) закрепили одним концом и представляет статически неопределимую систему, а второй (рисунок 2.4, б) защемлен двумя концами, т.е. является системой статически определенной. Пусть стержни подвергнуты нагреву от температуры t₀ до температуры t₁. определить внутреннее напряжение во втором стержне.

Решение. Длина первого стержня изменится на длину , где - коэффициент линейного расширения, равный для стали 1/град., 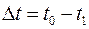, - перепад температур; 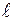- первоначальная длина стержня.

Рисунок 2.4

В этом стержне не возникает внутренних сил напряжений, т.к. отсутствует препятствие для перемещения его свободного конца (при температурном расширении).

Во втором случае в стержне возникает внутреннее сжимающее усилие, т.к. зацепка по концам препятствует удлинению стержня при нагреве.

Таким образом в статически определенных системах (рисунок 2.4,а) при изменении температуры (нагреве) возникают деформации без появления внутренних усилий, а в статически неопределимых системах (рисунок 2.4,б) изменение температуры сопровождается появлением внутренних усилий, следовательно, напряжений.

Определим напряжение в стержне, защемленным двумя концами и подверженном нагреву от температуры t₀, при которой произведено защемление, до температуры t₁ (рисунок 2.4,б).

При нагревании стержня он будет удлиняться и оказывать давление на опорные поверхности 1 и 2. это приведет к возникновению усилий R₁ и R₂, сжимающих стержень. Из условия равновесия этих сил следует: R₁= R₂= R.

Величина сжимающей силы остается неизвестной. Определим сжимающее усилие из условия деформации. При этом рассуждаем так:

Если бы один конец был свободен, стержень удлинился бы при нагревании на величину:

Однако, наличие двух неподвижных … исключает перемещение концевых сечений, поэтому ,т.е.

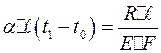
Отсюда: ,

а напряжение, возникающее в стержне будет:

Величина температурных напряжений в некоторых случаях может оказаться весьма значительной. Для уменьшения температурных напряжений в конструкциях (например, мостовых) предусматривают специальные температурные зазоры, не допускающие излишних напряжений.

Дата добавления: 2014-12-16