Физический смысл производной

Уравнение касательной и нормали.

Ш уровень

3.1. Найдите производную функции:

1) ; 2) ;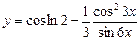

3) ;

4) .

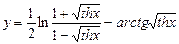3.2. Найти производную функции, предварительно преобразовав выражение по тригонометрическим формулам:

1) ; 2) ;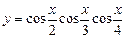

3) ;

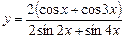4) ;

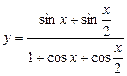
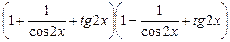5) .

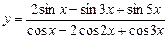6) .

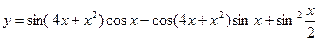3.3. Дана функция 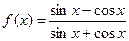Определите, чему равно значение выражения .

3.4. Даны функци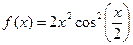и и . Найдите количество значений на отрезке 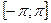, для которых выполняется равенство .

Производная функции 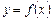в точке 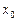представляет собой угловой коэффициент касательной, проведённой к графику функции в точке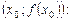

где 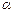- угол наклона касательной к оси Ox. В этом состоит геометрический смысл производной.

Уравнение касательной, проведённой к графику функции в точк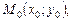е где имеет вид

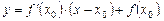(9)

Прямая, проходящая через точку 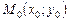графика функции 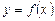перпендикулярно касательной, проведённой в этой точке, называется нормалью к графику функции 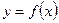в точке 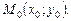Уравнение нормали имеет вид

(10)

где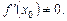

Физические приложения производной

1. Если материальная точка M движется неравномерно по пути, заданному функцией , то мгновенная скорость движения в момент времени 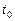есть производная от пути S по времени t:

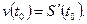(11)

2. Если функцией 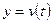описывается процесс изменения скорости неравномерного движения в зависимости от времени, то мгновенное ускорение материальной точки в момент времени 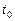есть производная от скорости 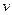по времени t:

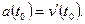(12)

3. Если 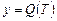– функция, описывающая процесс изменения количества теплоты, сообщаемой телу при нагревании его до температуры T, то теплоёмкость тела есть производная от количества теплоты Q по температуре T:

4. Линейная плотность неоднородного тонкого стержня в точке 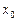есть производная от массы m по длине l:

5. Мгновенное значение электродвижущей силы индукции равно скорости изменения магнитного потока, т.е. производной от магнитного потока 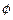по времени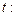

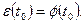
6. Сила тока в колебательном контуре в момент времени 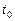равна производной заряда по времени :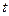

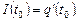
Пример 1. Написать уравнение касательной и нормали, проведённой к графику функции в точке с абсциссой x = 2.

Решение. Для нахождения уравнения касательной воспользуемся формулой (9). Сначала найдём ординату точки касания 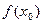. Для этого значение 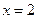подставим в уравнение функции:

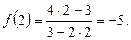
Для нахождения углового коэффициента найдём производную 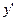, используя формулу дифференцирования дроби:

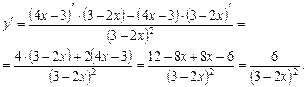
Найдём значение производной при :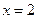

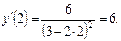
Подставляем найденные значения в формулу (9), получаем уравнение касательной:

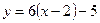, т.е.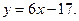

Чтобы написать уравнение нормали, воспользуемся формулой (10):

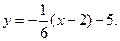
Получим, что уравнение нормали, проведенной к заданной кривой в заданной точке имеет вид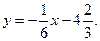

Пример 2. Определить, в какой точке кривой 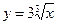касательная наклонена к оси абсцисс под углом 45°.

Решение. Так как тангенс угла наклона касательной к оси абсцисс равен значению производной в точке касания, найдём производную функции:

.

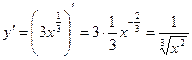По условию Значит, .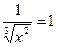

Отсюда

, , .

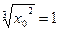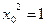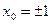Получили два значения абсциссы точки касания:

, ,

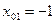т.е. существует две точки касания, в которых касательная образует угол 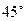с осью .

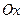Найдём соответствующие ординаты точек касания, подставляя значения в формулу функции:

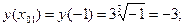
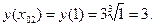
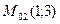Приходим к ответу: в точках и касательная к заданной кривой образует с осью 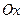угол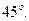

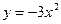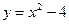Пример 3. Найти острый угол между параболами и в точке их пересечения, имеющей отрицательную абсциссу.

Решение. Угол между двумя кривыми в точке их пересечения - это угол между касательными к этим кривым, проведёнными в точке их пересечения. Тангенс этого угла вычислим по формуле:

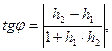(13)

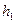где и 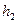-угловые коэффициенты заданных парабол.

Найдём точку пересечения этих парабол. Для этого решим систему:

Отсюда 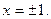Условие задачи удовлетворяет точка 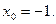Найдём коэффициент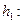

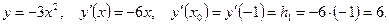Аналогично найдём :

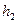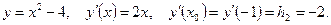
Воспользуемся формулой и получим:

,

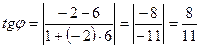откуда

Пример 4. Тело движется прямолинейно по закону 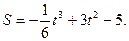Найти скорость движения тела в тот момент, когда ускорение равно нулю.

Решение. Согласно формуле (11) скорость есть производная пути, а, согласно формуле (12), ускорение есть производная от скорости.

Последовательно вычислим производные:

Найдём момент времени, когда ускорение равно нулю:

Вычислим скорость движения тела в момент времени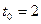

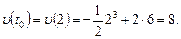
Задания для самостоятельного решения.

Дата добавления: 2014-12-16