Магнитная энергия двух контуров с токами

Магнитная энергия поля.

Рассмотрим бесконечно длинный соленоид, индуктивность которого , тогда

Так как

Формула получена для однородного магнитного поля.

Энергия магнитного поля локализована в пространстве и распределена по пространству с объёмной плотностью Над плотностью нужно поставить чёрточку (знак вектора).

Возьмём 2 неподвижных контура 1 и 2, расположив их достаточно близко друг к другу (чтобы была магнитная связь). Предположим, что в каждом контуре есть своя постоянная ЭДС. Замкнём в момент t = 0 оба контура. В каждом из них начнёт устанавливаться ток, появится ЭДС самоиндукции и ЭДС взаимной индукции .

Дополнительная работа, совершаемая источниками постоянной ЭДС, идёт на создание магнитной энергии (против ЭДС самоиндукции и взаимной индукции).

Найдём эту работу за время dt:

После подстановки будем иметь:

Учтём, что

Отсюда:

Первые 2 слагаемых называются собственной энергией тока 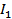и тока , последнее – взаимной энергией обоих контуров.

Вычислим энергию 2-х контуров несколько иначе – с точки зрения локализации энергии в поле.

Пусть - вектор магнитной индукции поля тока I₁, - вектор магнитной индукции поля тока I₂.

Тогда энергия поля этой системы:

Формулы (1) и (2) приводят к таким важным следствиям.

Магнитная энергия системы токов величина всегда положительная.

Энергия токов величина положительная.

Последний интеграл пропорционален произведению токов , так как , .

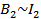Последний интеграл оказывается симметричным относительно индексов 1 и 2, его можно обозначить и 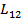как и как , так как L₁₂=L₂₁.

Сопоставление выражений (1) и (2) показывает, что

40.Напряжённость магнитного поля. Теорема о циркуляции вектора Н.

Напряжённость магнитного поля (стандартное обозначение Н) — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M.

Циркуляция вектора H по любому замкнутому контуру равна полному току через произвольную поверхность, ограниченную данным контуром.

39. Магнитное поле в веществе. Намагниченность. Токи намагничивания.

Если вещество внести в магнитное поле, то оно намагнитится, связано это с тем, что магнитное поле воздействует на круговые молекулярные токи, ориентируя их по направлению внешнего магнитного поля. В результате, внутри вещества возникает собственное магнитное поле .

Результирующее магнитное поле в соответствии с принципом суперпозиции:

Речь идёт о полях, усреднённых по физически бесконечно малому объёму. Поле B’ так же как и поле B₀ является вихревым. Поэтому и при наличии магнетика справедлива теорема Гаусса:

Намагниченность

Степень намагничивания магнетика характеризуют магнитным магнитом единицы объёма. Эту величину называют намагниченностью

- физически бесконечно малый объём в окрестности данной точки,

- магнитный момент отдельной молекулы.

Вектор - аналогичен вектору для него также справедливо представление:

n – концентрация молекул, – средний магнитный момент одной молекулы.

Токи намагничивания

При внесении магнетика в магнитное поле, малые токи ориентируются таким образом, чтобы их магнитные моменты были направлены по полю, то есть, совпадали бы по направлению с вектором намагничивания

Из рисунка видно, что у соседних молекул внутри магнетика молекулярные токи текут в противоположных направлениях и таким образом компенсируют друг друга. Не скомпенсированными остаются токи, выходящие на поверхность магнетика. Такие токи называются токами намагничивания. Токи намагничивания могут возникнуть также в объёме магнетика, если он неоднороден. В таком случае молекулярные токи в различных местах магнетика различны. Этот факт отобразим толщиной кругового тока.

Дата добавления: 2014-12-16