Изосова Л.А., Изосов А.В. 3 страница

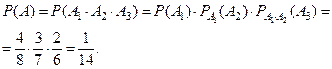
Введём понятия зависимых и независимых событий.

Рассмотрим опыт из примера 2 предыдущего параграфа, но произведём его следующим образом: извлекаем один шар из урны с 6 – ю белыми и 4 – мя чёрными шарами, определяем его цвет, возвращаем его в урну, перемешиваем шары и снова извлекаем один шар. При тех же обозначениях вероятность того, что оба шара белые, равна

.

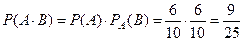Здесь мы столкнулись с понятием независимых событий.

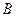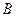Определение. Событие называется независимым по отношению к событию , если ероятность события не зависит от того, произошло событие или нет, т.е. 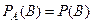. В противном случае, событие 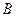называется зависимым от события .

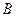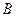В примере 2 предыдущего параграфа событие зависело от события (в урне изменилось количество шаров). В примере, рассмотренном выше, при повторном извлечении шара начальные условия не изменились, поэтому вероятность события не зависит от того, произошло событие или нет, т.е. событие 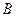не зависит от события .

Замечание. Если событие 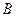не зависит от события , то и событие не зависит от события .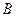

В самом деле, из аксиомы 5,

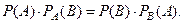
Но 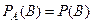. Тогда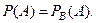

Определение. Два события называются независимыми, если появление одного из них не меняет вероятность появления другого.

Понятие независимости можно распространить на случай произвольного числа событий.

Определение. Несколько событий называются независимыми в совокупности если каждое из них и любая комбинация ос -тальных событий являются независимыми.

Например, события 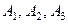независимы в совокупности, если независимы друг относительно друга следующие события: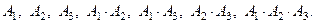

Следствие (теоремы об умножении вероятностей). Вероятность произведения независимых в совокупности собы -тий равна произведению их вероятностей, т.е.

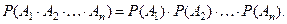
(При условии независимости событий, условные вероятности в формуле (1) меняются на безусловные вероятности, в соответ-ствии с условием независимости событий).

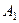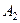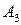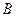Пример 1. Произведено 3 выстрела по удаляющейся мише -ни. Вероятность попадания при первом выстреле (событие ) равна 0,9, при втором (событие ) - 0,7, при третьем (собы- тие ) - 0,5. Найти вероятности следующих событий: - «все три попадания»; - «ровно два попадания»; 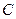- «толь- ко одно попадание»; 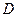- «по крайней мере два попадания»; 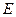- «хотя бы одно попадание»; 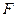- «ни одного попадания» (предполагается, что исходы всех выстрелов независимы друг от друга). Следовательно, 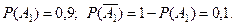Аналогично,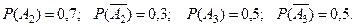

В данных условиях, 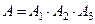. События 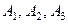независимы. Тогда

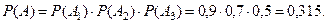
Событие 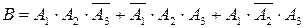. Все слагаемые, входящие в событие 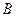- несовместны, а множи -тели слагаемых - независимы. Поэтому

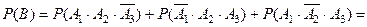
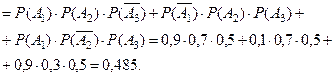
Событие

.

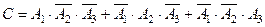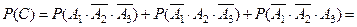
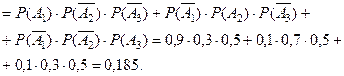
Событие:

,

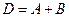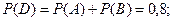
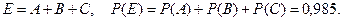
Событие 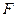можно представить двумя способами: либо

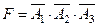и тогда его вероятность равна

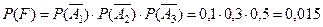, либо , тогда, учитывая следствие 2 теоремы о сложении вероятнос -тей,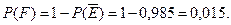

Двумя способами получили тот же результат.

Пример 2. 5 раз подбрасывается монета. Найти вероят –ность того, что все 5 раз она выпадет одной и той же сто- роной (событие ), либо все 5 раз выпадет герб (событие 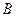), либо все 5 раз выпадет цифра (событие 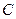). . 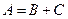Со -бытия 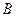и 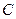несовместны. Поэтому .

Подбрасывания монеты считаем независимыми. Вероятность появления герба (цифры) при каждом подбрасывании равна 0,5. Тогда

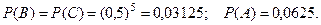
Теорема. (теорема о сложении вероятностей совместных со- бытий) Вероятность появления хотя бы одного из двух сов- местных событий равна сумме их вероятностей без вероят -ности их совместного появления, т.е.

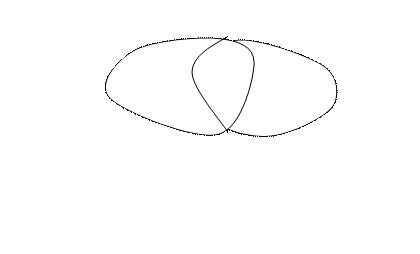
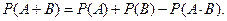
Д о к а з а т е л ь с т в о. Рассмотрим рисунок:

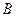
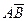
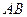
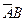
События 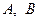и 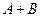можно представить следующим обра- зом: 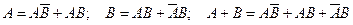. Слагаемые, входящие в эти события, являются несовместными. По правилу сложения вероятностей несовместных событий (ак- сиома 4), получаем:

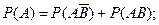
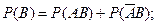
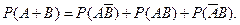Поэтому, так как

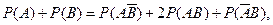
получаем

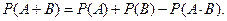
Теорема доказана.

Замечание. Если искать вероятность суммы трёх совмест -ных событий, то получим формулу:

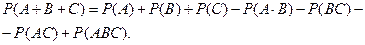
По мере увеличения числа слагаемых формула сложения ве -роятности совместных событий довольно быстро разрастается и приводит к громоздким вычислениям, что очень неудобно. Поэтому при вычислении верояности суммы нескольких сов -местных событий целесообразно использовать понятие веро -ятности противоположного события. Если событие 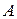- «появ- дение хотя бы одного из совместных событий 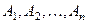», т.е. 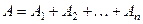, то вероятность этого события мож- но вычислить следующим образом:

Это формула вычисления вероятности появления хотя бы одного из 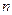совместных событий.

Пример 1. Два раза подбрасывается игральный кубик. Найти вероятность того, что хотя бы один раз выпадет цифра 5.

- цифра 5 при первом подбрасывании. 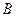- цифра 5 при втором подбрасывании. 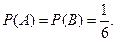Тогда, по теореме,

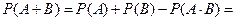
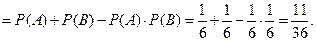
Другим способом, 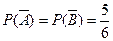. Тогда

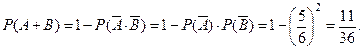
Получили тот же результат.

Пример 2. Произведено 3 выстрела по удаляющейся мише - ни. Вероятность попадания при первом выстреле (событие 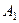) равна 0,9, при втором (событие 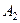) - 0,7, при третьем (собы- тие 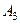) - 0,5. Найти вероятность хотя бы одного попадания в мишень.

Воспользуемся формулой

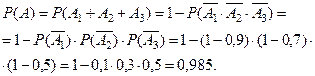
§ 7. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ, ФОРМУЛА

БЕЙЕСА).

Пусть имеется полная группа несовместных событий - гипо- тез - 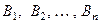, для которых известны их вероятности. Тогда, по следствию 1 из теоремы о сложении вероятностей, сумма их вероятностей равна 1, т.е. .

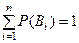Пусть некоторое интересующее нас событие 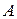может прои -зойти или не произойти в случае выполнения одной из гипотез 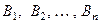и известны условные вероятности появления события при выполнении каждой из гипотез: 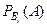. Тогда вероятность события 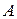определяется по формуле: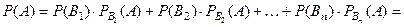 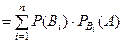. (1)

Эта формула называется формулой полной вероятности.

В самом деле, событие можно представить следующим образом: 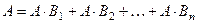. Так как события

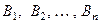несовместны, то входящие в событие слагаемые также несовместны, т.е. 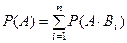. По аксиоме умножения вероятностей, 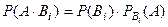и тогда: 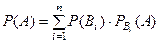. Получили нужную формулу.

Пример 1. Три станка – автомата, производительности кото -рых относятся как 3: 2: 5 штампуют одинаковые детали. 80% деталей, изготовленных 1 – м станком, 90%, изготовленных 2 – м станком, и 70%, изготовленных 3 – м станком, являются стан –дартными. Все изготовленные детали хранятся в одном ящике. Найти вероятность того, что взятая наугад деталь окажется стандартной.

Событие - «даталь стандартная» зависит от событий 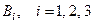(т.е. от того, каким станком была изготовлена детпль). Вероятности этих событий, учитывая производитель- ности станков – автоматов, равны, соответственно,

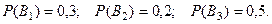
Условные вероятности появления события определяются процентами стандартных деталей для каждого станка, т.е.

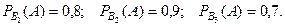
Тогда, по формуле полной вероятности (1),

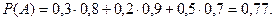
Пример 2. Пусть в первой урне находится 8 белых и 12 синих шаров, во второй урне - 5 белых и 3 синих шара. Из первой урны произвольным образом извлекаются 2 шара и перекладываются во вторую урну. Затем из второй урны из- влекается один шар. Найти вероятность того, что извлечённый шар белый (событие ).

Событие зависит от того, какие шары были добавлены во вторую урну, т.е. от событий 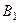- «два белых шара», 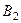- «белый и синий шар», событие - «два синих шара». Най – дём вероятности этих событий:

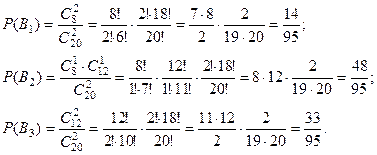Условные вероятности события 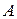по каждому из этих со -бытий равны, соответственно,

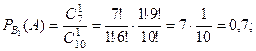
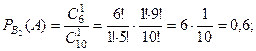
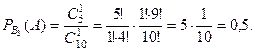
Тогда вероятность события равна

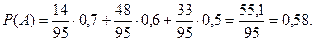
Замечание. Формула полной вероятности - это следствие теоремы сложения вероятностей и аксиомы умножения вероят- ностей.

Поставим теперь следующую задачу. Пусть имеется полная групппа несовместных событий - гипотез - 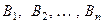, для которых известны их вероятности 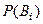, 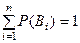. Пусть некоторое интересующее нас событие может произой- ти или не произойти в случае выполнения одной из этих ги -потез и известны условные вероятности появления события при выполнении каждой из гипотез: 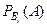. По формуле пол- ной вероятности (1) мы можем найти вероятность события . Пусть событие произошло. Требуется определить долю участия каждой из гипотез в выполнении события , т.е. най- ти вероятности: 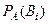. Эти вероятности можем найти по следующей формуле:

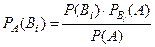. (2)

Эта формула называется формулой Бейеса.

В самом деле, из аксиомы умножения вероятностей,

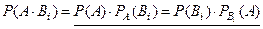эта формула получается автоматически.

Пример 3. В условиях примера 1 этого параграфа, опреде – лить вероятность того, что выбранная стандартная деталь из -готовлена 1 – м станком.

По формуле (2),

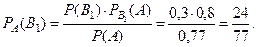
Пример 4. Четыре машинистки в течение определённого времени печатают рукопись в 300 счтраниц. Первая из них напечатала 60 страниц, вторая - 80, страниц, третья - 110 страниц, четвёртая - 50 страниц. Вероятность сделать опе - чатку для первой машинистки равна 0,2, для второй - 0,3, для третьей - 0,1 и для четвёртой - 0,4. После сверки текста была обнаружена опечатка. Какая машинистка, вероятнее все -го сделала опечаику.

В условиях этой задачи: событие 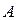- опечатка в тексте, события 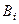- опечатка была сделана 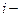й машинисткой .

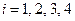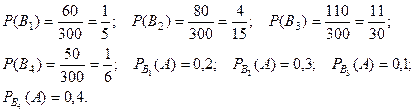Тогда вероятность ошибки в рукописи:

Теперь, воспользуясь формулой Бейеса, оценим вероятности:

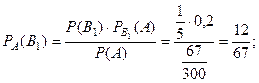
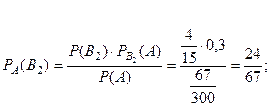
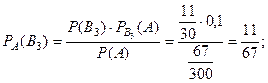
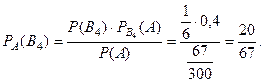
Таким образом, вероятнее всего опечатку сделала вторая машинистка.

§ 8. ПОВТОРЕНИЕ ИСПЫТАНИЙ. ФОРМУЛА БЕРНУЛЛИ.

Пусть произведено 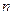испытаний. Если вероятность собы -тия в каждом испытании не зависит от результатов других испытаний, то такие испытания называются независимыми от– носительно события

Для серии таких испытаний может быть поставлена следу -ющая задача: определить вероятность того, что в результате проведения 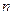независимых испытаний, в которых событие появляется с постоянной вероятностью 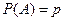, событие произойдёт ровно 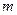раз, т.е. найти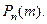

При условии 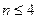можно было бы воспользоваться теоремами сложения и умножения вероятностей с исполь- зованием правил сложения и уножения вероятностей событий. Но, по мере увеличения числа испытаний, эти правила приводят к громоздким формулам и, с учётом перебора возможных вариантов, к не менее громоздким вычислениям.

Более простой способ вычисления таких вероятностей осно- ван на применении формулы Бернулли.

Пусть в одинаковых условиях производится 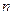независимых испытаний, в каждом из которых событие появляется с по- стоянной вероятностью 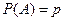, а противоположное собы -тие 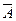с вероятностью .

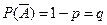Пусть 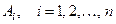- появления события в 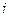- м испытании ().

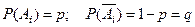Рассмотрим такое событие: в 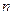испытаниях первые 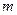раз событие появилось, а потом перестало появляться, т.е. со- бытие 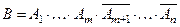. Так как входящие в собы -тие 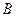события независимы, то

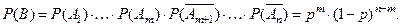Но комбинаций, типа комбинации 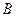, существует 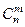(т.е. столько есть способов расставить « 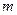чёрточек над 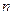множи - телями»), причём все такие комбинации несовместны. Поэтому

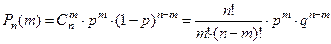. (1)

Полученная формула называется формулой Бернулли.

Пример 1. В среднем пятая часть поступающих в продажу автомобилей некомплектна. Найти вероятность того, что среди 10 – ти прибывших автомобилей имеют некомплектность: а) три автомобиля; б) хотя бы три.

Событие - автомобиль имеет некомплектность. Тогда, по условию,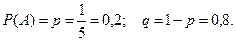

а) По формуле (1),

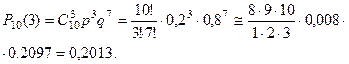
б) Событие 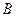- «хотя бы три автомобиля некомплектны», те. от 3 – х до 10 – ти. Его вероятность проще искать через вероятность противоположного событие 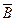- «менее 3 – х ав- томобилей некомплектны».

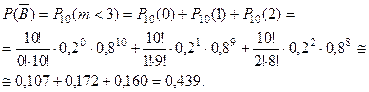Тогда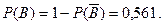

Так как события, состоящие в различном числе появлений события в серии из 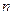независимых испытаний образуют полную группу несовместных событий, то сумма их вероят -ностей равна единице, т.е.

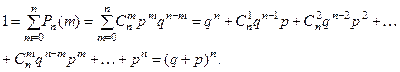
Эта сумма представляет собой разложение 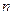- й степени бинома (бином Ньютона) и связанное с ней распределение вероятностей числа появлений события 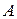в серии из 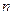опытов называется биномиальным распределением.

Учмтывая это, для вычисления вероятностей возможного числа появлений события 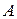в серии из 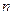независимых ис- пытаний можно ввести так называемую производящую функ- цию:

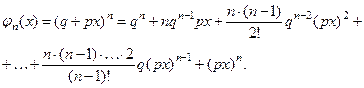
Эта функция обладает тем свойством, что коэффициент, стоя- щий перед 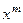в этой сумме равен вероятности .

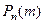Пример 2. Предполагается, что в среднем 20% открываю –щихся малых предприятий разоряются в течение года. Найти вероятность того, что после года работы из 6 – ми вновь от - крывшихся предприятий не разорится: а) ровно 5; б) хотя бы четыре.

Вероятность того, что предприятие разорится 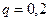, со - ответственно, вероятность того, что оно не разорится, равна 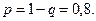Для решения воспользуемся производящей функцией.

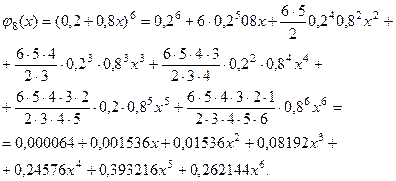Непосредственным сложением можем проверить, что сумма всех коэффициентов в этом разложении равна 1. Тогда, в случае а): 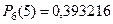, т.е. коэффициент, стоящий перед 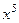. В случае б): 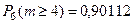, т.е. сумма коэффициен- тов, стояший перед .

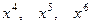Дата добавления: 2014-11-29