Случайные величины 1 страница

§ 1. ПОНЯТИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ.

В физике и других науках о природе встречается много различных величин разной природы, как например: время, длина, объём, вес и т.д. Постоянной величиной называют ве- личину, принимающую лишь одно фиксированное значение. Величины, которые могут принимать различные значения, на-зываются переменными. Величина считается заданной, если указано множество значений, которые она может принимать. Если однозначно известно, какое именно значение из множества примет величина при создании опреде- лённых условий, то о ней говорят как об «обычной», детерминированной величине. Примером такой величины является количество букв в слове. Большинство физических величин измеряются при помощи приборов с присущей им точностью измерений и, в смысле приведенного определения, они не являются «обычными». Такого рода «необычные» величины называются случайными. Для случайных величин множество 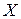целесообразно назвать множеством возможных значений. Случайная величина принимает то или иное значе- ние с некоторой вероятностью. Заметим, что все величины можно считать случайными, так как детерминированная вели-чина – это случайная величина, принимающая каждое значение с вероятностью, равной единице. Всё сказанное выше является достаточным основанием для изучения случайных величин.

Определение. Случайной величиной называется величина, которая в результате опыта может принимать то или иное (но обязательно только одно) значение, причём заранее, до опыта, неизвестно, какое именно.

Понятие случайной величины является фундаментальным понятием теории вероятностей и играет важную роль в её приложениях.

Случайные величины обозначаются: , а их зна -чения, соответственно: .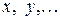

Выделяют два основных класса случайных величин: диск -ретные и непрерывные.

Определение. Дискретной случайной величиной называют случайную величину, число возможных значений которой конечное либо счётное множество.

Примеры дискретных случайных величин:

1. 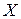- частота попаданий при трёх выстрелах. Возможные значения:

2. 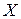- число деффектных изделий из 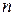штук. Возможные значения: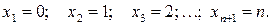

3. 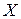- число выстрелов до первого попадания. Возможные значения: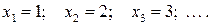

Определение. Непрерывной случайной величиной называют такую случайную величину, возможные значения которой не –прерывно заполняют некоторый промежуток (конечный или бесконечный).

Примеры непрерывных случайных величин:

1. 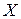- случайное отклонение по дальности от точки попада- ния до цели при выстреле из орудия.

Так как снаряд может попасть в любую точку, интервала, ограниченного минимальным и максимальным значениями дальности полёта снаряда, возможных для данного орудия, то возможные значения случайной величины 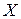заполняют про -межуток между минимальным и максимальным значением.

2. 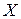- ошибки при измерении радиолокатором.

3. 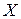- время работы прибора.

Случайная величина является своего рода абстрактым вы- ражением некоторого случайного события. С каждым случай -ным событием можно связать одну или несколько характеризу- ющих его случайных величин. Например, при стрельбе по ми -шени можно рассмотреть такие случайные величины: число попаданий в мишень, частота попаданий в мишень, количество очков, набираемых при попадании в определённые области мишени и т.д.

§ 2 ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ

СЛУЧАЙНЫХ ВЕЛИЧИН.

Определение. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь меж- ду возможными значениями случайной величины и соответст- вующими им вероятностями.

Если вспомнить определение функции, то закон распреде -ления является функцией, область определения которой есть область значений случайной величины, а область значений рассматриваемой функции состоит из вероятностей значений случайной величины.

2.1. РЯД РАСПРЕДЕЛЕНИЯ

Рассмотрим дискретную случайную величину , воз- можные значения которой 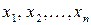нам известны. Но зна- ние значений случайной величины, очевидно, не позволяет нам её полностью описать, так как мы не можем сказать, насколь- ко часто следует ожидать тех или иных возможных значений случайной величины при повторении опыта в одних и тех же условиях. Для этого необходимо знать закон распределения вероятностей.

В результате опыта дискретная случайная величина прини –мает одно из своих возможных значений, т.е. произойдёт одно из событий:

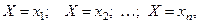(1)

которые образуют полную группу несовместных событий.

Вероятности этих событий:

,

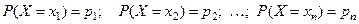Простейшим законом распределения дискретной случайной величины является таблица, в которой приведены все возмож- ные значения случайной величины и соответствующие им ве –роятности:

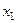
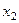
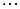
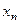
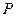
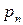
Такую таблицу называют рядом распределения случайной величины .

Для наглядности, ряд распределения можно представить графиком:

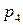
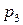
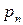
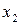
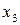
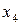
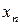
Эта ломаная называется многоугольником распределения. Это также одна из форм задания закона распределения дискрет – ной случайной величины .

Сумма ординат многоугольника распределения, представля – ющая сумму вероятностей всех возможных значений случай -ной величины, равна единице.

Пример 1. Произведено три выстрела по мишени. Вероят- ность попадания при каждом выстреле равна 0,7. Составить ряд распределения числа попаданий.

Случайная величина - «число попаданий» может прин- мать значения от 0 до 3 – х, причём в этом случае вероят – ности определяются по формуле Бернулли:

.

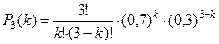Тогда

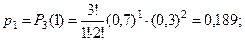
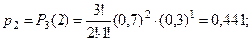
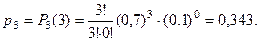
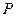
	0,027	0,189	0,441	0,343

Проверка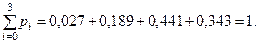

Пример 2. В урне назодится 4 белых и 6 чёрных щаров. Наугад извлекаются 4 шара. Найти закон распределения слу- чайной величины - «число белых шаров среди отобран -ных».

Эта случайная величина может принимать значения от 0 до 4 – х. Найдём вероятности аозможных значений случайной величины.

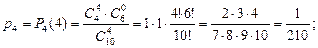
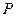
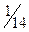
Можем проверить, что сумма полученных вероятностей рав- на единице.

2.2. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ.

Ряд распределения нельзя построить для непрерывной слу- чайной величины, так как она принимает бесконечно много значений. Более универсальным законом распределения под- ходящим, как для дискретной, так и для непрерывной слу - чайной величины является функция распределения.

Определение. Функцией распределения (интегральным зако- ном распределения) случайной величины называется зада- ние вероятности выполнения неравенства 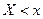, т.е.

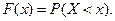(1)

Таким образом, функция распределения 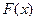равна вероят -ности того, что случайная величина в результате опыта попа- дает левее точки .

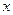Для дискретной случайной величины, для которой мы знаем ряд распределения:

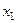
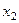
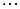
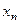
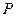
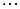
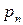
функция распределения будет иметь вид:

График функции распределения дискретной случайной вели- чины - разрывная ступенчатая фигура. Для наглядности, рассмотрим пример.

Пример 3 Дан ряд паспределения. Найти функцию распре -деления и построить её график

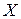
	0,2	0,1	0,3	0,4

По определению,

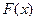
0,8

0,3

0,2

1 2 3 4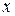

СВОЙСТВА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ

1 Функция распределения - это неотрицательная фун- кция, значения которой заключены между 0 и 1, т.е.

2 Вероятность появления случайной величины в про- межутке равна разности значений функции распределения на концах промежутка:

(2)

3 Функция распределения - неубывающая функция, т.е. при 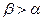выполнено: ;

4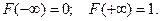

Перейдём в равенстве (2) к пределу при 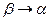. Полу- чим вместо вероятности попадания случайной величины в про- межуток 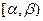вероятность точечного значения случайной величины, т.е.

. (3)

Значение этого предела зависит от того, является ли точка 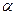точкой непрерывности функции 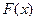, или в этой точке функция 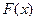имеет разрыв. Если функция 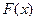непрерыв- на в точка 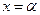, то предел равен 0, т.е. 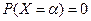. Если же в этой точке функция 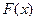имеет разрыв (1 – го ро- да), то предел равен значению скачка функции 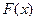в точке .

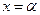Так как непрерывная случайная величина имеет непрерыв -ную функцию распределения 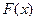, то из равенства нулю предела (3) следует, что вероятность любого фиксированного значения непрерывной случайной величины равна нулю. Это следует из того, что возможных значений непрерывной случайной величины бесконечно много. Из этого, в частности, следует, что следующие вероятности совпадают:

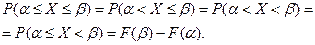
Приведённые свойства функции распределения можно сфор- мулировать следующим образом: функция распределения - это неотрицательная неубывающая функция, удовлетворяющая ус –ловиям: 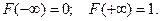Обратное утверждение также имеет место: монотонно возрастающая непрерывная функция, удовлетворяющая условиям

является функцией распределения некоторой непрерывной слу- чайной величины. Если значения этой величины сосредоточе -ны на некотором промежутке , то график этой функции можно схематически изобразить следующим образом:

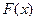
0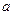

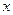
Рассмотрим пример. Функция распределения непрерывной случайной величины задана следующим образом:

Найти значение «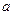», построить график 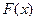и найти веро –ятность

Так как функция распределения непрерывной случайной ве- личины непрерывна, то 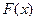- непрерывная функция, и при должно выполгяться равенство:

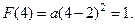или , т.е.

Построим график этой функции

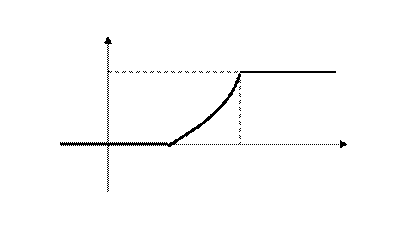
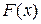
0 2 4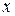

Найдём требуемую вероятность

Замечание. Функцию распределения, иногда ещё называют интегральным законом распределения. Ниже объясним, почему именно.

2.3 ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ.

Так как с помощью функции распределения дискретной

случайной величины в любой точке мы можем определить вероятность возможных значений, то она однозначно опре- деляет закон распределения дискретной случайной величины.

Однако по функции распределения трудно судить о харак- тере распределения непрерывной случайной величины в не -большой окрестности той или иной точки числовой оси.

Более наглядное представление о характере распределения непрерывной случайной величины вблизи различных точек даёт функция, которую называют плотностью распределения (или дифференциальным законом распределения)

Пусть - непрерывная случайная величина с функцикй распределения 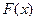. Найдём вероятность попадания этой случайной величины в элементарный участок .

По формуле (2), имеем

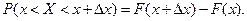
Разделим это равенство на

.

Отношение, стоящее слева, называется средней вероятно –стью на единице длины участка.

Считая функцию 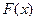дифференцируемой, перейдём к перейдём в этом равенстве к пределу

.

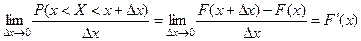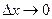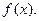Определение. Предел отношения вероятности попадания непрерывной случайной величины на элементарный участок к длине этого участка при называ- ется плотностью распределения непрерывной случайной ве – личины и обозначается Следовательно,

Плотность распределения показывает, насколько часто слу -чайная величина 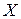появляется в некоторой окрестности точ –ки 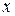при повторении опытов.

Кривая, изображающая график плотности распределения, на- зывается кривой распрелеления.

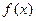
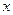
Если возможные значения случайной величины запол- няют некоторый промежуток 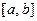, то 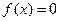вне этого промежутка.

Определение. Случайная величина называется непре – рывной, если её функция распределения 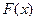непрерывна на всей числовой прямой, а плотность распределения 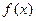не- прерывна везде, за исключением может быть конечного числа точек (точек разрыва 1 – го рода).

СВОЙСТВА ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ

1. Плотность распределения неотрицательна, т.е.

(это следует из того, что 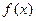- производная неубывающей функции ).

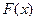2. Функция распределения непрерывной случайной величи-

ны равна интегралу от плотности распределения (и поэтому является интегральным законом распределения), т.е.

В самом деле, 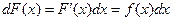(по определению дифференциала функции). Следовательно,

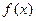
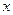
На графике плотности распределения функция распределения

изображается площадью заштрихованной области.

3. Вероятность попадания случайной величины на участок 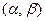равна интегралу от плотности распределения по этому промежутку, т.е.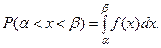

В самом деле,

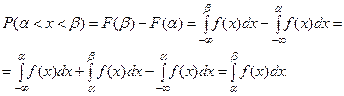
4. Интеграл в бесконечных пределах от плотности распре –деления равен единице, т.е.

Другими словами, площадь фигуры под графиком плотности распределения равна 1. В частности, если возможные значе- ния случайной величины сосредоточены на участке , то

Пример. Пусть плотность распределения зазана функцией

Найти: а) значение параметра ; б) функцию распределения в) Вычислить вероятность того, что случайная величи- на примет значение из отрезка .

а) По свойству 4, . Тогда

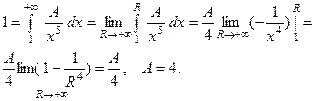
б) По свойству 2, Если

Если , .

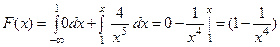Таким образом,

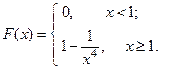
в) По свойству 3,

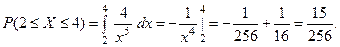
§ 3. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ

ВЕЛИЧИН

При решении многих практических задач нет необходимости знать все вероятностные характеристики случайной величины. Иногда достаточно знать только некоторые числовые характе - ристики закона распределения.

Дата добавления: 2014-11-29