Случайные величины 2 страница

Числовые характеристики позволяют в сжатой форме выра -зить наиболее существенные особенности того или иного рас- пределения.

О каждой случайной величине прежде всего необходимо знать её среднее значения, около которого группируются все возможные значения этой величины, а также некоторое число, характеризующее степень рассеяния этих значений относитель- но среднего.

Различают характеристики положения и характеристики рас- сеяния. Одной из самых важных характеристик положения яв- ляется математическое ожидание.

3.1 Математическое ожидание (среднее значение).

Рассмотрим сначала дискретную случайную величину, име -ющую возможные значения 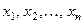с вероятностями

.

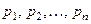Определение. Математическим ожиданием дискретной слу- чайной величины 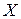называется сумма произведений всех возможных значений этой величины на их вероятности, т.е.

. (1)

По другому, математическое ожидание обозначается

Пример. Пусть дан ряд распределения:

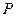
	0,2	0,1	0,3	0,4

Тогда

Рассмотрим теперь непрерывную случайную величину все возможные значения которой заключены в отрезке .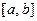

Разобьём этот отрезок на 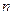частичных отрезков, длины которых обозначим: 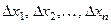, и в каждом частичном интервале возьмём по произвольной точке, соответственно .

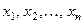Так как произведение 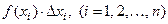при- ближённо равно вероятности попадания случайной величины на элементарный участок , то сумма произведений составленная по аналогии с опреде -лением математического ожидания дискретной случайной ве- личины, приближённо равна математическому ожиданию не -прерывной случайной величины 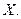Пусть .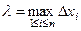

Тогда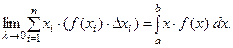

Определение. Математическим ожиданием непрерывной случайной величины называется следующий определённый интеграл:

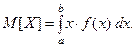(2)

Если непрерывная случайная величина принимает значения на всей числовой прямой, то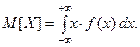

Пример. Пусть дана плотность распределения непрерывной случайной величины:

Тогда её математическое ожидание:

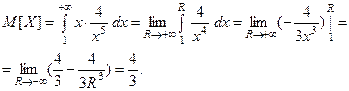
Понятие математического ожидания имеет простую меха -ническую интерпретацию. Распределение вероятностей слу -чайной величины можно интерпретироварь как распределение единичной массы по прямой. Дискретной случайной величине, принимающей значения 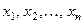с вероятностями 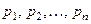соответствует прямая, на которой массы 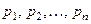сосредоточены в точках 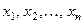. Непре- рывной случайной величине отвечает непрерывное распреде -ление масс на всей прямой или на конечном отрезке этой прямой. Тогда математическое ожидание - это абсцисса цент- ра тяжести.

СВОЙСТВА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ

1. Математическое ожидание постоянной величины равно самой постоянной: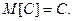

2. Постоянный множитель можно вынести за знак матема- тического ожидания:

3. Математическое ожидание алгебраической суммы слу –чайных величин равна алгебраической сумме их мате- матических ожиданий: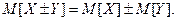

4. Математическое ожидание произведения независимых случайных величин равно произведению их математи -ческих ожиданий: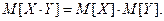

5. Математическое ожидание отклонения случайной вели- чины от её математического ожидания равно нулю:

3.2. Мода и медиана случайной величины.

Это ещё две характеристики положения случайной вели- чины.

Определение. Модой дискретной случайной величины называется её наиболее вероятное значение. Для непрерыв –ной случайной величины мода - это точка максимума функ- ции .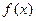

Если многоугольник распределения (для дискретной случай- ной величины) или кривая распределение (для непрерывной случайной величины) имеет две или более точек максимума, то распределение называется двухмодальным или многомо -дальным, соответственно.

Если нет ни одной точки максимума, то распределение называется антимодальным.

Определение. Медианой 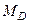случайной величины на – зывается такое её значение, относитеоьно которого равноверо- ятны получение большего или меньшего значения случайной величины, т.е.

Другими словами, - это абсцисса точки, в которой площадь под графиком плотности распределения (многоуголь- ником распределения) делится пополам.

Пример. Дана плотность случайной величины:

Найти медиану этой случайной величины.

Медиану 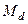найдём из условия . В нашем случае,

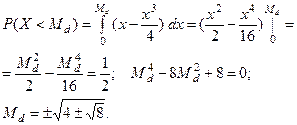
Из четырёх корней необходимо выбрать тот, который заключён между 0 и 2, т.е.

Замечание. Если распределение случайной величины одно- модальное и симметричное (нормальное), то все три характе -ристики положения: математическое ожидание, мода и медиа -на, совпадают.

3.3 Дисперсия и среднее квадратическое отклонение.

Значения наблюдаемых случайных величин, обычно, более или менее колеблются около некоторого среднего значения. Это явление называется рассеянием случайной величины око- ло её среднего значения. Числовые характеристики, показыва- ющие, насколько плотно сгруппированы возможные значения случайной велипины около среднего, называются характерис – тиками рассеяния. Из свойства 5 математического ожидания следует, что линейное отклонение значений случайной вели –чины от среднего значения не может служить характеристикой рассеяния, так как положительные и отрицательные отклоне –ния «гасят» друг друга. Поэтому основной характеристикой рассеяния случайной величины принято считать математичес - кое ожидание квадрата отклонения случайной величины от среднего.

Определение. Дисперсией называется математическое ожи –дание квадрата отклонения случайной величины от её матема- тического ожидания 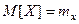(среднего значения), т.е.

(3)

Для дискретной случайной величины:

(4) для непрерывной случайной величины:

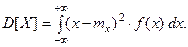(5)

Но, несмотря на удобства этой характеричтики рассеяния, желательно иметь характеристику рассеяния соразмерную с самой случайной величиной и её математическим ожиданием.

Поэтому вводится ещё одна характеристика рассеяния, кото -рая называется средним квадратическим отклонением и рав -на корню из дисперсии, т.е. .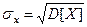

Для вычисления дисперсии удобно пользоваться формулой, которую даёт следующая теорема.

ТЕОРЕМА. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной вели -чины и квадратом её математического ожиданием, т.е.

В самом деле, по определению

Так как .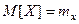

СВОЙСТВА ДИСПЕРСИИ:

1. Дисперсия постоянной случайной величины равна нулю, т.е.

2. Постоянный множитель сучайной величины выносится из дисперсии с квадратом, т.е.

3. Дисперсия алгебраической суммы двух случайных вели- чин равна сумме их дисперсий, т.е.

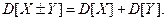
Следствие из 2 и 3 свойств:

Рассмотрим примеры..

Пример 1. Дан ряд распределения дискретной случайной величины. Найти её среднее квадратическое отклонение.

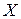
	- 1
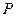
	0,2	0,05	0,2	0,3	0,25

Сначала найдём

Тогда среднее квадратическое отклонение

Пример 2. Пусть дана плотность распределения непрерыв -ной случайной величины:

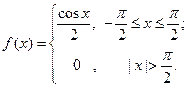
Найти её дисперсию и среднее квадратическое отклонение.

Тогда

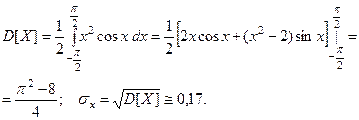
3.4 Моменты случайных величин.

Различают моменты двух видов: начальные и центральные.

Определение. Начальным моментом порядка 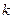случайной

величины называют математическое ожидание величины , т.е. .

Для дискретной случайной величины:

Для непрерывной случайной величины:

В частности, математическое ожидание - это началь- ный момент 1 – го порядка.

Определение. Центральным моментом полрядка 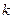слу -чайной величины 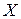называется математическое ожидание ве- личины , т.е.

Для дискретной случайной величины: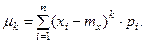

Для непрерывной -

Центральный момент 1 – го порядка равен нулю (свойство 5 математического ожидания); ; характеризует асимметрию (скощенность) графика плотности распределения. называется коэффициентом асимметрии.

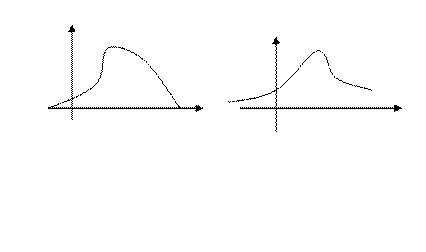
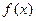
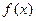
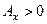
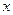
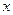
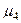служит для характеристики островерхости распределения.

Определение. Эксцессом случайной величины называет- ся число

Для номально распределённой случайной величины отноше- ние . Поэтому кривые распределения, более островер- хие, чем нормальная, имеют положительный эксцесс (), а более плосковерхие имеют отрицательный эксцесс ().

Пример. Пусть дана плотность распределения случайной величины :

Найти коэффициент асимметрии и эксцесс этой случайной величины.

Найдём необходимые для этого моменты:

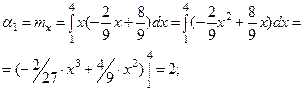
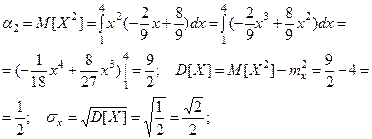
Тогда коэффициент асимметрии: (отрицательная асимметрия).

Эксцесс равен

Кроме рассмотренных выше начальных и центральных мо –ментов на практике иногда применяются так называемые абсо- лютные моменты.

Абсолютный начальный момент определяется формулой:

Абсолютный центральный момент задаётся формулой:

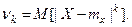
В частности, 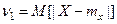называется средним ариф- метическим отклонением и иногда используется для харак -теристики рассеяния случайной величины.

Наряду с отмеченными выше числовыми характеристиками, для описания случайных величин используются понятия квантилей.

Определение. Квантилем уровня 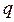(или 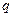- квантилем) называется такое значение случайной величины, при кото- ром функция её распределения принимает значение, равное 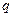, т.е.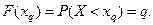

В обозначениях этого определения, медиана случайной ве- личины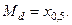

§ 4 ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

СЛУЧАЙНЫХ ВЕЛИЧИН

Сначала рассмотрим некоторые законы распределения дис- кретных случайных величин.

4.1 Биномиальное распределение.

Пусть случайная величина - это число появлений неко -торого события в серии из 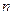независимых испытаний, в каждом из которых вероятность появления события 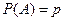, а вероятность не появления события 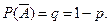Ряд распределения такой величины имеет вид:

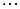
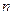
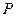
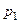
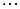
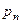
где 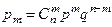. Такой ряд распределения называется биномиальным. Математическое ожидание случайной величины 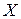в этом случае имеет вид:

(1)

Для вычисления этого выражения, продифференцировав по 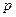следующее выражение: получим

Если мы умножим это равенство на 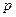, получим

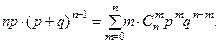(2)

Но 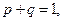а правые части равенств (1) и (2) совпадают, тогда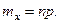

Продифференцировав то же самое выражение дважды, получим

Умножив полученное равенство на , получим:

Тогда

Таким образом,

Отсю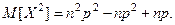да Тода

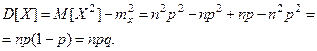
Итак, для биномиального распределения:

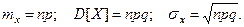
Пример. Произведено 20 независимых выстрелов по мише- ни. Вероятность попадания при каждом выстреле . Найти математическое ожидание, дисперсию и среднее квад -ратическое ожидание числа попаданий.

Случайная величина - число попаданий, распределена по биномиальному закону. Тогда

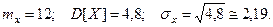
4.2 Распределение Пуассона.

Определение. Дискретная случайная величина 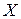имеет

закон распределения Пуассона, если она задаётся рядом рас- пределения

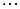
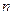
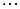
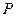
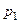
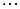
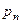
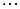
в котором вероятности определяются по формуле Пуассона

(3)

где 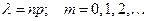( 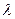- среднее число появлений события в серии испытаний, в каждом из которых вероятность появления события постоянная величина ).

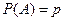Приведём без доказательства следующую теорему.

ТЕОРЕМА. Математическое ожидание и дисперсия случай -ной величины, распределённой по закону Пуассона, совпадают и равны параметру 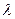этого закона, т.е.

При достаточно больших 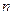(вообще при 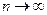) и малых значениях 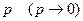при условии, что произведение 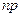- постоянная величина (), закон распределения Пуассона является хорошим приближением биномиального за –кона, т.е. распределение Пуассона - это асимптотическое рас -пространение биномиального закона. Иногда этот закон назы -вают законом редких явлений. По закону Пуассона распреде- лены, например, число сбоев автоматической линии, число от- казов системы в «нормальном режиме», число сбоев в работе АТС и т.п.

4.3 Геометрическое распределение.

Определение. Дискретная случайная величина име- ет геометрическое распределение, если 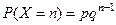, где для некоторого события ,

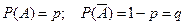и её ряд распределения имеет вид:

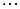
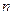
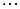
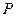
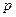
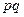
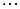
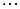
В этом случае вероятности представляют собой бесконечно убывающую геометрическую прогрессию и её сумма

.

ТЕОРЕМА. В случае случайной величины, имеющей геомет- рическое распределение с параметром 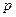, математическое ожидание и дисперсия вычисляются по формулам:

Пример. Производятся выстрелы по мишени до первого попа- дания. Вероятность попадания при каждом выстреле .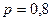

Составить ряд распределения случайной величины - «чис- ло попаданий». Найти её математическое ожидание и среднее квадратическое отклонение.

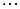
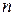
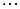
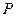
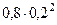
По теореме,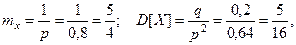

Дата добавления: 2014-11-29