
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Економетричні моделі з фіктивними змінними
|
|
|
|
Дослідження складних соціально-економічних явищ і процесів призводить до необхідності відображення в економетричних моделях дії як кількісних, так і якісних (атрибутивних) факторів. Безпосереднє уведення якісних за своєю сутністю факторних ознак у регресійні моделі неможливо здійснити, оскільки їх рівні набувають якісних, а не кількісних значень. У той же час атрибутивні факторні ознаки можуть істотно впливати на щільність зв’язку між пояснюваною і пояснювальними ознаками.
Скажімо, на рівень доходу працівника істотно впливає якісна змінна «освіта за фахом», а на вартість об’єкта нерухомості-такі якісні ознаки, як «наявність комунікацій», «тип будівлі», «кон'юнктура ринку» тощо. Подібні якісні ознаки вводять у регресійні моделі шляхом їх перетворення у фіктивні змінні, яким присвоюють певні дискретні кількісні значення.
У багатьох випадках якісні ознаки мають альтернативні (бінарні) рівні, яким відповідають булеві значення фіктивних змінних: «одиниця» - якщо ознака властива для об’єкта, який досліджується, «нуль» - у протилежному разі. Шляхом очевидного лінійного перетворення 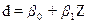 , де
, де 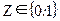 ;
;  - константи, якісній змінній (
- константи, якісній змінній ( ) можна присвоїти будь-які числові значення двох рівнів:
) можна присвоїти будь-які числові значення двох рівнів:  , якщо
, якщо 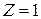 ;
; 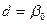 , якщо
, якщо  .
.
Фіктивні змінні, які набувають значень «1» або «0», називають dummy-змінними. У загальному випадку якісні ознаки можуть набувати значень декількох класів, а не лише бінарних. Це випливає із соціально-економічної сутності атрибутивних ознак. Для прикладу, «стать людини» як якісна змінна може набувати двох значень, а такі показники як «тип підприємства», «імідж виробника», «якість продукції», «рівень оподаткування», «політична стабільність» тощо – багатьох значень.
|
|
|
Варто відзначити, що з допомогою фіктивних змінних можна описати особливості сезонного виробництва і споживання продукції, а також регіональні (просторові) особливості соціально-економічних процесів.
Розмаїття видів багатофакторних регресійних моделей з фіктивними змінними зумовлюється структурою факторних (кількісних і/або якісних змінних) та результативних (кількісних або якісних змінних) ознак. Багатофакторна регресія може містити лише якісні зміні двох класів, тобто dummy-змінні, або змішану сукупність якісних і кількісних факторних ознак. У першому випадку отримаємо AOV-модель, у другому – ACOV-модель. Окрему групу становлять моделі із фіктивною залежною змінною – лінійні ймовірнісні моделі (LPM - моделі) та логістичні моделі з фіктивною змінною (Logist - моделі).
До числа основних завдань, які виникають при економетричному моделюванні складних соціально-економічних явищ і процесів з використанням якісних ознак, відносять обґрунтування кількості фіктивних змінних, оцінювання параметрів моделей з фіктивними змінними, перевірку значущості оцінок параметрів регресії, здійснення дисперсійного і коваріаційного аналізу.
До регресійної моделі може входити одна або декілька фіктивних змінних у поєднанні з кількісними факторними ознаками або без них. При цьому якісні змінні можуть набувати значень двох або більше класів.
Найпростішою моделлю є AOV -модель з однією фіктивною змінною (dummy-змінною), з допомогою якої описують якісні факторні ознаки, які набувають значень двох класів (категорій):
 , (4.105)
, (4.105)
де 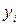 - залежна змінна;
- залежна змінна; 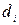 - dummy- змінна (
- dummy- змінна (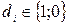 );
); 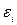 - випадкова величина;
- випадкова величина; 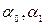 - параметри регресії.
- параметри регресії.
Якщо модель (4.105) описує залежність між середнім річним рівнем доходу на одну особу (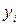 ) і рівнем освіти (
) і рівнем освіти (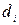 ), то значення dummy-змінної «одиниця», «нуль» відповідають респондентам двох категорій:
), то значення dummy-змінної «одиниця», «нуль» відповідають респондентам двох категорій: 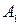 - особи з повною вищою освітою за фахом;
- особи з повною вищою освітою за фахом;  ;
;  - усі інші особи,
- усі інші особи, 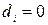 .
.
|
|
|
У такому разі середній річний дохід особи з повною вищою освітою за фахом буде становити 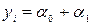 , а усіх інших осіб -
, а усіх інших осіб -  , а графіком функції (4.105) слугуватимуть дві паралельні до осі абсцис прямі лінії, які зміщені одна стосовно іншої на величину
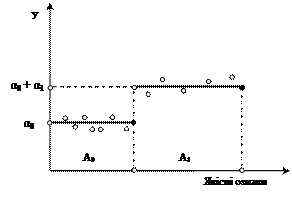
, а графіком функції (4.105) слугуватимуть дві паралельні до осі абсцис прямі лінії, які зміщені одна стосовно іншої на величину 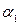 (рис. 4.5.а). Dummy-змінна відокремлює категорії осіб, а параметр
(рис. 4.5.а). Dummy-змінна відокремлює категорії осіб, а параметр  характеризує вплив освіти за фахом на середній рівень доходу.
характеризує вплив освіти за фахом на середній рівень доходу.

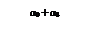
 | |||
 |
а) регресія з однією фіктивною б) регресія з двома фіктивними
зміною двох категорій змінними двох категорій
Рис. 4.4 Графічне представлення AOV -моделей
Ускладнимо модель (4.105) додатково включивши до неї нову якісну змінну двох категорій (стать-чоловіча, жіноча), що дасть змогу виявити вплив кожної із якісних ознак («освіта», «стать») на середній річний дохід особи. Загальна кількість якісних змінних буде дорівнювати чотирьом, однак у модель слід включати три dummy-змінні (на одиницю менше, ніж загальне можливе число якісних змінних). Для базової категорії dummy- змінна не уводиться з метою уникнення лінійної залежності між якісними змінними. У якості базової слід вибирати таку категорію, для якої значення результативної змінної  буде істотно меншим (більшим), ніж для усіх інших категорій. Наявність базової категорії дає змогу навести прозору економічну інтерпретацію параметрів регресії.
буде істотно меншим (більшим), ніж для усіх інших категорій. Наявність базової категорії дає змогу навести прозору економічну інтерпретацію параметрів регресії.
У нашому випадку у якості базової будемо розглядати категорію осіб жіночої статі без освіти ( ). Наступними будуть такі категорії:
). Наступними будуть такі категорії: 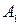 - категорія осіб жіночої статі з освітою (
- категорія осіб жіночої статі з освітою ( );
);  - категорія осіб чоловічої статі без освіти (
- категорія осіб чоловічої статі без освіти ( ).
).
Регресійна AOV -модель з dummy- змінними набере такого вигляду:
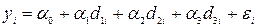 , (4.106)
, (4.106)
де 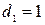 для осіб жіночої статі з освітою,
для осіб жіночої статі з освітою, 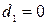 для усіх інших осіб;
для усіх інших осіб;  для осіб чоловічої статі без освіти,
для осіб чоловічої статі без освіти,  для усіх інших осіб;
для усіх інших осіб;  для осіб чоловічої статі з освітою,
для осіб чоловічої статі з освітою,  для усіх інших осіб.
для усіх інших осіб.
Параметр  характеризує середній річний дохід осіб базової категорії,
характеризує середній річний дохід осіб базової категорії,  - осіб категорії
- осіб категорії 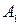 ,
,  - осіб категорії
- осіб категорії  . Числові значення параметрів
. Числові значення параметрів 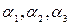 характеризують перевищення доходу осіб відповідної категорії стосовно осіб базової категорії.
характеризують перевищення доходу осіб відповідної категорії стосовно осіб базової категорії.
Геометричну інтерпретацію моделі (4.106) наведено на рис.4.4.б. Оцінювання параметрів AOV -моделей можна здійснити за даними відповідної вибірки скориставшись 1МНК з наступним тестуванням параметрів на статистичну значущість, а значить підтвердити, чи відхилити гіпотезу про істотність впливу якісних ознак на результативну.
|
|
|
Більш поширеними є ACOV- моделі, які містять у собі кількісні та якісні змінні. Перетворимо AOV -модель (4.105) до вигляду ACOV- моделі увівши додатково кількісну змінну (x) – «стаж праці»:
 (4.107)
(4.107)
де  - параметр, який характеризує вплив кількісної ознаки «стаж праці» на рівень доходу (
- параметр, який характеризує вплив кількісної ознаки «стаж праці» на рівень доходу ( );
); 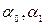 - характеристики математичного сподівання (
- характеристики математичного сподівання ( ) в залежності від значень якісної та кількісної ознак.
) в залежності від значень якісної та кількісної ознак.
Припускаючи, що  , отримаємо:
, отримаємо:
 , (4.108)
, (4.108)
 . (4.109)
. (4.109)
Геометрично модель (4.107) являє собою дві прямі лінії (4.108), (4.109), які паралельні між собою, мають однаковий нахил до осі ОХ ( ) і відрізняються диференційними коефіцієнтами перетину з віссю ОУ – (
) і відрізняються диференційними коефіцієнтами перетину з віссю ОУ – ( ) і (
) і (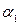 ) (рис. 4.5, а)). Диференційний перетин
) (рис. 4.5, а)). Диференційний перетин 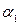 характеризує відмінність (зміщеність) перетину доходу осіб з повною вищою освітою за фахом (категорія
характеризує відмінність (зміщеність) перетину доходу осіб з повною вищою освітою за фахом (категорія 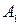 ) порівняно з базовою категорією
) порівняно з базовою категорією  .
.
Здійснивши аналітичні перетворення моделі (4.106) отримаємо її геометричну інтерпретацію, яку наведено на рис. 4.5, б).


а)  б)
б)
Рис. 4.5. Геометрична інтерпретація ACOV – моделей
Приклад 4.4. За даними статистичного щорічника України за 2007 рік (табл.4.13) про питому вагу середньомісячної заробітної плати жінок відносно чоловіків побудуємо AOV -модель виду  , де
, де 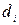 - фіктивна змінна, яка дорівнює нулеві для категорії «жінки» і одиниці для категорії «чоловіки»;
- фіктивна змінна, яка дорівнює нулеві для категорії «жінки» і одиниці для категорії «чоловіки»;  - відсоток заробітної плати.
- відсоток заробітної плати.
Таблиця 4.13
| Вид економічної діяльності | Відсотків до середньомісячної заробітної плати чоловіків |
| 1. Сільське господарство, мисливство, лісове господарство | 88,1 |
| 2. Промисловість | 67,3 |
| 3. Будівництво | 84,0 |
| 4. Торгівля | 78,3 |
| 5. Фінансова діяльність | 65,6 |
| 6. Операції з нерухомим майном, оренда, інжинірінг та надання послуг | 90,4 |
| 7. Державне управління | 80,5 |
| 8. Освіта | 84,1 |
| 9. Охорона здоров’я та надання соціальної допомоги | 85,2 |
| 10. Надання індивідуальних послуг; діяльність у сфері культури та послуг | 69,1 |
|
|
|
Економетрична модель має вигляд
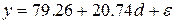 ,
, 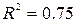
Високе значення коефіцієнта кореляції (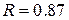 ) свідчить про щільність зв’язку, а розрахункове значення
) свідчить про щільність зв’язку, а розрахункове значення 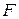 -критерію Фішера істотно перевищує критичне значення (
-критерію Фішера істотно перевищує критичне значення (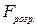 =24.0>5.32), що підтверджує адекватність моделі.
=24.0>5.32), що підтверджує адекватність моделі.
Параметр  характеризує відсоток середньої місячної заробітної плати жінок відносно заробітної плати чоловіків у середньому для всіх видів економічної діяльності в Україні, а значення параметра
характеризує відсоток середньої місячної заробітної плати жінок відносно заробітної плати чоловіків у середньому для всіх видів економічної діяльності в Україні, а значення параметра  характеризує відносне перевищення заробітної плати чоловіків стосовно жінок. Статистична значущість параметрів моделі підтверджується за критерієм Стьюдента.
характеризує відносне перевищення заробітної плати чоловіків стосовно жінок. Статистична значущість параметрів моделі підтверджується за критерієм Стьюдента.
Економетричні моделі з фіктивними змінними є ефективним засобом дослідження сезонних економічних явищ і процесів. Можна навести ряд процесів, які підпорядковані сезонним коливанням, зокрема, зайнятість у сільському господарстві, попит на окремі групи товарів, виконання монтажно-будівельних робіт, пропозиція і попит на валюту, формування цін на продовольчі товари, надання туристичних послуг тощо. Виокремлення сезонних збурень для ряду динаміки дає змогу дослідити істотність впливу сезонних коливань у певних часових періодах, а також виявити основну тенденцію. Щодо тривалості періоду часу, то при дослідженні макроекономічних процесів доцільно у якості часової одиниці вибирати рік, а при аналізі показників економічного зростання суб’єктів господарювання – квартал або місяць.
Поширеним прикладом економетричних моделей з фіктивними змінними, за допомогою яких описують сезонний характер споживання певного товару (пиво, морозиво, спортивний інвентар, туристичні послуги тощо), є моделі такого вигляду:
 (4.110)
(4.110)
 (4.111)
(4.111)
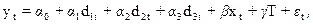 (4.112)
(4.112)
де 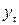 - обсяг споживання товару;
- обсяг споживання товару;  - dummy-змінні, які набувають значення «одиниця» для відповідного кварталу
- dummy-змінні, які набувають значення «одиниця» для відповідного кварталу  і «нуль» для усіх інших кварталів (базовим вважаємо четвертий);
і «нуль» для усіх інших кварталів (базовим вважаємо четвертий); 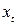 - рівень доходу споживача;
- рівень доходу споживача;  - індекс кварталу (
- індекс кварталу (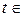
 );
);  - порядковий номер року.
- порядковий номер року.
Слід відзначити, що наведені моделі містять три фіктивні змінні. Параметри 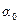 , (
, ( ), (
), ( ),(
),(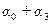 ) характеризують міру впливу сезонних коливань на споживання товару у базовому четвертому, першому, другому і третьому кварталах відповідно, а параметри
) характеризують міру впливу сезонних коливань на споживання товару у базовому четвертому, першому, другому і третьому кварталах відповідно, а параметри  - обсяги додаткового споживання продукту у відповідному кварталі стосовно базового.
- обсяги додаткового споживання продукту у відповідному кварталі стосовно базового.
Параметр 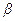 характеризує схильність до споживання, тобто вказує на частку доходу, яка скеровується на споживання товару, а параметр
характеризує схильність до споживання, тобто вказує на частку доходу, яка скеровується на споживання товару, а параметр 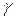 -часову тенденцію до споживання товару по роках.
-часову тенденцію до споживання товару по роках.
Модель вигляду (4.110) дає змогу виявити сезонні коливання процесу споживання певного товару, (4.111) – встановити тренд, а (4.112) об’єднує обидві попередні моделі.
Приклад 4.5. За даними про обсяги валового доходу будівельного підприємства, а також витратами на виконання будівельно-монтажних робіт, виявимо вплив сезонних коливань на валовий дохід підприємства.
Таблиця 4.14
| Рік, Т | Квартал, t | Валовий дохід, тис. грн., yt | Операційні витрати, тис. грн., xt | Dummy - змінні | ||
| d2 | d3 | d4 | ||||
Побудуємо AOV – модель з метою виявлення впливу сезонних коливань на валовий дохід підприємства. У якості базової категорії виберемо ознаку першого кварталу.
Шукана економетрична модель має вигляд:

де 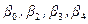 - параметри моделі;
- параметри моделі;  - випадкова величина;
- випадкова величина; 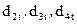 - dummy – змінні кожна з яких набуває значень «нуль» або «одиниця»;
- dummy – змінні кожна з яких набуває значень «нуль» або «одиниця»;  - ознака кварталу.
- ознака кварталу.
За розрахунками числова модель набере такого вигляду:


Адекватність моделі за 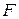 - критерієм Фішера підтверджується, усі параметри є статистично значущими за
- критерієм Фішера підтверджується, усі параметри є статистично значущими за  - критерієм Стьюдента. Значення параметрів
- критерієм Стьюдента. Значення параметрів 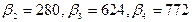 характеризують розмір перевищення валового доходу у відповідному кварталі стосовно доходу у базовому першому кварталі (
характеризують розмір перевищення валового доходу у відповідному кварталі стосовно доходу у базовому першому кварталі (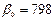 ).
).
З урахуванням даних щодо обсягів операційних витрат 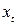 перетворимо початкову AOV -модель до вигляду ACOV -моделі:
перетворимо початкову AOV -модель до вигляду ACOV -моделі:

За розрахунками отримаємо
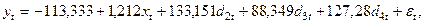

Модель адекватна за F – критерієм Фішера, кожний параметр моделі є статистично значущим. Відзначимо закономірну істотність впливу обсягів витрат 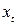 на валовий дохід підприємства – з кожної одиниці операційних витрат підприємство отримує 1,212 одиниць доходу. Від’ємне значення параметра
на валовий дохід підприємства – з кожної одиниці операційних витрат підприємство отримує 1,212 одиниць доходу. Від’ємне значення параметра  =-113,333 можна тлумачити як індикатор можливості виникнення збитків підприємства у разі відсутності витрат на матеріали, комплектуючі та на оплату праці персоналу у першому і третьому кварталах.
=-113,333 можна тлумачити як індикатор можливості виникнення збитків підприємства у разі відсутності витрат на матеріали, комплектуючі та на оплату праці персоналу у першому і третьому кварталах.
З метою виявлення річного тренду щодо приросту валового доходу підприємства перетворимо модель до такого вигляду:
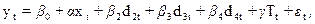
де Т – ознака року (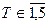 ).
).
За розрахунками отримаємо:
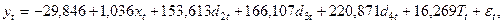

Модель адекватна за 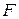 - критерієм Фішера, усі параметри за винятком
- критерієм Фішера, усі параметри за винятком 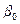 і
і 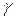 є статистично значущими за
є статистично значущими за  - критерієм.
- критерієм.
Значення 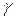 =16,269 можна тлумачити як розмір квартального приросту у кожному році обсягу валового доходу підприємства стосовно попереднього року.
=16,269 можна тлумачити як розмір квартального приросту у кожному році обсягу валового доходу підприємства стосовно попереднього року.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 4677; Нарушение авторских прав?; Мы поможем в написании вашей работы!