Системи одночасних рівнянь

Економетричні моделі, розглянуті у попередніх параграфах даного розділу, складалися з одного рівняння і описували односторонній зв'язок між залежною змінною 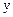і незалежними змінними 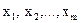. Економетричні дослідження у ряді випадків призводять до необхідності побудови моделей, які представляються системою рівнянь. Такі моделі характеризують процеси, що відбуваються одночасно, тому сукупність взаємопов’язаних між собою рівнянь називають системою одночасних (симультативних) рівнянь.

Взаємозв’язки між змінними, які входять до складу економетричної моделі, поданої у вигляді системи одночасних рівнянь, можуть бути як стохастичними, так і детермінованими. У першому випадку вони описуються за допомогою регресійних рівнянь, а у другому – за допомогою тотожностей (балансових взаємозв’язків між змінними моделі).

У практичних дослідженнях, як правило, користуються системою лінійних рівнянь, а нелінійність зв’язків апроксимується лінійними співвідношеннями.

Рівняння, які описують динаміку окремих показників моделі, виражаються за допомогою лагових змінних (часових лагів).

Приклад економетричної моделі, записної у вигляді системи симультативних рівнянь, наведено у 1-му розділі посібника (модель Дж.Кейнса). Іншим класичним прикладом може слугувати модель одночасного формування попиту і пропозиції на товар у залежності від ціни:

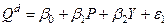; (4.113)

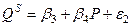, (4.114)

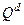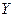де - обсяг попиту; - обсяг пропозиції; - дохід; 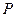- ціна.

Якщо вважати, що ринок перебуває у стані рівноваги, то слід додатково накласти умову (4.115):

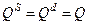. (4.115)

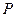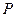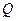Тоді ціна рівноваги формується одночасно із попитом і пропозицією, величини і вважаються пояснюваними змінними, а дохід 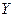- пояснювальною змінною.

Змінні, які входять до складу одночасних рівнянь, прийнято поділяти на екзогенні та ендогенні. Екзогенні змінні вважаються наперед заданими, тобто їх значення формуються поза моделлю. Змінні, значення яких обчислюються в результаті реалізації моделі і визначаються на основі внутрішньої структури економічної системи, називаються ендогенними змінними. Для розглянутої вище моделі змінн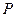і і 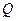є ендогенними, а змінна 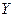- екзогенною.

Якщо розглядати екзогенні та ендогенні змінні з математичної точки зору, то основна відмінність між ними полягає у тому, що екзогенні змінні не корелюють з помилками регресії, а ендогенні можуть корелювати. Існування взаємозалежності (прямих і зворотних зв’язків) між економічними показниками є порушенням класичного припущення 4 про відсутність кореляції між пояснювальними змінними і випадковими величинами. Не вдаючись до строгих математичних викладень відзначимо, що застосування 1МНК у випадку корелювання пояснювальних змінних з випадковими величинами призводить до отримання зміщених оцінок (оцінок з відхиленнями) моделі.

У загальному випадку економетричну модель, яка представлена за допомогою системи одночасних рівнянь, можна записати так:

,

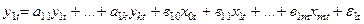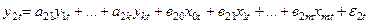, (4.116)

.

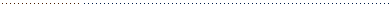
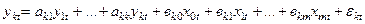Змінна 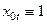і використовується для множення на вільні члени рівнянь системи. Якщо деяка змінна не входить до рівняння, то відповідний їй коефіцієнт рівний 0. Якщо -те рівняння є тотожністю, то .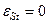

Так як рівняння (4.116) виражають ендогенні змінні як функції від екзогенних (попередньо визначених) змінних, інших ендогенних змінних та випадкових величин, тобто безпосередньо відображають структуру зв’язків між змінними, то таке представлення називають структурною формою економетричної моделі.

Система (4.116) у матричній формі приймає вигляд:

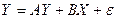, (4.117)

де 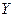- вектор ендогенних змінних; 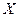- матриця екзогенних змінних; 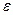- вектор залишків; 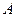- матриця коефіцієнтів при ендогенних змінних; 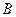- матриця коефіцієнтів при екзогенних змінних.

Розв’яжемо (4.117) відносно :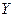

,

,

.

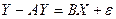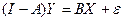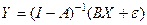Якщо позначити 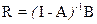, то отримаємо

(4.118)

або

,

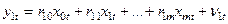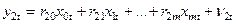, (4.119)

,

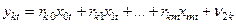де 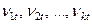- лінійна комбінація залишків .

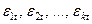Економетричну модель, яка представлена системою (4.119), називають зведеною (скороченою) моделлю.

На основі зведеної форми можна отримати значення ендогенних змінних, але рівняння зведеної форми пояснюють ці значення тільки через екзогенні змінні і не показують взаємозв’язку між залежними змінними. Інакше кажучи, зведена форма дає значно менший рівень деталізації взаємозв’язків між змінними, ніж структурна.

Для знаходження оцінок коефіцієнтів зведеної форми можна скористатися 1МНК. Після цього може виникнути задача визначення параметрів структурної форми на основі отриманих оцінок зведеної форми, вирішення якої пов’язується із проблемою ідентифікації моделі – проблемою однозначної відповідності між зведеною і структурною формами.

Модель називається ідентифікованою, якщо жодна лінійна комбінація рівнянь структурної форми не забезпечує отримання рівняння, до якого входять ті ж змінні, що й до певного рівняння структурної форми. Якщо модель є ідентифікованою, то зведена форми визначається однозначно за допомогою (4.119), причому матриця 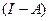ніколи не буває виродженою.

Необхідною умовою ідентифікації вважається виконання для кожного рівняння моделі (4.116) умови:

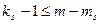, (4.120)

де -кількість ендогенних змінних в 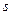-му рівнянні структурної форми; 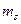- кількість екзогенних змінних в 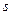-му рівнянні структурної форми; 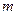- загальна кількість екзогенних змінних, які включені до моделі.

Якщо для всіх рівнянь структурної форми умова (4.120) виконується як строга рівність, то система рівнянь є точно ідентифікованою.

Якщо для якого-небудь рівняння структурної форми умова (4.120) виконується як нерівність, то рівняння вважається надідентифікованим.

Якщо для яког-небудь рівняння структурної форми умова (4.120) не виконується, то система рівнянь вважається неідентифікованою. Неідентифікованість системи рівнянь, як правило, змушує дослідника переглянути специфікацію моделі.

Умова (4.120) є лише необхідною (обов’язковою) умовою ототожнення. Попередньо визначені змінні, які опущені в окремому рівнянні, але присутні в моделі, можуть виявитися залежними. Тому навіть при виконанні умови (4.120) оцінити структурні параметри на основі коефіцієнтів скороченої форми не вдається.

Достатня умова точної ідентифікації виконується тоді, коли визначник матриці, складеної із коефіцієнтів при змінних, які відсутні у досліджуваному рівнянні, відмінний від нуля, а її ранг не менший за .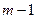

За умови точної ідентифікації кожного структурного рівняння параметри економетричної моделі можна оцінити за допомогою непрямого методу найменших квадратів (НМНК), алгоритм якого полягає у виконанні таких кроків:

• складається зведена форма економетричної моделі і за допомогою 1МНК оцінюються параметри кожного з рівнянь зведеної форми;

• за допомогою алгебраїчних перетворень переходять від зведеної форми до структурних рівнянь і на основі оцінених параметрів зведеної форми знаходять числові оцінки структурних параметрів.

Доведено, що отримані за допомогою НМНК оцінки параметрів структурної форми є зміщеними в бік заниження. Із збільшенням чисельності вибірки відхилення зменшуються.

Якщо система одночасних рівнянь є надідентифікованою, то застосувати НМНК не можна. Для оцінювання параметрів таких моделей розроблені спеціальні методи, одним з яких є двокроковий метод найменших квадратів (2НМК). Алгоритм реалізації 2НМК полягає у виконанні таких процедур:

• складається зведена форма моделі і за допомогою 1МНК знаходять оцінки параметрів кожного її рівняння;

• на основі побудованих на першому кроці рівнянь зведеної форми знаходять розрахункові значення ендогенних змінних, які розташовані у правій частині структурного рівняння;

• за допомогою 1МНК знаходять оцінки параметрів кожного структурного рівняння, використовуючи в якості вхідних даних фактичні значення попередньо визначених змінних і розрахункові значення ендогенних змінних, які містяться у правій частині даного структурного рівняння.

Метод 2НМК можна застосувати і для знаходження оцінок параметрів точно ідентифікованих рівнянь (у цьому випадку НМНК і 2МНК забезпечать ідентичні оцінки).

Економетричні моделі деяких процесів можна записати у вигляді такої системи рівнянь:

,

,

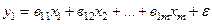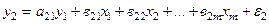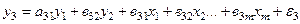, (4.121)

.

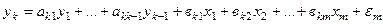Модель (4.121) називають рекурсивною системою рівнянь (рекурсивною моделлю). Оцінювання параметрів кожного рівняння можна виконати за допомогою 1МНК. На основі значень пояснювальних змінних спочатку знаходять оцінене значення першої ендогенної змінної . Обчислене (теоретичне) значення 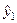використовується як пояснювальна змінна у другому рівнянні. Для оцінювання параметрів другого рівняння можна знову використати 1МНК, так як всі змінні у правій частині рівняння незалежні від залишку 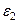( 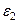і 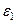є незалежними, тому і 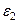є також незалежними). Аналогічним чином оцінюють параметри наступних рівнянь.

Точковий прогноз ендогенних змінних отримують шляхом підстановки значень екзогенних змінних у зведену форму рівнянь:

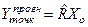, (4.122)

де 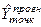- вектор прогнозних значень ендогенних змінних;

- вектор прогнозних значень екзогенних змінних;

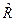- матриця оцінок коефіцієнтів рівнянь регресії зведеної форми.

Довірчі інтервали прогнозного значення для 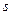-ої ендогенної змінної визначаються згідно співвідношення:

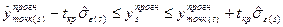, (4.123)

де 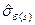- оцінка середнього квадратичного відхилення залишків 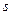-го рівняння зведеної форми.

Приклад 4.6. На основі даних спостережень, поданих у табл. 4.15, подувати економетричну модель у вигляді системи одночасних структурних рівнянь та оцінити її параметри

Таблиця 4.15

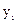
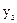
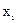
Номер спостереження	Споживання продукції, гр.од.	Ціна одиниці продукції, гр.од.	Дохід, гр.од.	Витрати на вироництво одиниці продукції, гр.од.
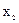
		3,53		2,54
		3,38		2,56
		3,61		2,76
		3,34		2,32
		3,72		2,66
		3,02		2,19
		3,55		2,39
		2,92		2,02
		3,62		2,64
		2,89		2,06

При побудові економетричної моделі будемо вважати, що попит (обсяг споживання) лінійно залежить від ціни та доходу, а ціна – від попиту і витрат. Тоді модель можна представити за допомогою таких структурних рівнянь:

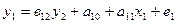- попит,

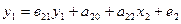- ціна.

Економетрична модель у зведеній формі має вигляд:

,

.

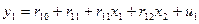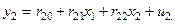Так як ціна і попит (споживання) формуються одночасно, то модель містить дві ендогенні змінні (у_{1 і} у₂) і дві екзогенні змінні (х₁, х₂). Для перевірки моделі на ідентифікованість скористаємося умовою (4.120).

Для обох рівнянь ця умова виконується як строга рівність (2-1=2-1), тому рівняння є точно ідентифікованими. Отже, оцінювання невідомих параметрів економетричної моделі можна виконати за допомогою НМНК. Застосовуємо 1МНК і знаходимо оцінки рівнянь регресії зведеної форми моделі:

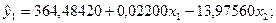
(3,48) (4,52) (-0,60)

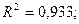
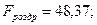
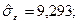
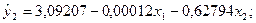
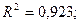
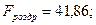
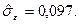
У дужках подано розрахункові значення t – критеріїв для перевірки значущості коефіцієнтів рівняння регресії. З таблиць розподілу для 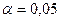знаходимо, що t_кр=2,37 і F_кр=4,74. Можна зробити такі висновок:

• рівняння економетричної моделі є адекватними;

• у рівнянні попиту статистично незначущою є змінна х₂, а у рівнянні ціни – змінна х₁.

Друге рівняння зведеної форми розв’язуємо відносно х₂ і підставляємо отриманий вираз у перше рівняння зведеної форми. В результаті отримуємо перше рівняння структурної форми:

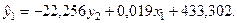
Аналогічно, розв’язавши перше рівняння зведеної форми, знаходимо таке рівняння структурної форми:

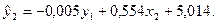
Оцінювання параметрів розглянутої вище моделі можна виконати також за допомогою 2 МНК.

З цією метою на основі побудованих регресійних рівнянь зведеної форми розраховуємо теоретичні значення ендогенних змінних 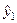і (табл.4.16).

Таблиця 4.16

Номер спостереження			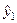Номер спостереження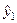
	544,1589	3,5525		580,3298	3,1678
	573,4430	3,4092		533,2062	3,4216
	545,5936	3,6669		605,0764	2, 9431
	589,7533	3,1901		540,7596	3,6258
	526,7541	3,7108		618,9252	2,8922

Використовуючи в якості вхідних даних фактичні значення екзогенних змінних і теоретичні значення ендогенних змінних за допомогою 1МНК знаходимо оцінки параметрів кожного структурного рівняння. Отримуємо таку структурну форму моделі:

;

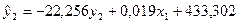(-0,60) (2,20) (1,99)

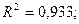
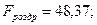
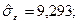
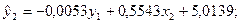
(-2,28) (2,04) (2,61)

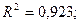
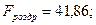
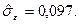
Результати моделювання, отримані за допомогою НМНК і 1МНК, співпадають.

Оцінки коефіцєінтів регресії є статистично незначущими. Для того, щоб отримати статистично значущі результати, необхідно змінити специфікацію моделі або збільшити кількість спостережень.

Дата добавления: 2014-12-16