Показательная функция, гиперболические функции

Показательные и логарифмические выражения

СПРАВОЧНЫЕ ТАБЛИЦЫ

7.1. Основные физические постоянные (округленные значения)

Физическая постоянная	Обозначения	Значение
Ускорение свободного падения Гравитационная постоянная Число Авогадро Универсальная газовая постоянная Постоянная Больцмана Скорость света в вакууме	g g NA R k c	9,81 м/с^2 6,67 10^-11 м^3/(кг∙ с^2) 6,02 I0^23 моль ^-1 8,31 Дж/(моль K) 1,38×I0^-23 Дж/К 3×10^8 м/с

7.2. Некоторые астрономические величины

Наименование	Значение
Радиус Земли Mасса Земли Радиус Солнца Масса Солнца Радиус Луны Масса Луны Расстояние от центра Земли до центра Солнца Расстояние от центра Земли до центра Луны	6,37×10^6 м 5,98×I0^24 кг 6,95×10^8 м 1,98×10^30 кг 1,74×10^6 м 7,33×10 ^22 кг   1, 49×10^11 м   3,84×10^8 м

7.3. Свойства некоторых твердых тел

Вещество	Плотность, 10^3 кг/м^3	Температура плавления ^0С	Удельная теплоемкость Дж/(кг×К)	Удельная теплота плавления, 10^5 Дж/кг
Алюминий Железо Латунь Лед Медь Олово Платина Пробка Свинец Сталь Цинк Серебро	2,6 7,9 8,4 0,9 8,6 7,2 21,4 0,2 11,3 7,7 7,0 10,5	-		3,22 2,72 - 3,35 1,76 0,586 1,13 - 0,226 - 1,17 0,88

7.4. Удельная теплота испарения воды при разных температурах

t, ^oC
r, 10^5 Дж/кг	24,9	23,8	22,6	19,4

7.5. Свойства некоторых жидкостей

Жидкость	Плотность, кг/м^3	Удельная теплоемкость при 20^0 С, Дж/(кг×К)
Бензол Вода Глицерин Касторовое масло Керосин Ртуть Спирт	0,88 1,00 1,20 0,9 0,8 13,6 0,9

7.6. Относительные атомные массы

А и порядковые номера Z некоторых элементов

Элемент	Сим-вол	А	Z	Элемент	Сим-вол	А	Z
Азот	N			Медь	Cu
Алюминий	Al			Молибден	Mo
Аргон	Ar			Натрий	Na
Водород	H			Неон	Ne
Вольфрам	W			Никель	Ni
Гелий	He			Олово	Sn
Железо	Fe			Платина	Pt
Золото	Au			Ртуть	Hg
Калий	K			Сера	S
Кальций	Ca			Серебро	Ag
Кислород	O			Уран	U
Магний	Mg			Углерод	C
Марганец	Mn			Хлор	Cl

7.7. Множители и приставки для образования

десятичных кратных и дольних единиц иих наименования

Приставка		Приставка
наимено-вание	обозна-чение	множи-тель	наимено-вание	обозна-чение	множи-тель
экса	Э	10^18	деци	Д	10^-1
пэта	П	I0^15	санти	с	10^-2
тера	Т	10^12	милли	м	10^-3
гига	Г	I0^9	микро	мк	10^-6
мега	М	10^6	нано	н	10^-9
кило	к	10^3	пико	п	10^-12
гекто	г	10^2	фемто	ф	10^-15
дека	да	10^1	атто	а	10^-18

Показательной функцией называется функция

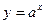, где .

Основные свойства показательной функции.

1. Область определения: .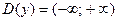

2. Множество значений: .

3. Четность и нечетность: не обладает свойством четности.

4. Периодичность: не периодическая.

5. Нули функции: нулей не имеет.

6. Промежутки знакопостоянства:функция положительна для .

7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания: если функция возрастает для всех ; если – убывает для .

9. Точки пересечения с осями координат: пересекает ось Оу в точке , ось не пересекает.

10. Асимптоты: прямая y = 0 (ось ) является горизонтальной асимптотой.

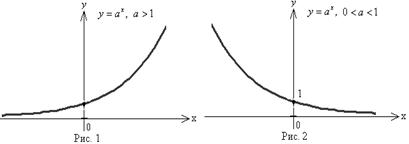
11. График функции для a > 1 изображен на рисунке 1, для – на рис. 2.

Из свойств функции следует: неравенство 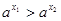равносильно неравенству:

1) 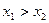, если ,

2) 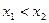, если .

Показательная функция с основанием , где иррациональное число , называется экспонентой, пишут 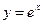или .

Через показательные выражения с основанием определяются гиперболические функции.

Гиперболическим синусом называется функция

.

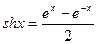Дата добавления: 2014-12-16