Волновая функция. Гармоническая волна. Параметры гармонической волны

Математически, процесс распространения волны вдоль некоторой оси х описывается так называемой волновой функцией видаx =f (x-ut), где f – любая функция аргумента x–ut (на практике, впрочем, ее значения не могут быть бесконечными). Линия, вдоль которой распространяются волна (в однородных средах это прямая линия) называется лучом. В нашем примере лучом является ось х. Параметр u называется фазовой скоростью волны. Если распространяющееся колебание – гармоническое, т.е. в каждой точке пространства происходит по закону синуса (косинуса), то для волновой функции бегущей волны имеем

x(x, t)= А sin(kx –w t –a), (8.2.1)

где w - частота колебаний, a - некоторая константа (начальная фаза), а через k обозначена величина w / u. Параметр k называется волновым числом. Как видно из (8.2.1), и временная и пространственная зависимость гармонической волны – синусоиды. Если в (8.2.1) зафиксировать t, то зависимость волновой функции от х дает как бы моментальную фотографию волны (застывшую синусоиду). Пространственный период ее, т.е. расстояние между точками, в которых совпадает значение x и значение ее производной по координате, называется длиной волны и обозначается обычно буквой l (рис. 8.2.1). График x(х) похож на график гармонического колебания, однако, отличается по существу. Для упругой волны он дает зависимость плотности (т.е. картину сгущений и разрежений среды) от координаты х. График колебаний, например, в точке В с координатой х дает зависимость плотности среды в этой точке от времени. Картину распространения волны можно представить, если застывшую синусоиду на рис. 8.2.1 привести в движение вдоль оси х со скоростью u. Две последовательных 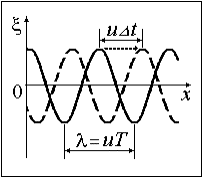“моментальных фотографии” волны в моменты времени t и t+ D t показаны на рис. 8.2.2. Точка волны с определенной фазой, например, точка максимума x на рис. 8.2.2, смещается за это время на расстояние u D t. Легко видеть, что l= u T =2p/ k.

Геометрическое место точек, до которых доходят колебания к данному моменту времени t называется волновым фронтом. Геометрическое место точек, находящихся в одинаковой фазе колебания, называется волновой поверхностью. Волновая поверхность, на которой колебание находится в максимальной фазе, называется гребнем волны. Гребни, как и все волновые поверхности, движутся со скоростью u (см. рис. 8.2.2).

Как можно проверить непосредственной подстановкой выражения (8.2.1), гармоническая волновая функция подчиняется уравнению

, (8.2.2)

Это уравнение – частный случай общего волнового уравнения для так называемых линейных сред. В таких средах малое изменение внешней силы, приложенной к малому объему среды, вызывает пропорциональную этому изменению деформацию объема. Для таких сред уравнение вида (8.2.2) выводится из второго закона Ньютона. При этом значение скорости u определяется через параметры среды, в частности, через плотность среды r и коэффициенты, характеризующие упругость. Например: для продольных волн в твердом тонком стержне (E – модуль Юнга материала стержня), для поперечных волн в твердом теле 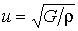(G – модуль сдвига), для поперечных волн в струне (F – сила натяжения струны, S – площадь ее сечения). Для звуковых волн в газе (g – коэффициент Пуассона, p давление газа).

Дата добавления: 2014-12-16