Кривые безразличия. Пусть для простоты в набор входят только два товара Х и У

Пусть для простоты в набор входят только два товара Х и У. Изобразим на двухмерной плоскости пространство наборов товаров. Каждая точка будет соответствовать набору, содержащему какое-то количество товаров Х и У.

Эта точка разобьет пространство благ на четыре квадранта.

Руководствуясь принципом: больше - значит лучше, назовем правый-верхний участок местом наборов, лучших по сравнению с А, т.е. более предпочтительных. Аналогично, левый-нижний участок – это место наборов, менее предпочтительных по сравнению с А, потому что в них меньше и товара Х и товара У. Значит, если существуют такие же по полезности наборы, то они будут лежать в правом-нижнем и левом-верхнем квадрантах.

Соединим все точки, соответствующие наборам благ, имеющих одинаковую полезность для потребителя. Назовём полученную линию кривой безразличия. Каждая кривая безразличия графически отображает множество наборов благ, обладающих одинаковой полезностью для потребителя.

Кривые безразличия обладают рядом свойств:

- они не пересекаются;

- они выпуклы к началу координат и имеют отрицательный наклон;

- чем дальше от начала координат расположена кривая, тем более высокому уровню полезности она соответствует;

- через любую точку на плоскости двух благ можно провести кривую безразличия; и таких кривых будет бесконечно много.

Множество кривых безразличия, каждая из которых представляет различный уровень полезности, составляет карту кривых безразличия.

Допустим, потребитель оценивает различные наборы из двух благ, одно из которых – еда, а другое – одежда. И считает, что они для него равноценны.

Набор благ	Количество еды	Количество одежды
А
Б

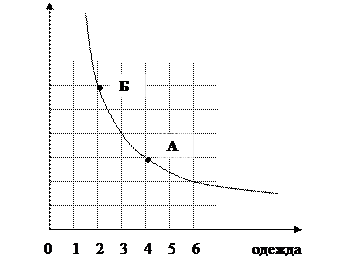
Набор А, содержащий 3 единицы еды и 4 единицы одежды, приносит потребителю такую же полезность, что и набор Б, содержащий 6 единиц еды и 2 единицы одежды, если наборы А и Бравноценны для данного потребителя, и, значит, на графике точки, обозначающие эти два набора, принадлежат одной кривой безразличия U₁.

Теперь рассмотрим не два, а четыре набора благ. Продолжим таблицу:

Набор благ	Количество еды	Количество одежды
А
Б
В
Г

Рассмотрим набор благ В, содержащий 6 единиц еды и 4 единицы одежды. Для потребителя набор В предпочтительнее, чем набор А, так как он содержит одежды столько же, а еды на 3 единицы больше. Также набор В предпочтительнее, чем набор Б, так как содержит еды столько же, а одежды на 2 единицы больше. Следовательно, набор В лежит на более высокой кривой безразличия U₂, так как обеспечивает потребителю более высокий уровень полезности.

Если мы рассмотрим набор Г и будем рассуждать аналогичным образом, то придём к выводу, что наборы А, Б и В предпочтительнее, чем набор Г. Набор Г лежит на более низкой кривой безразличия U₀.

Еще одно важное понятие ординалистской теории – предельная норма замещения благ(marginal rate of substitution – MRS).

Норма замещения двух благ показывает, сколько единиц одного блага потребитель готов обменять на одну единицу другого блага, сохраняя при этом уровень полезности неизменным.

RS_XY = - ΔY/ΔX, где Y – количество одного блага, Х – количество другого блага.

Поскольку Х и Y изменяются в разных направлениях (количество Х растет, а количество Y сокращается ), то поставив знак «минус», мы норму замещения делаем положительной величиной.

Пусть в новогоднем подарке (потребительской корзине) только два вида благ – мандарины (М) и пряники (П). Все подарки приносят одинаковое удовольствие, т.е. наборы благ приносят потребителю одинаковую полезность, а значит, лежат на одной кривой безразличия. Рассмотрим подарки А и Б.

Набор А содержит 12 мандаринов и 1 пряник. Набор Б содержит 6 мандаринов и 2 пряника. Переходя от набора А к набору Б, потребитель отказывается от 6 мандаринов, чтобы получить 1 дополнительный пряник.

В данном случае RS _пм = -(-6/1) = 6.

При переходе от набора Б к набору В, потребитель отказывается от двух мандаринов ради одного дополнительного пряника. RS _пм = -(-2/1) =2.

При переходе от набора В к набору Г потребитель отказывается только от одного мандарина ради одного дополнительного пряника. RS _пм = -(-1/1) =1.

Заметим, что чем больше мандаринов и меньше пряников оказалось в наборе, тем больше готовность отказаться от мандаринов ради пряника. Аналогично и в другую сторону – чем большим количеством пряников человек располагает, тем меньшим количеством мандаринов он готов пожертвовать, чтобы получить больше пряников. Из примера видно, что при движении вдоль выпуклой кривой безразличия от набора А к набору Г, норма замещения мандаринов пряниками убывает.

Если товары являются бесконечно делимыми, то ΔХ можно будет уменьшать, приближая друг к другу точки на кривой безразличия, и тогда можно получить предельную норму замещения.

MRS_xy = lim ().

Говоря о предельных величинах, считаем, что величина Х изменилась чуть-чуть. Это правильно и дает интуитивное представление о процессе. Речь идёт о производной, но этот факт в школьном курсе не используется.

Предельная норма замещения равна тангенсу наклона касательной, проведенной к кривой безразличия в данной точке (берём со знаком плюс для сохранения экономического смысла).

Задача 8.

Петя считает, что ему одинаково полезно еженедельно выпивать как 8 стаканов молока и 3 стакана кефира, так и 6 стаканов молока и 4 стакана кефира. Чему в данном случае равна его норма замены кефира на молоко?

Дата добавления: 2014-12-16