Равновесие потребителя

Решение.

Решение.

Определим, какая прямая соответствует заданному бюджетному ограничению.

I₁ = 60, P_Х = 10, P_Y = 15.

Х_макс = 6, У_макс = 4, следовательно, это прямая, расположенная на рисунке ниже.

Поскольку бюджетное ограничение изменило угол наклона, значит, изменилось соотношение цен 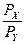. Так как изменился лишь один фактор, то размер бюджета остался неизменным (60д.е.) Максимальное количество Х в обоих случаях равно 6. Это значит, что Р_х не изменилась. Очевидно, что изменилась цена на товар Y. Максимальное количество У увеличилось с 4 до 6, значит, цена товара У уменьшилась. Найдем новую цену Y: 60:6 = 10. Запишем новое бюджетное ограничение: 10∙ Х + 10∙ Y = 60.

Ответ: P_Y уменьшилась; 10 Х + 10 Y = 60.

Задача 14.

Цены на товары Х и У выросли в 2 раза. Доход потребителя вырос в 1,5 раза. Как изменится его реальный доход?

Запишем первоначальное уравнение бюджетного ограничения У∙Р_у + Х∙Р_х = I. Изменим параметры в соответствии с условием задачи, получим: У∙(2Р_у) + Х∙(2Р_х) = (1,5 I).

Преобразуем (разделим обе части уравнения на 2).

Получим:

У∙Р_у + Х∙Р_х =0,75I

В правой части равенства вместо I стоит 0,75I, т.е. произошло изменение дохода в 0,75 раза. Значит, потребителю доступно в 0,75 раза меньшее количество блага Х и блага У, три четверти прежнего, т.е. реально доход уменьшился на 25%.

Ответ: уменьшился на 25%.

Итак, у потребителя есть цель - получить как можно больше полезности от доступного набора благ. Система предпочтений задана картой кривых безразличия. Потребитель мечтает о наборах благ, лежащих как можно дальше от начала координат (вкуснее, теплее, лучше). Однако его возможности ограничены бюджетом. Потребитель не может выйти за границу бюджета. Поэтому он будет искать такой набор благ, который, с одной стороны, находится в области бюджетных возможностей, а с другой стороны, принадлежит кривой безразличия, наиболее удаленной от начала координат.

Мысля экономически, потребитель сравнивает свои затраты (расходы на покупку товаров) и выгоды (удовлетворение от потребления купленных благ). Он достигнет состояния равновесия, приносящего ему максимальную полезность в том случае, если:

1) уложится в свой бюджет;

2) получит максимально возможную полезность.

Формально эти два условия можно записать следующим образом:

где X и Y – количества двух потребляемых благ, P_x и P_y – цены благ X и Y.

Графически это условие выполняется в точке касания графиков одной из кривых безразличия и бюджетного ограничения. На нашем рисунке равновесие выглядит следующим образом: равновесный и оптимальный набор благ (3Х, 4У) обозначен на графике точкой Е. Она принадлежит одновременно и бюджетному ограничению, и кривой безразличия U₁ и является их точкой касания.

Набор Н, лежащий на кривой безразличия U₀ также принадлежит бюджетному ограничению, но не является оптимальным, так как существует набор Е, доступный при данном бюджете и приносящий б о льшую полезность. Наборы, лежащие на кривой безразличия U_2, желательны для потребителя, но недостижимы с точки зрения бюджета.

Попробуйте провести аналогию оптимального выбора потребителя с задачей сбора рюкзака. Представьте себе, что нужно собраться в поход. В рюкзак необходимо сложить еду и одежду. Объем рюкзака ограничен, поэтому нельзя взять с собой все, что хочется. Если положить много еды, то можно замёрзнуть без одежды. Значит, нужно вынуть часть еды и добавить одежды. Если положить много одежды, то будет тепло, но голодно. Лучше часть одежды заменить едой. Как будем искать оптимум? Точно так же, как рациональный потребитель. Во-первых, возьмем столько вещей, сколько войдет в рюкзак, не больше. Во-вторых, постараемся удовлетворить свои потребности и в еде и одежде.

Точку Е назовем точкой потребительского оптимума, т.к. она расположена на наиболее высокой из доступных потребителю кривых безразличия. Точка Е – точка касания кривой безразличия и прямой бюджетного ограничения, значит, в этой точке бюджетная линия является касательной к кривой безразличия.

Вспомним теперь, что наклон касательной, проведенной к кривой безразличия в данной точке равен предельной норме замещения MRS_ху, а наклон бюджетной линии равен соотношению цен 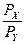. Следовательно, в точке оптимума Е выполняется равенство MRS_ху = .

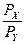Задача 15.

На рисунке изображены четыре набора благ А и Б: 1,2,3,4; бюджетное ограничение I и три кривые безразличия U₀, U₁, U₂.

a) Какие из четырех наборов являются равнополезными?

b) На какие из четырех наборов тратится одинаковое количество денег?

c) Какой набор выберет потребитель при заданных предпочтениях и бюджетном ограничении?

d) Есть ли среди приведенных наборов благ набор, более предпочтительный, чем оптимальный?

Дата добавления: 2014-12-16