Решение. Если бюджетное ограничение 10∙Х + 15∙Y = 90, то на покупку двух товаров выделен доход I = 90

Решение.

Если бюджетное ограничение 10∙ Х + 15∙ Y = 90, то на покупку двух товаров выделен доход I = 90, рынок диктует цены Р_Х = 10, Р_У = 15.

Изобразим данное бюджетное ограничение _.

Для этого найдем максимально возможные количества товаров Х и У.

Х = 90:10 =9;

У = 90: 15 = 6.

Получившиеся крайние точки соединим.

Так как бюджет и цена товара Y не изменились, то максимальное значение Y не изменится и будет равно 6 для всех бюджетных ограничений. А вот максимальное количество товара Х будет изменяться.

Если цена вырастет в 1,5 раза, значит, станет 10·1,5 = 15.

Бюджетное ограничение: 90 = 15∙ Х + 15∙ Y, максимальное Х = 90/15 = 6, т.е. сдвиг влево; значит, прямая провернется по часовой стрелке вокруг точки на оси У.

Если Р_Х = 30, то 90 = 30∙ Х + 15∙ Y, Х_макс = 90/30 = 3. И снова такой же поворот.

Ответ: 15∙ Х + 15∙ Y = 90; 30∙ Х + 15∙ Y = 90.

Задача12.

На графике задана линия бюджетного ограничения. Цена товара Х 100 рублей. Запишите уравнение бюджетного ограничения.

Предположим, что доход потребителя увеличился на 50%, а цены на товары не изменились. Запишите новое уравнение бюджетного ограничения. Постройте эту линию на графике.

Определим первоначальный размер бюджета потребителя. Из графика видно, что истратив все деньги только на товар Х, потребитель может купить 6 единиц товара. Значит I₁ = 6∙100 = 600.

Теперь найдем цену товара Y.

Истратив 600 рублей, потребитель может купить 4 единицы товара Y. Тогда P_Y = 600/4 = 150.

Запишем уравнение для I₁: 100∙ Х + 150∙ Y = 600

Найдем новый доход I₂ = 600∙1,5 = 900 рублей. Доход вырос при неизменных ценах, значит, бюджетная линия сдвинется вправо.

Запишем уравнение для I₂: 100∙ Х + 150∙ Y =900.

Построим новую бюджетную линию.

Если Х = 0, Y = 900:150 = 6.

Если Y = 0, Х = 900:100 = 9.

Ответ: 100∙ Х + 150∙ Y = 600; 100∙ Х + 150∙ Y = 900.

Задача 13.

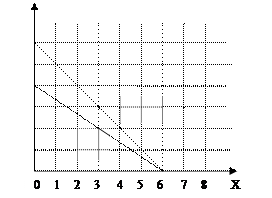На графике показан сдвиг бюджетного ограничения. Первоначально уравнение бюджетного ограничения выглядело как: 10 Х + 15 Y = 60.

Что могло стать причиной изменения положения бюджетной линии (считайте, что изменилось что-то одно)? Запишите уравнение для нового бюджетного ограничения.

Дата добавления: 2014-12-16