
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Шкала отношений МАИ
|
|
|
|
| Степень важности | Определение | Пояснение |
| Одинаковая значимость | Два действия вносят одинаковый вклад в достижение цели | |
| Некоторое преобладание значимости одного действия (показатели фактора) перед другим, слабая зависимость | Опыт и суждения дают легкое предпочтение одному действию перед другим | |
| Существенная или сильная значимость | Опыт и суждения дают сильное предпочтение одному действию перед другим | |
| Очень сильная или очевидная значимость | Предпочтение одного действия над другим очень сильно, его превосходство практически явно | |
| Абсолютная значимость | Свидетельство в пользу предпочтения одного действия другому в высшей степени убедительности | |
| 2,4,6,8 | Промежуточные значения между соседними значениями шкалы | Ситуация, когда необходимо компромиссное решение |
| Обратные величины приведенных чисел | Если действию 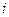 при сравнении с при сравнении с 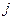 присваивается одно из приведенных выше чисел, то действию присваивается одно из приведенных выше чисел, то действию 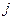 по сравнению с по сравнению с 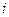 присваивается обратное значение присваивается обратное значение
| Если над диагональю стоит целое число, то под диагональю его обратное значение |
| Рациональное значение | Отношение, возникающее в заданной шкале | Если постулировать согласованность, то для получения матрицы требуется 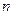 -числовых значений -числовых значений
|
Для обоснования такой шкалы можно привести следующие аргументы. Замечено, что способность человека производить количественные разграничения хорошо представлено пятью определениями: равный, слабый, сильный, очень сильный, абсолютный. Можно принять компромиссные определения между отмеченными соседними, когда нужна большая точность. В целом требуется девять значений, выносимых при сравнении объектов суждений.
Психологический предел – это 7 ±2 предметов при одновременном подтверждении, что если взять 7±2 отдельных предметов и если все они слегка отличаются друг от друга, то понадобится девять точек, чтобы различить их. Использование 1 (единицы) в начале шкалы соответствует отношению значимости объекта относительно самого себя и хорошо вписывается в формальную матричную процедуру МАИ (квадратных, обратно-симметричных матриц с положительными элементами).
В МАИ рекомендованы четыре способа обработки данных.
1. Суммировать элементы каждой строки и нормализовать делением каждой суммы на суммы всех элементов. Сумма полученных результатов равна 1. Первый элемент результирующего вектора будет приоритетом первого объекта (в данном случае 1-го фактора) и т.д.
2. Суммировать элементы каждого столбца и получить обратные элементы этих сумм. Нормализовать их так, чтобы сумма равнялась 1, разделив каждую обратную величину на сумму всех обратных величин.
3. Разделить элементы каждого столбца на сумму элементов этого столбца, т.е. нормализовать столбец. Затем сложить элементы каждой полученной строки и разделить эту сумму на число элементов в строке – усреднение по нормализованным столбцам.
4. Умножить 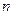 - элементов каждой строки извлечь из произведения корень
- элементов каждой строки извлечь из произведения корень 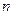 -й степени. Нормализовать полученные числа.
-й степени. Нормализовать полученные числа.
В общем случае, когда матрица  содержит элементы согласованности суждений, указанные способы дают различные результаты векторов приоритетов. Расчет показателей согласованности выполняется следующим образом.
содержит элементы согласованности суждений, указанные способы дают различные результаты векторов приоритетов. Расчет показателей согласованности выполняется следующим образом.
Определяется приближенная оценка главного собственного значения матрицы суждений. Для этого суммируется столбец суждений, а затем сумма первого столбца умножается на величину первой компоненты нормализованного вектора приоритетов, сумма второго столбца – на вторую компоненту и т.д. Затем полученные числа суммируются. Таким образом получаем 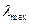 , которая называется оценкой максимума или главного значения матрицы
, которая называется оценкой максимума или главного значения матрицы 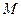 . Это приближение используется для оценки согласованности суждений эксперта. Чем ближе
. Это приближение используется для оценки согласованности суждений эксперта. Чем ближе 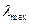 к
к 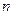 , тем более согласованным является представление в матрице
, тем более согласованным является представление в матрице  суждений. Отклонения от согласованности могут быть выражены величиной, которая называется индексом согласованности (ИС).
суждений. Отклонения от согласованности могут быть выражены величиной, которая называется индексом согласованности (ИС).
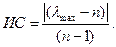
При оценивании величины порога несогласованности суждений для матриц размером от 1 до 15 методом имитационного моделирования получены оценки случайного индекса (СИ). СИ является индексом согласованности для сгенерированной случайным образом (по шкале от 1 до 9) положительной обратно симметричной матрицы. В таблице 7.17) приведены средние (модельные) значения СИ для матриц порядка 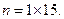
Таблица 7.17
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 1983; Нарушение авторских прав?; Мы поможем в написании вашей работы!