
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. 1. Для расчета параметров а и b линейной регрессии у = а + bх решаем систему нормальных уравнений относительно а и b:
|
|
|
|
1. Для расчета параметров а и b линейной регрессии у = а + bх решаем систему нормальных уравнений относительно а и b:
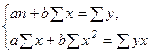
По исходным данным рассчитываем значение всех сумм:
| N п/п | y | x | ух | x2 | y2 | 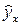
| 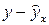
| 
|
| 68,8 | 45,1 | 3102,88 | 2034,01 | 4733.44 | 61,3 | 7,5 | 10,9 | |
| 61,2 | 59,0 | 3610,80 | 3481,00 | 3745,44 | 56,5 | 4,7 | 7,7 | |
| 59,9 | 57,2 | 3426,28 | 3271.84 | 3588.01 | 57,1 | 2.8 | 4»7 | |
| 56,7 | 61,8 | 3504,06 | 3819,24 | 3214,89 | 55,5 | 1,2 | 2,1 | |
| 55,0 | 58,8 | 3234,00 | 3457,44 | 3025,00 | 56,5 | -L5 | 2.7 | |
| 54,3 | 47,2 | 2562,96 | 2227,84 | 2948.49 | 60,5 | -6,2 | 11,4 | |
| 49,3 | 55,2 | 2121,36 | 3047,04 | 2430.49 | 57.8 | -8,5 | 17,2 | |
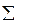
| 405,2 | 384,3 | 22162,34 | 21338,41 | 23685,76 | 405,2 | 0,0 | 56,7 |
Определяем значение параметра b
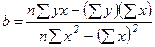 =
= 
Среднее значение переменных
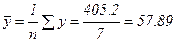 (14)
(14)
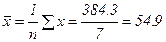 (15)
(15)
С их помощью определим параметр а:
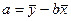 = 57,89 + 0,35 • 54,9 = 77,11
= 57,89 + 0,35 • 54,9 = 77,11
Получаем уравнение линейной регрессии:
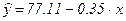
С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 процентных пункта.
Линейный коэффициент парной корреляции:
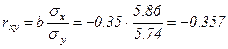
Здесь 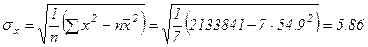
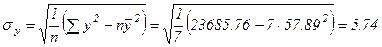
Cвязь умеренная обратная.
Коэффициент детерминации рассчитывается как квадрат коэффициента корреляции:
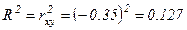
Вариация результата на 12,7% объясняется вариацией фактора х.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения 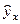 (колонка 6), а также разности между измеренными значениями и рассчитанными (колонка 7). Величины ошибок аппроксимации в колонке 8 рассчитаем как абсолютную величину значений в колонке 7 по отношению к измеренным значениям в колонке 1 в процентах:
(колонка 6), а также разности между измеренными значениями и рассчитанными (колонка 7). Величины ошибок аппроксимации в колонке 8 рассчитаем как абсолютную величину значений в колонке 7 по отношению к измеренным значениям в колонке 1 в процентах:
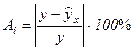
Найдем величину средней ошибки аппроксимации:
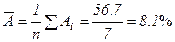
В среднем расчетные значения отклоняются от фактических на 8,1%
Рассчитаем средний коэффициент эластичности линейной регрессии:
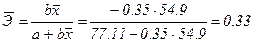
В среднем при увеличении х на 1% значение у уменьшается на 0.33%
Рассчитаем значение F-критерия:
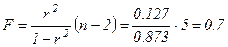
Поскольку 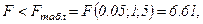 гипотезу Но о случайной природе выявленной зависимости и статистической незначимости параметров уравнения следует принять.
гипотезу Но о случайной природе выявленной зависимости и статистической незначимости параметров уравнения следует принять.
Теперь рассчитаем прогнозное значение 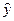 по линейной модели при прогнозном значении фактора
по линейной модели при прогнозном значении фактора 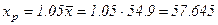 .
.
Прогноз результата: 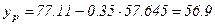 .
.
Определим доверительный интервал для этого прогноза. Для этого нам надо рассчитать стандартную ошибку прогноза по формуле:
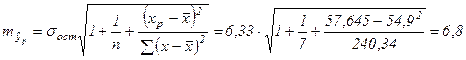
Здесь: 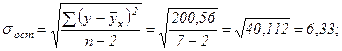
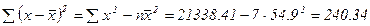
Доверительный интервал рассчитывается так:
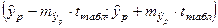
Здесь: 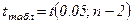 (берем двухстороннее значение t-критерия Стьюдента): t(0,05;5) = 2,57
(берем двухстороннее значение t-критерия Стьюдента): t(0,05;5) = 2,57
Доверительный интервал равен: (39,42;74,38)
Истинное значение прогноза с вероятностью 0,95 попадает в этот интервал.
Задание 1.
Вариант 1.
По территориям Центрального района известны данные за 1995 г.:
| Район | Средний размер назначенных пенсий, тыс.руб., (у) | Прожиточный минимум на одного пенсионера, тыс. руб., (х) |
| Владимирская область | ||
| Ивановская область | ||
| Калужская область | ||
| Костромская область | ||
| г. Москва | ||
| Московская область | ||
| Смоленская область | ||
| Тверская область | ||
| Тульская область | ||
| Ярославская область |
1. Рассчитать параметры парной линейной регрессии.
2. Оценить тесноту связи с помощью показателей корреляции и детерминации.
3.С помощью средних коэффициентов эластичности дать сравнительную оценку силы связи фактора с результатом.
4 Оценить с помощью средней ошибки аппроксимации качество уравнений.
5. С помощью F-критерия Фишера оценить статистическую надежность результатов регрессионного моделирования.
6. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α = 0,05.
Вариант 2.
По территориям Волго-Вятского, Центрально-Черноземного и поволжского районов известны данные за ноябрь 1997 г.
| Район | Потребительские расходы в расчете на душу населения, тыс.руб. (у) | Средняя заработная плата и выплаты социального характера, тыс. руб. (х) |
| Республика Марий Эл | ||
| Республика Мордовия | ||
| Чувашская республика | ||
| Кировская республика | ||
| Нижегородская область | ||
| Белгородская область | ||
| Воронежская область | ||
| Курская область | ||
| Липецкая область | ||
| Тамбовская область | ||
| Республика Татарстан | ||
| Астраханская область | ||
| Волгоградская область | ||
| Пензенская область | ||
| Саратовская область |
1. Рассчитать параметры парной линейной регрессии.
2. Оценить тесноту связи с помощью показателей корреляции и детерминации.
3. С помощью средних коэффициентов эластичности дать сравнительную оценку силы связи фактора с результатом.
4. Оценить с помощью средней ошибки аппроксимациикачествоуравнений.
5. С помощью F-критерия Фишера оценить статистическую надежность результатов регрессионного моделирования.
6. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α = 0,05.
Вариант 3.
По территориям Северного, Северо-западного и Центрального районов известны данные за ноябрь 1997 г.:
| Район | Потребительские расходы на душу населения, тыс.руб., (y) | Денежные доходы на душу населения, тыс, руб., (х) |
| Северный | ||
| Республика Карелия | ||
| Республика Коми | ||
| Архангельская область | ||
| Вологодская область | ||
| Мурманская область | ||
| Северо - Западный | ||
| Ленинградская область | ||
| Новгородская область | ||
| Псковская область | ||
| Центральный | ||
| Брянская область | ||
| Владимирская область | ||
| Ивановская область | ||
| Калужская область | ||
| Костромская область | ||
| Московская область | ||
| Орловская область | ||
| Рязанская область | ||
| Смоленская область | ||
| Тверская область | ||
| Тульская область | ||
| Ярославская область |
1. Рассчитать параметры парной линейной регрессии.
2. Оценить тесноту связи с помощью показателей корреляции и детерминации.
3. С помощью средних коэффициентов эластичности дать сравнительную оценку силы связи фактора с результатом.
4. Оценить с помощью средней ошибки аппроксимации качество уравнений.
5. С помощью F-критерия Фишера оценить статистическую надежность результатов регрессионного моделирования
6. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 4% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α = 0,05.
Вариант 4.
По территориям Восточно-Сибирского и Дальневосточного районов известны данные за ноябрь 1997 г.:
| Район | Потребительские расходы на душу населения, тыс.руб., (у) | Денежные расходы на душу населения, тыс. руб., (х) |
| Восточно-Сибирский | ||
| Республика Бурятия | ||
| Республика Тыва | ||
| Республика Хакасия | ||
| Красноярский край | ||
| Иркутская область | ||
| Усть-Ордынский Бурятский автономный округ | ||
| Читинская область | ||
| Дальневосточный | ||
| Республик Саха (Якутия) | ||
| Еврейская авт. обл. | ||
| Приморский край | ||
| Хабаровский край | ||
| Амурская область | ||
| Камчатская область | ||
| Магаданская область | ||
| Сахалинская область |
1. Рассчитать параметры парной линейной регрессии.
2. Оценить тесноту связи с помощью показателей корреляции и детерминации.
3. С помощью средних коэффициентов эластичности дать сравнительную оценку силы связи фактора с результатом.
4. Оценить с помощью средней ошибки аппроксимациикачествоуравнений.
5. С помощью F-критерия Фишера оценить статистическую надежность результатов регрессионного моделирования.
6. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 5% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α = 0,05
Вариант 5.
По территориям Уральского и Западно-Сибирского районов известны данные за ноябрь 1997 г.:
| Район | Потребительские расходы на душу населения, тыс.руб., (у) | Денежные расходы на душу населения, тыс. руб., (х) |
| Уральский | ||
| Респ. Башкортостан | ||
| Удмуртская область | ||
| Курганская область | ||
| Оренбургская область | ||
| Пермская область | ||
| Свердловская область | ||
| Челябинская область | ||
| Западно-Сибирский | ||
| Республика Алтай | ||
| Алтайский край | ||
| Кемеровская область | ||
| Новосибирская область | ||
| Омская область | ||
| Томская область | ||
| Тюменская область |
1. Рассчитайте параметры парной линейной регрессии.
2. Оценить тесноту связи с помощью показателей корреляции и детерминации.
3. С помощью средних коэффициентов эластичности дать сравнительную оценку силы связи фактора с результатом.
4. Оценить с помощью средней ошибки аппроксимации качество уравнений.
5. С помощью F-критерия Фишера оценить статистическую надежность результатов регрессионного моделирования.
6. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 8% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α = 0,05
Второе задание предполагает изучение многофакторного корреляционно-регрессионного анализа и расчет характеристик уравнения множественной регрессии с целью получения достоверных статистических выводов о наличии зависимости между результативным и факторными признаками.
Уравнение множественной регрессии имеет следующий вид:
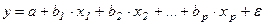 (16)
(16)
где у - зависимая переменная (результативный признак);
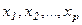 - независимые переменные (факторы);
- независимые переменные (факторы);
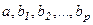 - параметры;
- параметры;
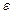 - случайная величина (ошибка).
- случайная величина (ошибка).
Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений строится следующая система нормальных уравнений, решение которых позволяет получить оценки параметров регрессии:
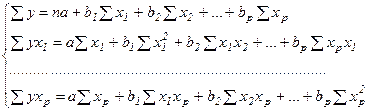 (17)
(17)
Параметры этой системы могут быть найдены, например, методом К. Гаусса.
Другой вид уравнения множественной регрессии – уравнение регрессии в стандартизованном масштабе:
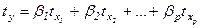 (18)
(18)
где 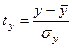 ,
, 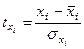 - стандартизованные переменные;
- стандартизованные переменные;
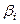 - стандартизованные коэффициенты регрессии.
- стандартизованные коэффициенты регрессии.
К уравнению множественной регрессии в стандартизованном масштабе применим МНК.
Связь коэффициентов множественной регрессии 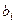 со стандартизованными коэффициентами
со стандартизованными коэффициентами 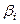 описывается соотношением
описывается соотношением
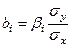 (19)
(19)
Параметр а определяется как
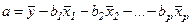 (20)
(20)
Средние частные коэффициенты эластичности для линейной регрессии рассчитываются по следующей формуле:
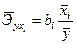 (21)
(21)
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции:
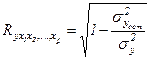 (22)
(22)
Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:
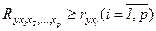
Индекс множественной корреляции для стандартизованном масштабе можно записать в виде
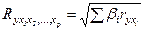 (23)
(23)
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора 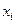 определяются по следующим формулам:
определяются по следующим формулам:
Частный коэффициент корреляции первого порядка между признаками  и у при исключении влияния признака
и у при исключении влияния признака 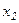 вычисляют по формуле:
вычисляют по формуле:
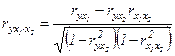 ; (24)
; (24)
то же - зависимость у от 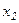 при исключении влияния
при исключении влияния  :
:
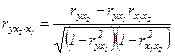 (25)
(25)
Взаимосвязь факторных признаков при устранении влияния результативного признака:
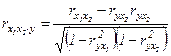 , (26)
, (26)
где r - парные коэффициенты корреляции между соответствующими признаками.
Частные коэффициенты корреляции изменяются в пределах от -1 до 1.
Парные коэффициенты корреляции рассчитываются по следующим формулам:
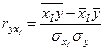 ; (27)
; (27)
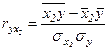 ; (28)
; (28)
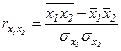 (29)
(29)
Среднеквадратические отклонения вычисляются по формулам:
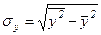 (30)
(30)
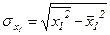 (31)
(31)
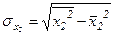 (32)
(32)
На основе парных коэффициентов корреляции и средних квадратических отклонений можно рассчитать параметры уравнения двухфакторной связи по формулам:
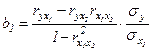 ; (33)
; (33)
 ; (34)
; (34)
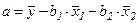 (35)
(35)
Качество построенной модели в целом оценивает коэффициент (индекс) детерминации. Коэффициент множественной детерминации рассчитывается как квадрат индекса множественной корреляции:
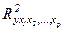 (36)
(36)
Значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера:
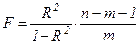 (37)
(37)
где n - число наблюдений;
m - число факторов (независимых переменных в уравнении).
Решение типового примера 2.
По 20 предприятиям региона (табл. 1) изучается зависимость выработки продукции на одного работника у (тыс. руб.) от ввода в действие новых основных фондов  (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих
(% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих 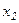 (%).
(%).
Таблица 1
| Номер предприятия | у | 
| 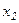
|
| 7.0 | 3,9 | 10,0 | |
| 7.0 | 3.9 | 14,0 | |
| 7,0 | 3.7 | 15.0 | |
| 7,0 | 4,0 | 16.0 | |
| 7,0 | 3,8 | 17,0 | |
| 7,0 | 4,8 | 19,0 | |
| 8,0 | 5,4 | 19,0 | |
| 8,0 | 4,4 | 20,0 | |
| 8,0 | 5,3 | 20,0 | |
| 10,0 | 6,8 | 20,0 | |
| 9,0 | 6,0 | 21,0 | |
| 11,0 | 6,4 | 22,0 | |
| 9,0 | 6,8 | 22,0 | |
| 11,0 | 7,2 | 25,0 | |
| 12,0 | 8,0 | 28,0 | |
| 12,0 | 8,2 | 29,0 | |
| 12,0 | 8,1 | 30,0 | |
| 12,0 | 8,5 | 31,0 | |
| 14,0 | 9,6 | 32,0 | |
| 14,0 | 9,0 | 36,0 |
Требуется:
1. Построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров.
2. Рассчитать средние частные коэффициенты эластичности.
3. Определить стандартизованные коэффициенты регрессии.
В пп. 2. и 3. на основе полученных результатов сделать вывод о силе связи результата с каждым из факторов.
4. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.
5. Дать оценку полученного уравнения на основе коэффициента детерминации и общего F-критерия Фишера.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 2740; Нарушение авторских прав?; Мы поможем в написании вашей работы!