Определимых задач на примере кронштейна

Методические указания к расчету статически

Общие положения

Осевое растяжение-сжатие

Осевое растяжение-сжатие - это напряженно-деформированное состояние стержня, при котором из всех 6-ти внутренних силовых факторов не равен нулю только один - продольная сила N.

Задача этой темы сводится к проверке прочности и жесткости стержней или стержневых систем Решение задач начинается с опре­деления продольной силы N. Если для нахождения продольной силы N во всех стержнях системы достаточно уравнений статики, то систе­ма называется статически определимой, если нет - статически неоп­ределимой.

Для нахождения продольной силы применяют метод сечений. Зная продольную силу, можно рассчитать нормальные напряжения, и, сравнив их с допускаемыми, проверить прочность стержня по условию (2.2.1), или по этому же условию рассчитать площадь се­чения стержня, при котором его прочность будет обеспечена.

Зная продольную силу N, размеры стержня (ℓ- длину и F -площадь поперечного сечения), можно по формуле (2.2.2) рассчитать удлинение или укорочение стержня и сравнить их с допускаемым, проверить жесткость стержня.

Методические указания к решению статически определимых за­дач и пример даны в подразделах 2.2 и 2.3.

Решение статически неопределимых задач усложняется необ­ходимостью нахождения неизвестных усилий, число которых больше, чем число уравнений статики, используемых для их нахождения.

Методические указания и пример решения статически неопре­делимых задач даны в подразделах 2.4 и 2.5.

1. Найти продольные усилия в стержнях кронштейна методом сечений. Рассмотреть равновесие отсеченного узла. Усилия в стержнях принять растягивающими, направленными от узла. Составить уравнения равновесия на координатные оси:

ZY = 0 и ΣX = 0.

2. Определить из условия прочности (2.2.1) требуемые площади F поперечных сечений стального и деревянного стержней:

│σ│ = (2.2.1)

где │σ│ и [σ] - нормальные действующие и допускаемые напряжения.

3. Подобрать по сортаменту стальной равнополочный уголок с указанием номера и размеров уголка по требуемой площади 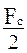. Вычислить требуемую сторону квадрата или требуемый диаметр поперечного сечения деревянного стержня. Округлить требуемые размеры стороны квадрата и диаметр до целых сантиметров.

4. Определить линейное перемещение узла (рис. 3). Предварительно вычислить продольные удлинение или укорочение стержней кронштейна, учитывая фактически принятые площади сечений по формуле

Δℓ_i = 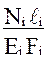(2.2.2)

5. Построить план перемещений узла (рис. 3). В качестве полюса принять начальное положение узла. Из точки полюса параллельно соответствующим стержням в принятом масштабе отложить удлинения и укорочения стержней Δℓ_i. Деформация стержней кронштейна под нагрузкой Р сопровождается одновременно их поворотом в шарнирном узле. Поэтому через концы удлинений или укорочений Δℓ_i необходимо провести перпендикуляры и найти точку их пересечения. Отрезок плана перемещений, соединяющий полюс и точку пересечения перпендикуляров, является истинным линейным перемещением узла кронштейна.

Дата добавления: 2014-12-17