Неопределимых стержневых систем

Примеры расчета статически

Пример 2.5.1.

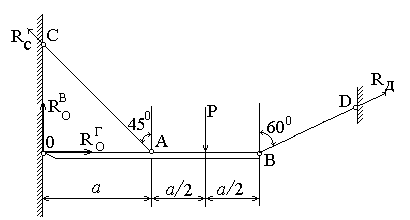
Абсолютно жесткий брус закреплен с помощью шарнирно-неподвижной опоры и двух стальных стержней одинаковой длины ℓ и одинакового поперечного сечения F = 5 см² (рис. 4а). Определить усилия и напряжения в стержнях от на грузки Р = 50 кН.

Решение.

1. Степень статической неопределимости системы: n = n_р – n_у = 4 – 3 = 1,

где n_р = 4, так как имеют место реакции R_c, R_d, 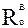и ;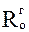

n_у = 3, т.к. для плоской системы в общем случае могут быть использованы 3 уравнения статики.

Система один раз статически неопределима.

2. Применяем метод сечений. Продольные усилия в стержнях АС и BD принимаем растягивающими и обозначим N₁ и N₂. Составим уравнение равновесия

ΣМ₀ = 0, N₁cos45°α + N₂cos60⁰2α – P · I,5α = 0 (2.5.1)

Можно составить еще два уравнения равновесия ΣХ = 0 и ΣY = 0, но в них войдут еще два неизвестных усилия - реакции в опоре О, которые нас не интересуют. Имеем одно уравнение с двумя неизвестными. Система один раз статически неопределима.

3. Для составления дополнительного уравнения перемещений рассмотрим деформацию системы. После нагружения системы силой Р брус ОАВ займет положение ОА₁В₁ (рис 46). Стержни удлиняются Δℓ₁ = АА₂ и Δℓ₂ = ВВ₂. Тогда из подобия треугольников ОАА₁ и ОВВ₁ получим

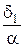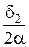= или =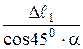

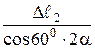
или 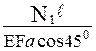= 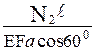(2.5.2)

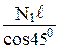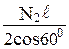= ; = N₂

4. Решая совместно полученные уравнения равновесия (2.5.1) и перемещений (2.5.2), найдем N₁ и N₂:

N₁ · 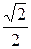+ 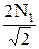· · 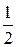2 = 1,5 Р

Тогда N₁ = 0,707 Р · 50 = 35,35 кН,

N₂ = P = 50 kH.

5. Напряжения в стержнях:

σ₁ = 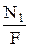= = 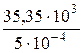7,07 · 10⁷ Па = 70,7 МПа,

σ₂ = 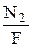= = 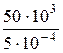10 · 10⁷ Па = 100 МПа.

а)

б)

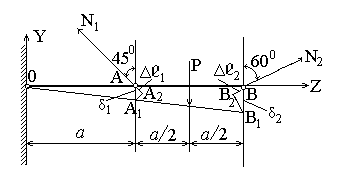
Рис. 4

Пример 2.5.2.

Абсолютно жесткий брус подвешен на трех стальных стержнях одинаковой длины ℓ и одинакового поперечного сечения F = 4 см² (рис. 5а). Определить усилия и напряжение, возникающие в стержнях от нагревания третьего стержня на 60°. Коэффициент линейного расширения α_ст = 12,5·10^–6 1/град, Е_ст = 2 10⁵ МПа.

Решение:

1. Степень статической неопределимости системы:

n = n_р – n_у = 3 – 2 = 1,

где n_р = 3, число реакций;

n_у = 2, число уравнений равновесия статики, которые могут быть использованы. В данном случае только два, все силы действующие на плоскую систему параллельны.

а) б)

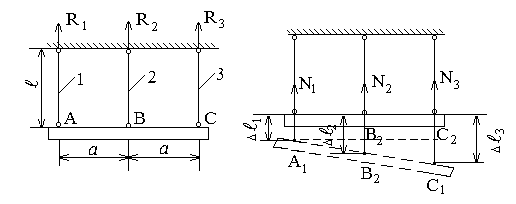
Рис. 5

2. Предположим, что все стержни растянуты (рис. 5б). Составим уравнения равновесия:

åУ = 0, N₁ + N₂ + N₃ = 0 (2.5.3)

åM_A = 0, N₂× а + N₃×2 а = 0, или N₂ = - 2N₃ (2.5.4)

Система один раз статически неопределима, так как два уравнения равновесия содержат три неизвестные усилия.

3. Составим уравнение перемещений. После нагревания третьего стержня брус АВС займет новое положение А₁В₁С₁. Тогда из подобия треугольников А₁С₁С₂ и А₁В₁В₂ получим зависимости:

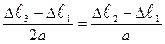(2.5.5)

Изменение длины третьего стержня произойдет в результате его нагрева и возникающего в нем усилия N₃, т.е. 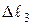= 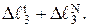Следовательно,

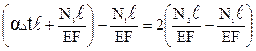уравнение перемещений примет вид

или αΔtEF + N₃ – N₁ = 2N₂ –2N₁ (2.5.6)

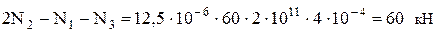4. Решая совместно уравнения (1), (2) и (4), найдем:

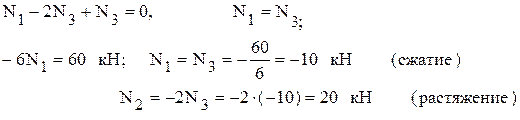
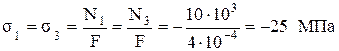5. Напряжения в стержнях:

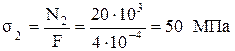
Пример 2.5.3.

В системе из трех стержней (рис. 6а) длина среднего стержня меньше проектной длины на d = 1 мм. Наклонные стержни стальные с площадью F_ст = 10 см², вертикальный стержень медный с площадью F_м = 25 см². Определить усилия и напряжения в стержнях после сборки конструкции. Е_ст = 2×10⁵ МПа; Е_м = 1×10⁵ МПа; а = 1м; b = 1м.

Решение:

1. Степень статической неопределимости системы ,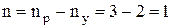

где 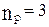- число реакций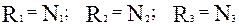

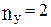– число уравнений статики, которые могут быть использованы для решения системы.

Так как все силы сходятся в одной точке, то сумма моментов этих сил относительно любой точки системы тождественно равна 0

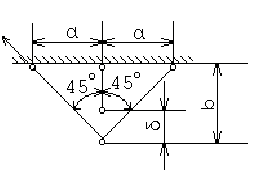
а) б)

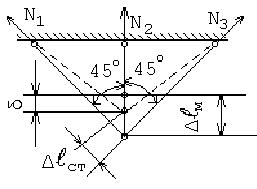
Рис. 6

В этом случае для плоской системы остается только два уравнения равновесия статики.

Схему системы после сборки (рис. 6б) рисуем, предполагая, что в действительности стержень испытывает сжатие.

2. Уравнения равновесия статики имеют вид:

åХ = 0 –N₁sin45° + N₃sin45° = 0 N₁ = N₃ (2.5.7)

åY = 0 N₁cos45°+N₂+N₃cos45° = 0 (2.5.8)

Дата добавления: 2014-12-17