ТЕМА 5. Диференціальні рівняння Вищих порядків

РОЗДІЛ 2. ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ ВИЩИХ ПОРЯДКІВ

ВПРАВИ

ПИТАННЯ ДЛЯ САМОПЕРЕВІРКИ

Приклад 4.4.

Розв’язати рівняння .

● Маємо рівняння Клеро. Загальний розв’язок, згідно з (12), має вигляд .

Особливий розв’язок заданого рівняння дістанемо з (13): , звідки Це рівняння обвідної сім’ї прямих . ●

1. Записати ДР першого порядку,яке містить лише та його загальний розв’язок.

2. Записати ДР першого порядку,яке не залежить від x та його параметричні рівняння.

3. Записати ДР першого порядку,яке не залежить від y та його параметричні рівняння.

4. Записати загальний вигляд рівняння Лагранжа.

5. Записати загальний вигляд рівняння Клеро.

І. Розв’язати рівняння

1. ; 2. ; 3. ; 4. ; 5. ; 6. ; 7. ; 8. ; 9. ; 10. ;

11. ; 12. ; 13. ; 14. ; 15. ; 16. ; 17. ; 18. ; 19. ; 20. .

ТЕОРЕТИЧНИЙ МАТЕРІАЛ

5.1. Основні поняття і означення. Задача Коші

Розглянемо диференціальні рівняння, які містять похідні вищих порядків. Порядок найвищої похідної невідомої функції, що входить у диференціальне рівняння, називається порядком цього рівняння.

Зокрема, диференціальне рівняння n -го порядку має вигляд

, (1)

де 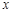– незалежна змінна, – невідома функція, – відома функція.

У рівняння (1) похідна n -го порядку має справді входити, тоді як наявність у ньому решти змінних, тобто ,…, , необов’язкова.

Рівняння (1), не розв’язане відносно старшої похідної , називається неявним диференціальним рівнянням.

Нормальним або явним диференціальним рівнянням n -го порядку називається рівняння (1), розв’язане відносно :

. (2)

Розв’язком рівняння (2) на деякому інтервалі називається n разів неперервно диференційована на цьому інтервалі функція 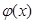, яка при підстановці в дане рівняння обертає його в тотожність по , тобто

.

Графік розв’язку диференційованого рівняння (1) або (2) називається його інтегральною кривою.

Задача Коші для диференціальних рівнянь вищих порядків:

Для рівняння (2) серед усіх розв’язків рівняння знайти такий розв’язок , який при задовольняє такі умови:

або

, (3)

де - довільні наперед задані дійсні числа. Умови (3) називають початковими умовами рівняння (2). Зокрема, для рівняння другого порядку , початкові умови при мають вигляд .

В загальному випадку розв’язок диференціального рівняння n -го порядку знаходиться в результаті n послідовних інтегрувань, тому загальний розв’язок рівняння (2) містить n довільних сталих, тобто має вигляд

. (4)

Якщо загальний розв’язок знаходиться в неявній формі

,

то його називають загальним інтегралом рівняння (2).

Частинний розв’язок або частинний інтеграл знаходять із загального, якщо у співвідношенні (4) кожній довільній сталій надати конкретного числового значення. З погляду геометрії загальним розв’язком рівняння (2) є n-параметрична сім’я інтегральних кривих, залежних від n параметрів , а частинний розв’язок – окрема крива з цієї сім’ї.

Таким чином, розв’язати (проінтегрувати) диференціальне рівняння n -го порядку – це означає: 1) знайти його загальний розв’язок; 2) із загального розв’язку виділити частинний розв’язок, який задовольняє початкові умови, якщо такі умови задані.

Дата добавления: 2014-12-17