Дифференциальные уравнения. Основные понятия и определения

Основные понятия и определения

Уравнение, связывающее независимую переменную 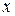, функцию этой переменной 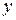и ее производные, называется дифференциальным.

Порядком дифференциального уравнения называется наивысший порядок производной, входящей в это уравнение. Например, уравнение 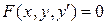–уравнение 1-го порядка, 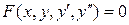–уравнение 2-го порядка и т. д.

Частным решением дифференциального уравнения называется функция 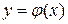, обращающая это уравнение в тождество.

Рассмотрим уравнение 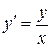. Это дифференциальное уравнение 1-го порядка. Функция 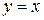будет его решением, так как 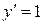и подстановка этой функции в уравнение дает 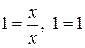, т.е. эта функция обратила данное уравнение в тождество.

Легко проверить, что 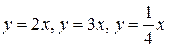и вообще, 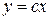–будут решением данного уравнения.

Функция 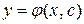называется общим решением дифференциального уравнения 1-гопорядка, если при любом значении произвольного постоянного с она обращает это уравнение в тождество и специальным подбором постоянного с из этой функции можно получить любое частное решение. Так, в приведенном примере, функции 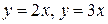и т. д. являются частными решениями, а функция 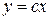– общим решением рассматриваемого уравнения.

График решения дифференциального уравнения называется интегральной кривой. Частные решения определяют конкретные интегральные кривые, а общее решение – семейство всех интегральных кривых. Интегральная кривая, определяющая частное решение и удовлетворяющая начальному условию 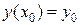, – это кривая из семейства интегральных кривых, проходящая через точку .

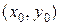Пусть начальные условия для рассматриваемого примера будут 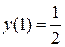. Подставляя в общее решение 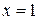и 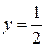, получим 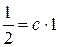, откуда 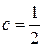, и функция 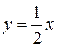будет являться частным решением, удовлетворяющим заданному начальному условию. Из всех интегральных прямых мы взяли ту, которая проходит через точку .

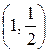Аналогичным образом будем определять позже частные и общие решения для уравнений более высокого порядка. Рассмотрим конкретные виды дифференциальных уравнений и методы их решения.

Дифференциальные уравнения с разделяющимися переменными

В общем виде дифференциальное уравнение первого порядка может быть записано в неявном 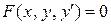или в явном виде 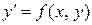. Если это уравнение может быть представлено в виде 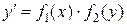, то оно называется уравнением с разделяющимися переменными. Действительно, в этом случае можно провести следующие преобразования: 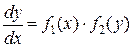, , 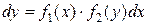, 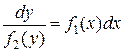(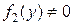). И получим уравнение с уже разделенными переменными. Интегрируя левую и правую части уравнения с разделенными переменными, получим 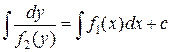. Выполняя интегрирование, найдем связь между и 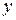в виде 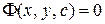, которая называется общим интегралом данного уравнения. Если из последнего уравнения выразить 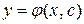, то получим общее решение данного уравнения.

Замечание. Уравнение с разделяющимися переменными может быть записано в виде 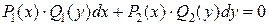. К уравнению с разделенными переменными приходим аналогично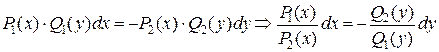 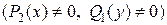и теперь нужно, как и раньше, проинтегрировать обе части полученного равенства.

Например,

; ; ; .

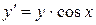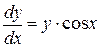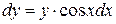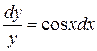Интегрируем последнее уравнение

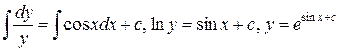. Получено общее решение данного уравнения. v

Дата добавления: 2014-12-17