
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейные уравнения первого порядка
|
|
|
|
Однородные уравнения первого порядка
Пусть дано дифференциальное уравнение первого порядка 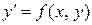 . Если функция
. Если функция 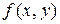 удовлетворяет условию
удовлетворяет условию 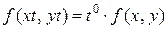 , т.е. является однородной функцией нулевого порядка, то данное уравнение называется однородным.
, т.е. является однородной функцией нулевого порядка, то данное уравнение называется однородным.
Полагая в равенстве 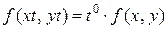 переменную
переменную 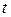 равной
равной 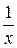 , получим
, получим 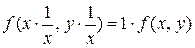 , или
, или 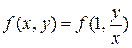 . Это означает, что однородная функция нулевого порядка может быть выражена через отношение
. Это означает, что однородная функция нулевого порядка может быть выражена через отношение 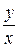 . Поэтому для решения данного уравнения применяют подстановку
. Поэтому для решения данного уравнения применяют подстановку 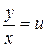 или
или  , где
, где 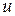 – неизвестная функция от
– неизвестная функция от 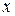 . Найдя ее, найдем и
. Найдя ее, найдем и 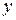 – решение данного уравнения.
– решение данного уравнения.
Пример. Решить уравнение 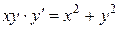 .
.
Решение. Находим 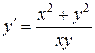 ;
; 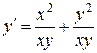 ;
; 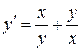 . Так как правая часть зависит от
. Так как правая часть зависит от 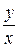 , то уравнение является однородным. Делаем подстановку:
, то уравнение является однородным. Делаем подстановку: 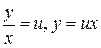 , тогда
, тогда 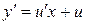 и получаем
и получаем 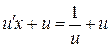 ,
, 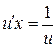 ,
, 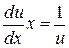 ,
, 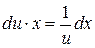 ,
, 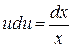 , интегрируя, получим
, интегрируя, получим 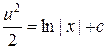 ,
, 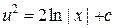 ,
, 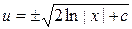 . Следовательно,
. Следовательно, 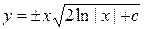 — общее решение данного уравнения. v
— общее решение данного уравнения. v
Линейными уравнениями первого порядка называется уравнение вида 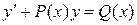 , где
, где 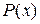 и
и 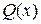 — заданные непрерывные функции от
— заданные непрерывные функции от 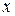 .
.
Для решения таких уравнений делаем подстановку 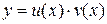 . Тогда
. Тогда 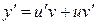 и уравнение примет вид
и уравнение примет вид 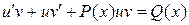 или
или  . Выберем теперь
. Выберем теперь 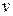 так, чтобы
так, чтобы 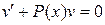 . Для этого надо решить последнее уравнение. Оно является уравнением с разделяющимися переменными и решается просто. Найдя
. Для этого надо решить последнее уравнение. Оно является уравнением с разделяющимися переменными и решается просто. Найдя 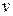 , из уравнения
, из уравнения  находим функцию
находим функцию 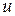 , а значит, и
, а значит, и 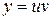 . Таким образом, уравнение распадается на систему двух более простых уравнений с разделяющимися переменными.
. Таким образом, уравнение распадается на систему двух более простых уравнений с разделяющимися переменными.
Пример. Найти общее решение уравнения 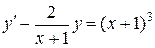 .
.
Решение. Сделаем подстановку 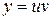 , где
, где 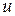 и
и 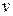 – неизвестные пока функции от
– неизвестные пока функции от 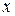 . Тогда
. Тогда 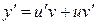 и уравнение принимает вид:
и уравнение принимает вид:
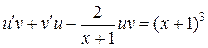 или
или 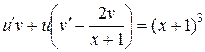 .
.
Выбираем 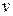 так, чтобы
так, чтобы 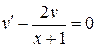 . Решаем это уравнение
. Решаем это уравнение 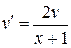 ,
, 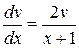 ;
; 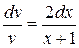 ; интегрируя, получим:
; интегрируя, получим: 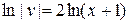 ;
; 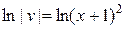 ;
; 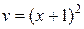 . Подставляя это значение в равенство
. Подставляя это значение в равенство 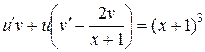 , получим:
, получим:
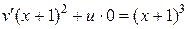 ;
; 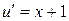 ;
; 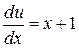 ;
; 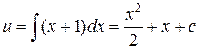 .
.
Таким образом, 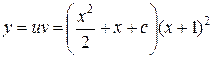 – общее решение данного уравнения. v
– общее решение данного уравнения. v
Замечание. Уравнение вида  при
при 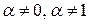 не является линейным. Оно называется уравнением Бернулли, но решается так же, как и линейное, подстановкой
не является линейным. Оно называется уравнением Бернулли, но решается так же, как и линейное, подстановкой 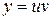 .
.
Дифференциальные уравнения высших порядков
Перейдем к рассмотрению дифференциальных уравнений высших порядков, начиная со второго. Дифференциальные уравнения второго порядка имеют вид
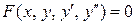 .
.
Общим решением дифференциального уравнения второго порядка называется функция  , которая при любых значениях произвольных постоянных обращает уравнение в тождество и из которой специальным подбором
, которая при любых значениях произвольных постоянных обращает уравнение в тождество и из которой специальным подбором 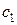 и
и 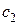 можно получить любое частное решение.
можно получить любое частное решение.
Рассмотрим некоторые частные случаи уравнения второго порядка, общее решение которых находится понижением порядка уравнения.
1. Уравнение вида 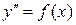 . Имеем
. Имеем 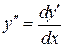 , тогда
, тогда 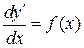 ,
, 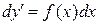 ,
, 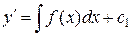
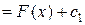 . Далее
. Далее 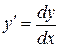 , поэтому
, поэтому 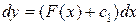 и
и 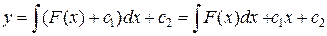 , где
, где  — одна из первообразных функций для
— одна из первообразных функций для  .
.
Пример. Решить дифференциальное уравнение второго порядка 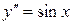 .
.
Решение. 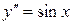 ;
; 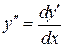 ;
; 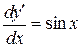 ;
;  . Интегрируя, находим
. Интегрируя, находим 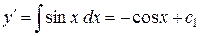 .Далее
.Далее 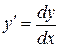 ;
; 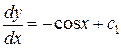 ;
; 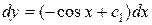 , интегрируя, получаем
, интегрируя, получаем
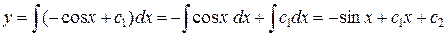 – общее решение. v
– общее решение. v
Замечание. Аналогичным образом решаются уравнения указанного вида более высокого порядка.
2. Уравнения, явно не содержащие неизвестной функции 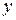 :
: 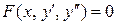 .
.
Делая замену 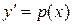 , получим
, получим 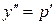
 , и уравнение принимает вид
, и уравнение принимает вид 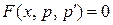 . Решая это уравнение первого порядка, находим функцию
. Решая это уравнение первого порядка, находим функцию 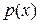 , азатем, из подстановки
, азатем, из подстановки 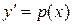 , путем интегрирования находим неизвестную функцию
, путем интегрирования находим неизвестную функцию 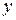 .
.
Пример. Найти общее решение уравнения 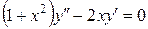 .
.
Решение. Делаем подстановку 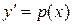 . Тогда
. Тогда 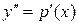 . Получим
. Получим
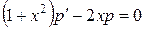 ,
, 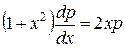 ;
; 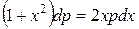 ;
; 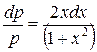 .
.
Интегрируя последнее уравнение, найдем 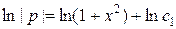 ;
; 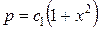 . Так как
. Так как 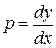 , то
, то 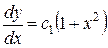 ;
; 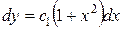 , откуда
, откуда 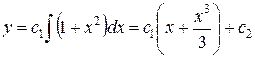 – общее решение данного уравнения. v
– общее решение данного уравнения. v
3. Уравнения, явно не содержащие независимую переменную 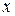 :
: 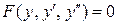 .
.
В этом случае, исходя из подстановки 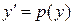 , где
, где 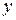 – функция от
– функция от 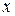 ,находим
,находим 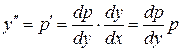 . Подставляя в исходное уравнение значения
. Подставляя в исходное уравнение значения 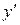 и
и 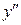 ,получаем уравнение первого порядка относительно функции
,получаем уравнение первого порядка относительно функции 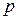 ,найдя которую, из подстановки
,найдя которую, из подстановки 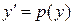 , находим
, находим 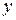 .
.
Пример. Найти общее решение уравнения 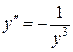 .
.
Решение. Делая подстановку 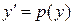 ,
, 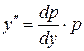 , получим
, получим 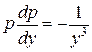 ,
, 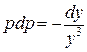 . Интегрируем обе части уравнения:
. Интегрируем обе части уравнения: 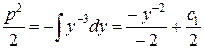 ;
; 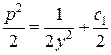 ;
; 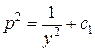 ;
;  . Так как
. Так как 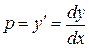 , то
, то  ;
; 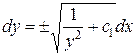 ;
; 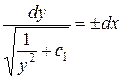 ;
; 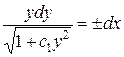 . Интегрируя, найдем:
. Интегрируя, найдем:
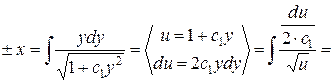
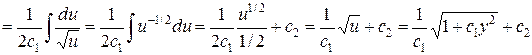 .
.
Итак, общий интеграл данного уравнения 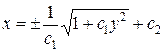 . v
. v
Линейные уравнения второго порядка
Рассмотрим теперь важный класс уравнений вида
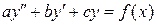 . (8.1)
. (8.1)
Если 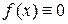 , то данное уравнение называется однородным. В противном случае, данное уравнение называется неоднородным.
, то данное уравнение называется однородным. В противном случае, данное уравнение называется неоднородным.
Общее решение неоднородного уравнения имеет вид 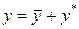 , где
, где 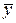 –общее решение соответствующего однородного уравнения:
–общее решение соответствующего однородного уравнения: 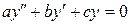 , а
, а 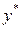 –некоторое частное решение исходного уравнения.
–некоторое частное решение исходного уравнения.
Будем рассматривать наиболее часто встречающиеся в практике случаи, когда коэффициенты 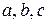 являются постоянными числами, а правая часть имеет простой (специальный) вид.
являются постоянными числами, а правая часть имеет простой (специальный) вид.
К таким уравнениям приводят многие физические задачи, решение которых, например, основано на втором законе механики 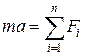 , где
, где 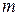 – масса системы,
– масса системы, 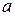 – ускорение,
– ускорение, 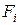 – действующие силы.
– действующие силы.
Если, например, на некоторую систему действуют силы  (сила, пропорциональная скорости движения) и
(сила, пропорциональная скорости движения) и 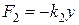 (сила, восстанавливающая отклонение от положения равновесия), при этом внешнее возмущение описывается функцией
(сила, восстанавливающая отклонение от положения равновесия), при этом внешнее возмущение описывается функцией 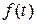 , то, учитывая, что
, то, учитывая, что 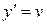 , а
, а 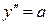 , получаем
, получаем
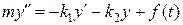 или
или 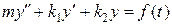 ,
,
а это, с точностью до обозначений, совпадает с общим видом линейных уравнений второго порядка (8.1).
Решение уравнения (8.1) ищем в виде 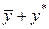 . Для нахождения
. Для нахождения 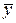 составляем характеристическое уравнение
составляем характеристическое уравнение 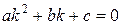 ,находим его корни
,находим его корни 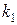 и
и 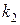 и в зависимости от их значений определяем
и в зависимости от их значений определяем 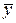 . Правило нахождения
. Правило нахождения 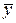 укажем в таблице 1.
укажем в таблице 1.
Таблица 1
Характеристическое уравнение
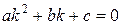 , , 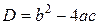
| Общее решение однородного уравнения 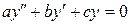
|
1. 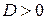 , ,  –
действительные и различные –
действительные и различные
|
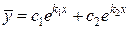
|
2. 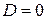 , , 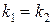 –
действительные и равные –
действительные и равные
|
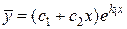
|
3. 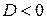 , , 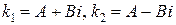 –
комплексно - сопряженные –
комплексно - сопряженные
|
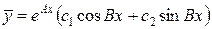
|
При нахождении 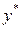 будем исходить из того, что правая часть уравнения
будем исходить из того, что правая часть уравнения  имеет специальный вид:
имеет специальный вид: 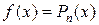 ;
; 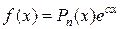 ;
; 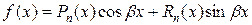 ;
; 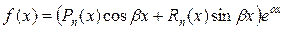 , где
, где 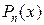 и
и 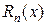 –заданные многочлены в степени
–заданные многочлены в степени 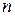 .
.
Например, 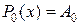 — многочлен нулевой степени,
— многочлен нулевой степени, 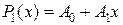 — многочлен первой степени,
— многочлен первой степени, 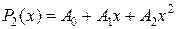 — многочлен второй степени и так далее. Соответствующие значения для
— многочлен второй степени и так далее. Соответствующие значения для 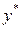 укажем в таблице 2.
укажем в таблице 2.
Таблица 2

| 
|
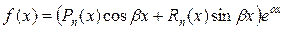
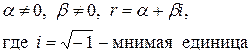
| 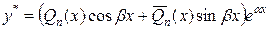 , если число , если число 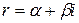 не является корнем характеристического уравнения, и не является корнем характеристического уравнения, и
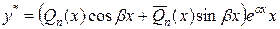 , если число , если число 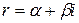 является корнем характеристического уравнения является корнем характеристического уравнения
|
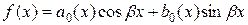 , ,
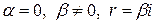
| 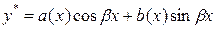 , если число , если число 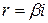 не является корнем характеристического уравнения, и не является корнем характеристического уравнения, и
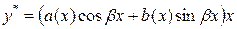 , если число , если число 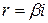 является корнем характеристического уравнения является корнем характеристического уравнения
|
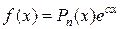 , ,
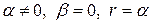
| 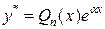 , если среди корней характеристического уравнения нет числа , если среди корней характеристического уравнения нет числа 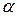 ; ;
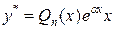 , если , если  является однократным корнем характеристического уравнения; является однократным корнем характеристического уравнения;
 , если , если  является двукратным корнем характеристического уравнения является двукратным корнем характеристического уравнения
|
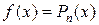 , ,
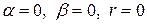
| 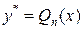 , если среди корней характеристического уравнения нет числа 0; , если среди корней характеристического уравнения нет числа 0;
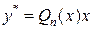 ,если число ,если число 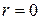 является однократным корнем характеристического уравнения; является однократным корнем характеристического уравнения;
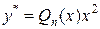 , если число , если число 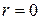 является двукратным корнем характеристического уравнения является двукратным корнем характеристического уравнения
|
В выражениях для 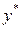 содержится функция
содержится функция  , которая представляет собой многочлен степени
, которая представляет собой многочлен степени 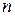 с неизвестными коэффициентами:
с неизвестными коэффициентами: 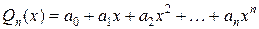 . Задача состоит в том, чтобы найти эту функцию, т.е. определить неизвестные коэффициенты
. Задача состоит в том, чтобы найти эту функцию, т.е. определить неизвестные коэффициенты 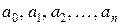 . Для этого нужно вычислить
. Для этого нужно вычислить  ,
,  , подставить значения
, подставить значения 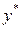 ,
,  ,
,  в исходное уравнение. Из сравнения левой и правой частей найти неизвестные коэффициенты.
в исходное уравнение. Из сравнения левой и правой частей найти неизвестные коэффициенты.
Замечание. Если правая часть 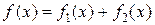 и
и 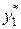 — частное решение уравнения с правой частью
— частное решение уравнения с правой частью 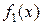 ,
, 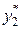 —частное решение уравнения с правой частью
—частное решение уравнения с правой частью 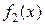 ,то частное решение для уравнения с правой частью
,то частное решение для уравнения с правой частью  будет
будет 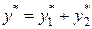 .
.
Пример. Найти общее решение уравнения 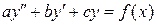 , если
, если 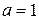 ,
, 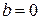 ,
,  ,
,  .
.
Решение. При заданных значениях  уравнение примет вид
уравнение примет вид
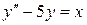 .
.
Обозначим искомое решение через 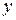 . Тогда
. Тогда 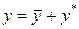 , где
, где 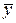 - общее решение уравнения
- общее решение уравнения 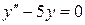 . Составим характеристическое уравнение
. Составим характеристическое уравнение 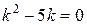 ,
, 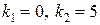 . Следовательно,
. Следовательно, 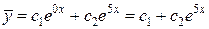 .
.
Найдем 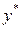 . Так как правая часть уравнения равна
. Так как правая часть уравнения равна 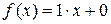 ,то это случай 4 таблицы 4 и частное решение
,то это случай 4 таблицы 4 и частное решение 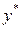 было бы
было бы  ,если бы числа
,если бы числа 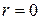 не было среди корней характеристического уравнения. Но так как число
не было среди корней характеристического уравнения. Но так как число 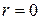 встречается среди корней характеристического уравнения один раз (
встречается среди корней характеристического уравнения один раз ( ), то
), то 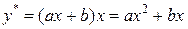 . Найдем
. Найдем 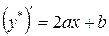 ,
, 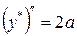 , подставим эти значения в данное уравнение и потребуем, чтобы оно обратилось в тождество
, подставим эти значения в данное уравнение и потребуем, чтобы оно обратилось в тождество
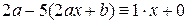 ;
; 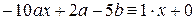 ,
,
откуда 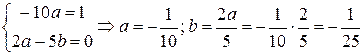 .
.
Таким образом, 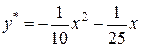 и общее решение уравнения будет
и общее решение уравнения будет  . v
. v
Если в начальный момент времени 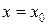 известны
известны 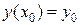 и
и 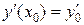 , то можно найти частное решение уравнения, удовлетворяющее этим условиям, т.е. решить так называемую задачу Коши.
, то можно найти частное решение уравнения, удовлетворяющее этим условиям, т.е. решить так называемую задачу Коши.
Пример. Найти частное решение уравнения 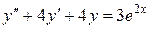 ,удовлетворяющее начальным условиям
,удовлетворяющее начальным условиям  .
.
Решение. Данное уравнение — это уравнение вида 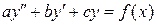 , при
, при 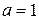 ,
, 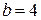 ,
, 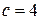 ,
, 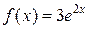 .
.
Найдем сначала общее решение данного уравнения 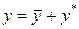 .
.
Для этого решим соответствующее однородное уравнение:
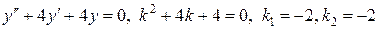 .
.
Следовательно 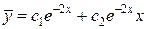 .
.
Так как числа 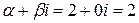 нет среди корней характеристического уравнения, то (случай 3, таблица 2) частное решение
нет среди корней характеристического уравнения, то (случай 3, таблица 2) частное решение 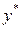 подбираем в таком же виде, как и правая часть
подбираем в таком же виде, как и правая часть 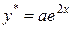 ,
, 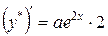 ,
, 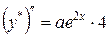 . Подставляем эти значения в уравнение
. Подставляем эти значения в уравнение  .
.
Следовательно, 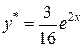 . Значит,
. Значит, 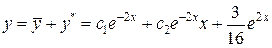 – общее решение данного уравнения. Для нахождения частного решения, удовлетворяющего заданным начальным условиям, найдем:
– общее решение данного уравнения. Для нахождения частного решения, удовлетворяющего заданным начальным условиям, найдем:
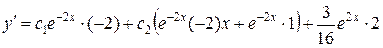 . Так как
. Так как 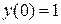 и
и 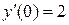 , то получаем
, то получаем

Подставляя эти значения в общее решение, найдем частное решение
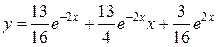 ,
,
удовлетворяющее заданным начальным условиям. v
Пример. Найти частное решение уравнения 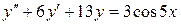 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: 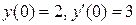 .
.
Решение. Данное уравнение — это уравнение вида 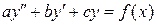 , при
, при 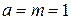 ,
, 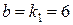 ,
, 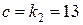 ,
, 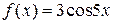 .
.
Решаем уравнение 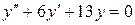 . Составляем характеристическое уравнение
. Составляем характеристическое уравнение 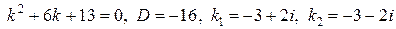 .
.
Следовательно, 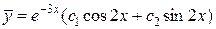 – общее решение уравнения без правой части. По виду правой части
– общее решение уравнения без правой части. По виду правой части 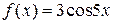 находим число
находим число 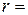
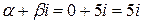 . Такого числа среди корней характеристического уравнения нет, поэтому
. Такого числа среди корней характеристического уравнения нет, поэтому 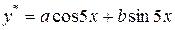 ;
;
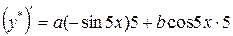 ;
;
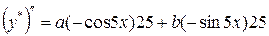 .
.
Подставим эти значения в данное уравнение
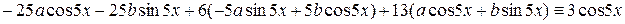 или
или 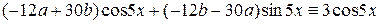 . Сравнивая слагаемые, содержащие
. Сравнивая слагаемые, содержащие 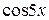 и
и 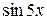 , получим
, получим
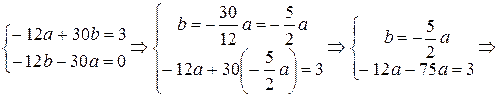
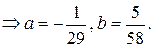
Поэтому
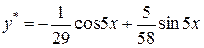 ,
, 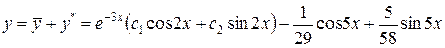 – общее решение данного уравнения. Найдем
– общее решение данного уравнения. Найдем
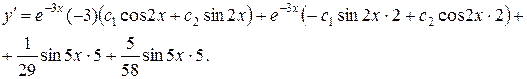
Учитывая начальные условия, найдем: 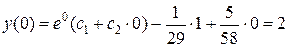 ,
, 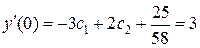 , откуда
, откуда 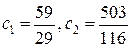 . Подставляя эти значения в общее решение, получим
. Подставляя эти значения в общее решение, получим
 – частное решение исходного уравнения, удовлетворяющее заданным начальным условиям.
– частное решение исходного уравнения, удовлетворяющее заданным начальным условиям.
Физический смысл полученного решения (и предыдущих) в том, что это есть отклонение платформы от положения равновесия в любой момент времени. В частности, при 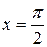 получим
получим
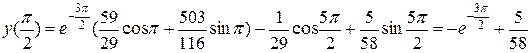 . v
. v
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 493; Нарушение авторских прав?; Мы поможем в написании вашей работы!