
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Степеневі ряди
|
|
|
|
То
Радикальна ознака Коші. Якщо для ряду, загальний член якого, існує
Границя відношення наступного члена до попереднього), то
Ознака Даламбера. Якщо для знакододатного ряду існує
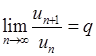 (6.1.5)
(6.1.5)
· якщо 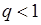 , то ряд збігається;
, то ряд збігається;
· якщо 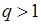 , то ряд розбігається;
, то ряд розбігається;
· якщо 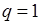 , то про збіжність (розбіжність) ряду нічого сказати не можна (слід скористатися іншими ознаками збіжності рядів).
, то про збіжність (розбіжність) ряду нічого сказати не можна (слід скористатися іншими ознаками збіжності рядів).
Цю ознаку рекомендується використовувати, якщо загальний член досліджуваного ряду містить показникові або факторіальні елементи відносно номера 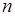 .
.
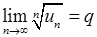 , (6.1.6)
, (6.1.6)
· якщо 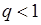 , то ряд збігається;
, то ряд збігається;
· якщо 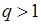 , то ряд розбігається;
, то ряд розбігається;
· якщо 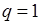 , то про збіжність (розбіжність) ряду нічого сказати не можна (слід скористатися іншими ознаками збіжності рядів).
, то про збіжність (розбіжність) ряду нічого сказати не можна (слід скористатися іншими ознаками збіжності рядів).
Дану ознаку рекомендується застосовувати, якщо загальний член ряду є показниково-степеневою функцією відносно 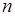 .
.
Інтегральна ознака Коші. Якщо функція 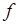 ‑ неперервна, є незростаючою і
‑ неперервна, є незростаючою і 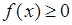 при
при 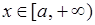 (де
(де 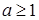 ), то ряд
), то ряд 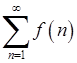 збігається або розбігається одночасно з невласним інтегралом
збігається або розбігається одночасно з невласним інтегралом 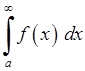 .
.
Умовам цієї ознаки до функції 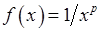 задовольняє узагальнений гармонійний ряд
задовольняє узагальнений гармонійний ряд 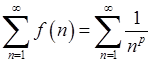 . Через те, що невласний інтеграл
. Через те, що невласний інтеграл 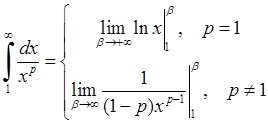 =
=  ,
,
то ряд 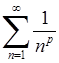 збігається при
збігається при  , і розбігається при
, і розбігається при  .
.
Збіжність знакопереміжних числових рядів  досліджують за ознакою Лейбніца. Якщо
досліджують за ознакою Лейбніца. Якщо
· розпочинаючи з деякого номера, члени ряду, взяті за абсолютним значенням, зменшуються при зростанні їх номера 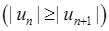 ;
;
·  ,
,
то ряд збігається.
Приклад 6.1.1. Дослідити на збіжність числові ряди: 1) 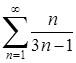 , 2)
, 2) 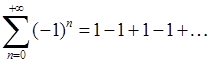 , 3)
, 3)  , 4)
, 4) 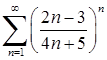 , 5)
, 5) 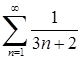 , 6)
, 6)  .
.
Розв’язання. 1) Обчислимо границю загального члена 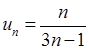 ряду:
ряду:  . Ряд
. Ряд 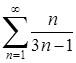 розбігається, бо необхідна умова збіжності (6.1.3) не виконується.
розбігається, бо необхідна умова збіжності (6.1.3) не виконується.
2) Границя загального члена ряду  не існує, тобто необхідна умова збіжності (6.1.3) не виконується. Значить, ряд
не існує, тобто необхідна умова збіжності (6.1.3) не виконується. Значить, ряд  розбігається.
розбігається.
3) Ряд  є знакододатним, бо загальний член ряду
є знакододатним, бо загальний член ряду 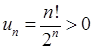 (факторіал
(факторіал 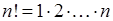 , див. також розділ 8). Наступний член
, див. також розділ 8). Наступний член 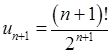 , відношення наступного члена до попереднього
, відношення наступного члена до попереднього 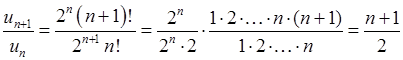 . Тоді границя (6.1.5):
. Тоді границя (6.1.5): 
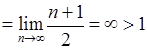 . Отже, ряд розбігається за ознакою Даламбера.
. Отже, ряд розбігається за ознакою Даламбера.
4) Загальний член ряду  . Значить,
. Значить,  , і границя (6.1.6):
, і границя (6.1.6):  . Отже ряд
. Отже ряд 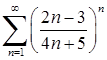 збігається за радикальною ознакою Коші.
збігається за радикальною ознакою Коші.
5) Порівняємо ряд 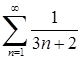 із гармонійним рядом
із гармонійним рядом  .
. 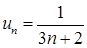 ;
; 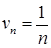 , тоді границя (6.1.4):
, тоді границя (6.1.4): 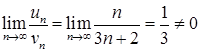 . Отже, за граничною ознакою порівняння досліджуваний ряд розбігається, оскільки гармонійний ряд розбігається за інтегральною ознакою Коші. (Можна було застосувати інтегральну ознаку Коші зразу до вихідного ряду).
. Отже, за граничною ознакою порівняння досліджуваний ряд розбігається, оскільки гармонійний ряд розбігається за інтегральною ознакою Коші. (Можна було застосувати інтегральну ознаку Коші зразу до вихідного ряду).
6) Ряд  є знакопереміжним. Оскільки
є знакопереміжним. Оскільки  ,
,  , то
, то 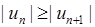 і
і  . Отже, досліджуваний ряд збігається за ознакою Лейбніца.
. Отже, досліджуваний ряд збігається за ознакою Лейбніца.
Література: [1, с. 362 ‑ 376], [2, с. 659 ‑ 673], [4, с. 214 – 246], [15].
Степеневий ряд
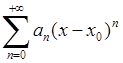 (6.2.1)
(6.2.1)
( ,
, 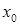 ‑ задані числа) збігається при
‑ задані числа) збігається при 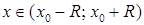 , де
, де 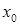 ‑ центр інтервалу (в цій точці ряд набуває вигляду
‑ центр інтервалу (в цій точці ряд набуває вигляду  , отже завжди збігається), а
, отже завжди збігається), а 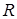 ‑ радіус збіжності
‑ радіус збіжності 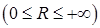 . Для знаходження інтервалу збіжності степеневого ряду можна застосовувати ознаку Даламбера, або радикальну ознаку Коші до знакододатного ряду
. Для знаходження інтервалу збіжності степеневого ряду можна застосовувати ознаку Даламбера, або радикальну ознаку Коші до знакододатного ряду  . Наприклад, застосовуючи ознаку Даламбера до цього ряду, отримаємо умову для визначення інтервалу збіжності степеневого ряду (6.2.1):
. Наприклад, застосовуючи ознаку Даламбера до цього ряду, отримаємо умову для визначення інтервалу збіжності степеневого ряду (6.2.1):
 . (6.2.2)
. (6.2.2)
Розв’язуючи цю нерівність відносно 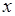 , знаходимо інтервал збіжності
, знаходимо інтервал збіжності  . Множина збіжності або співпадає з цим інтервалом, або є одним із проміжків
. Множина збіжності або співпадає з цим інтервалом, або є одним із проміжків 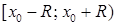 ,
, 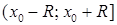 ,
, 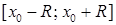 . Якщо степеневий ряд збіжний лише при
. Якщо степеневий ряд збіжний лише при 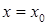 , то його радіус збіжності
, то його радіус збіжності 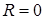 . Якщо ряд збіжний при будь-якому
. Якщо ряд збіжний при будь-якому 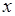 , то
, то 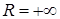 .
.
Степеневі ряди є узагальненням багаточленів і широко застосовуються в науці. Це пов’язано з можливістю представлення багатьох функцій, зокрема всіх елементарних функцій у вигляді сум степеневих рядів, що називаються рядами Тейлора (Маклорена, якщо  ). Наприклад,
). Наприклад,
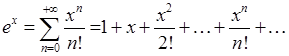 , (6.2.3)
, (6.2.3)
 ,
,  . (6.2.4)
. (6.2.4)
За допомогою розкладу функцій в ряд Тейлора можна з будь-якою точністю обчислити значення функцій, інтегралів, границь і т.д. Саме на цьому грунтуються всі обчислення, що виконуються компьютерами з елементарними та спеціальними функціями.
Приклад 6.2.1. Знайти множину збіжності степеневих рядів: 1)  , 2)
, 2)  , 3)
, 3)  .
.
Розв’язання. 1) Тут 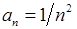 ,
, 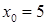 ‑ центр інтервалу збіжності. Оскільки
‑ центр інтервалу збіжності. Оскільки  ,
, 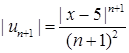 , то (при
, то (при 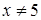 )
) 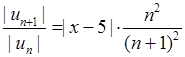 . Значить, за ознакою Даламбера ряд збігається, якщо
. Значить, за ознакою Даламбера ряд збігається, якщо 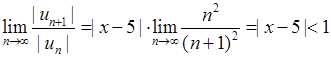 . Тобто, якщо
. Тобто, якщо 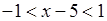 , або
, або 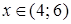 , то степеневий ряд
, то степеневий ряд  збігається. До того ж за ознакою Даламбера якщо
збігається. До того ж за ознакою Даламбера якщо 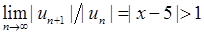 , то ряд розбігається. Залишилось дослідити збіжність ряду на кінцях інтервалу (там, де
, то ряд розбігається. Залишилось дослідити збіжність ряду на кінцях інтервалу (там, де  ).
).
При 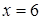 маємо знакододатний ряд
маємо знакододатний ряд  , який збігається за інтегральною ознакою Коші. При
, який збігається за інтегральною ознакою Коші. При 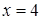 маємо знакопереміжний ряд
маємо знакопереміжний ряд  , який збігається за ознакою Лейбніца. Таким чином, множина збіжності ряду являє собою відрізок
, який збігається за ознакою Лейбніца. Таким чином, множина збіжності ряду являє собою відрізок 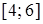 . Тобто ряд
. Тобто ряд 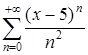 збігається, якщо
збігається, якщо  , і розбігається, якщо
, і розбігається, якщо 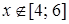 . (Радіус збіжності
. (Радіус збіжності  ).
).
2) Тут  ,
,  . Оскільки
. Оскільки 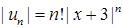 ,
, 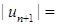
 , то (при
, то (при 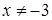 )
) 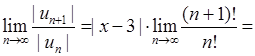
 . Отже, за ознакою Даламбера ряд
. Отже, за ознакою Даламбера ряд  розбігається при всіх
розбігається при всіх 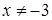 , а збігається лише в точці
, а збігається лише в точці  . (Радіус збіжності
. (Радіус збіжності 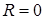 ).
).
3) Тут 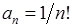 ,
,  . Оскільки
. Оскільки  ,
, 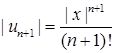 , то (при
, то (при 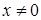 )
) 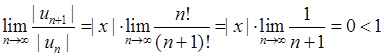 . Отже за ознакою Даламбера ряд
. Отже за ознакою Даламбера ряд  збігається при всіх
збігається при всіх  . (Радіус збіжності
. (Радіус збіжності 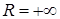 ).
).
Література: [1, с. 377 ‑ 380], [2, с. 626 ‑ 676], [4, с. 247 – 262], [15].
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 1281; Нарушение авторских прав?; Мы поможем в написании вашей работы!