Подвійні, потрійні інтеграли та їх застосування

КРАТНІ, КРИВОЛІНІЙНІ ТА ПОВЕРХНЕВІ ІНТЕГРАЛИ

МОДУЛЬ 5

Основні види простих областей інтегрування на площині:

· Область інтегрування 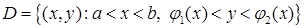є стандартною відносно вісі 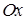. Вона обмежена зліва і справа прямими 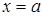і 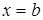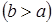, а знизу і зверху – неперервними кривими 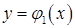і 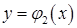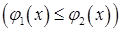, кожна з яких перетинається вертикальною прямою 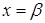(для будь-якого 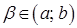), лише в одній точці.

Для такої області подвійний інтеграл обчислюється за формулою:

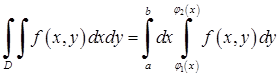, (5.1.1)

причому спочатку обчислюється за змінною 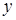“внутрішній” інтеграл 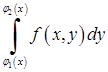, в якому 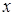вважається сталим.

· Область інтегрування 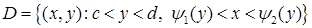є стандартною відносно вісі 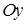. Вона обмежена знизу і зверху прямими 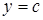і 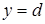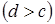, а справа а зліва – відповідно неперервними кривими 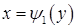і 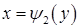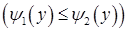, кожна із яких перетинається довільною горизонтальною прямою 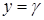(для будь-якого 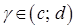) лише в одній точці.

Для такої області подвійний інтеграл обчислюється за формулою:

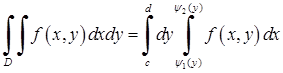, (5.1.2)

причому спочатку обчислюється за змінною 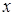“внутрішній” інтеграл 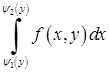, в якому 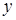вважається сталим.

Праві частини формул (5.1.1), (5.1.2) називаються двократними, або повторними інтегралами. Таким чином, подвійний інтеграл обчислюється за допомогою зведення його до повторного інтеграла. Якщо область не є стандартною, то як часто трапляється, її можна представити у вигляді об’єднання стандартних множин.

Перетворення подвійного інтеграла в прямокутних декартових координатах до інтеграла в полярних координатах 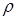, , 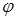які пов’язані з прямокутними координатами співвідношеннями

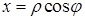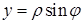, , (5.1.3)

здійснюється за формулою:

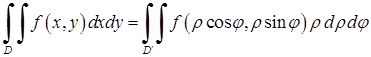. (5.1.4)

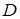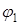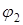
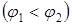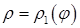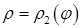
Якщо область обмежена променями, які утворюють з полярною віссю кути і , і кривими і , то відповідні полярні координати змінюються в межах області 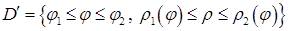, і тоді

. (5.1.5)

Приклад 5.1.1. Обчислити інтеграл 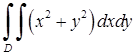, де 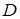‑ чверть круга 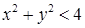, що лежить в першій координатній чверті .

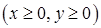Розв’язання. У відповідності з формулами (5.1.4), (5.1.5):

.

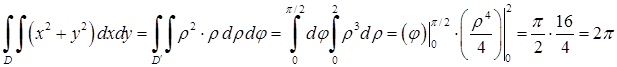Площа плоскої фігури 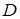виражається формулою

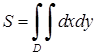. (5.1.6)

Об’єм циліндричного тіла (обмеженого зверху неперервною поверхнею 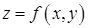, знизу – площиною 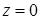і з боків – циліндричною поверхнею з твірними, паралельними осі 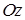), що вирізає на площині 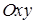область 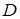, обчислюється за формулою:

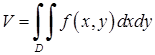. (5.1.7)

Якщо пластинка займає область 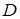площини 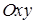і має змінну поверхневу густину 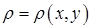, то маса пластинки виражається подвійним інтегралом

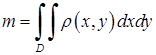. (5.1.8)

Координати центра мас обчислюються за формулами:

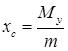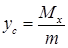, , (5.1.9)

де , .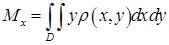

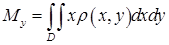Якщо область інтегрування 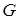визначається нерівностями 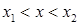, , 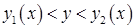, 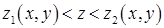де 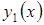, , 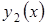, 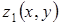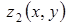– неперервні функції, то потрійний інтеграл від функції 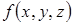по області 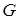, обчислюється за формулою:

. (5.1.10)

Об’єм просторового тіла, що займає область 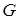, визначається за формулою:

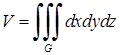. (5.1.11)

Якщо 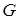– деяка область простору, яку займає матеріальне тіло з густиною 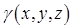, то маса тіла 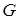визначається формулою:

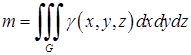. (5.1.12)

Приклад 5.1.2. Для фігури 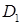, що обмежена лініями, вказаними в прикладі 3.3.1: а) записати подвійний інтеграл ( 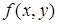‑ неперервна функція в 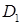) у вигляді повторного інтеграла та змінити порядок інтегрування; б) знайти масу пластини 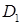, якщо густина маси 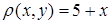; в) обчислити об’єм циліндричного тіла 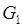, обмеженого зверху площиною 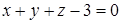, знизу – площиною 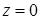і з боків – прямою циліндричною поверхнею, що вирізає на площині 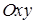область 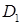; г) знайти масу циліндричного тіла 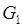, якщо густина маси .

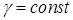Розв’язання. а) Криволінійна трапеція 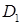(див. рис. 3.3.1) обмежена зверху – параболою 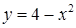, знизу ‑ віссю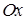 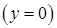та проектується на відрізок осі 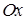. Значить, 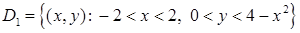є стандартною відносно вісі .

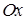З іншого боку, 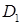обмежена зліва – віткою параболи 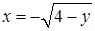, справа – віткою параболи 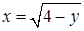та проектується на відрізок 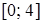осі 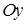. Таким чином, 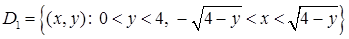є стандартною відносно вісі .

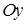Отже, запишемо подвійний інтеграл у вигляді обох повторних за формулами (5.1.1), (5.1.2):

.

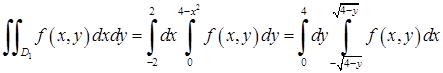б) Знайдемо масу пластини 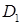за формулою (5.1.8) (де густина маси 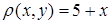): 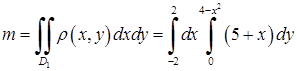. Спочатку обчислимо за змінною 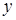“внутрішній” інтеграл, в якому 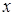вважається сталим:

.

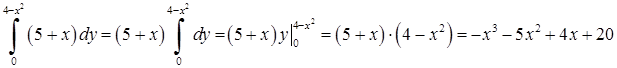Тоді .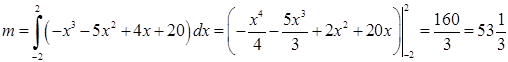

в) Об’єм циліндричного тіла (обмеженого зверху площиною 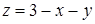) згідно (5.1.7): 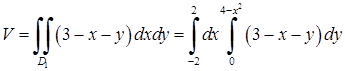. “Внутрішній” інтеграл

.

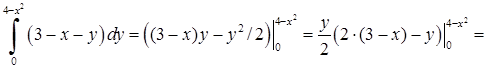
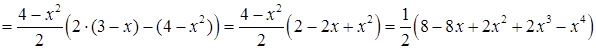Значить, 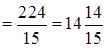(куб. од.)

г) Знайдемо масу циліндричного тіла за формулою (5.1.12):

.

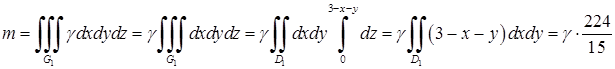Зауважимо, що приклад 5.1.2 відповідає завданню 5.1 контрольної роботи.

Література: [1, с. 470 ‑ 492], [2, с. 581 ‑ 616], [3, с. 494 – 499], [13].

Дата добавления: 2014-12-17