Третье началоКТД известно как теорема Нернста [77,78], следствием которой является так называемый принцип недостижимости нуля абсолютной темпе­ратуры. 1 страница

Всякое тело продолжает удерживаться в состоя­нии покоя, равномерного кругового или равномерного прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

При этом необходимо помнить о том, что любая физическая теория, основанная на принципах покоя, равномерного кругового, либо равномерного прямо­линейного движения (т.е. не учитывающая взаимо­действия тел с окружающей средой), обречена на провал.

Подводя итоги изложенного, особенно важно отме­тить, что проведенный анализ выявил существование равенства (3.34), находящегося в явных формальных противоречиях со вторым и третьим законами классической механики, не содержащими параметра g.

3.3. Гравитационная деформация тел

В статической аксиоматике Евклидова пространства, все области последнего обладают одинаковой мерно­стью, и перенос измерительного инструмента (напри­мер, жесткого метра) из одной области пространства в другую по определению не изменяет его геометрических размеров. Эта математическая аксиоматика привнесена без изме­нений в механику Ньютона и использована для описа­ния взаимодействия тел в гравитационном поле. Такой подход неявно постулирует изотропность пространства, отсутствие воздействия внешнего гравитационного поля на находящиеся в нем тела, а, следовательно, и отсутст­вие влияния напряженности внешнего гравиполя на па­раметры тела. Таким образом, в классической механике постулируется, что тело при перемещении во внешнем гравиполе не испытывает воздействия со стороны по­следнего и не деформирует, т.е. остается тождественным самому себе. Поэтому как система тело либо не взаимо­действует с внешним гравиполем, либо это взаимодей­ствие не является физическим. Оставим последнее предположение без внимания как не имеющее отноше­ния к физике. Рассмотрим притяжение тел как следствие взаимодействия между системами свойств притягиваемых тел.

Надо отметить, что механика Ньютона отождествляет тело с гравитирующей точкой и потому все описание притяжения между телами проводится как взаимодейст­вие гравитирующих центров — точек. Поскольку гравитирующие центры — абстракция, а точка — геометриче­ская фигура, не имеющая объема и не обладающая физическими свойствами, то и никаких деформаций с ней происходить не может.

Однако тела — не точки. Они, как системы, образуют свое пространство, поверхность которого связана как со свойствами самого тела, так и со свойствами внешнего пространства. И если в системе тела или во внешнем пространстве происходит изменение количественной величины некоторых свойств (например, напряженности внешнего гравиполя), то эти изменения должны отра­жаться и на величинах свойств самого тела. В частности, следует ожидать деформации геометрических парамет­ров (объема) тела. Это обстоятельство является важ­нейшим для понимания сущности гравитационного взаимодействия.

Гравитирующие тела достаточно условно можно пола­гать точками только тогда, когда напряженность грави­поля в их нейтральной зоне на три-четыре порядка меньше, чем на поверхности. Во всех остальных случаях рассмотрения гравитационного взаимодействия отсчет расстояния между телами производится не от их цен­тров, а от поверхности. Именно такой подход к описа­нию гравитационного взаимодействия проводится в рус­ской механике. И именно он приводит к пониманию сущности гравитационной деформации тел. Рассмотрим его.

Тело, находящееся в пространстве над поверхностью, взаимодействует с внешним гравиполем и потому при­тягивается Землей. В этом взаимодействии участвуют все свойства тел, однако в закон притяжения входят только массы тела и Земли, расстояние между телами, гравитационная «постоянная» и сила притяжения между ними. Особо подчеркну то обстоятельство, что само притягиваемое тело в законе представлено только «не­изменной» массой. Другие свойства данного тела в по­следующих расчетах явно не участвуют ни во взаимо­связи, ни по отдельности.

Можно предложить множество экспериментов, под­тверждающих наличие гравидеформации тел при изме­нении напряженности внешнего гравиполя. Некоторые из них, связанные с перемещением мерного инструмента по высоте над поверхностью, уже приводились ранее. Как отмечалось, измерительные инструменты из раз­личных материалов, отрихтованные на мерной миле в долине и перенесенные на такую же милю на плато, бу­дут давать различное значение ее длины. Данное разли­чие является следствием того, что внутреннее строение, химический состав тела и его свойства влияют на харак­тер деформации при изменении напряженности внешне­го гравиполя. А это означает, что гравидеформация вы­зывает изменение не только линейных параметров тел, но и их массы и веса при статическом изменении поло­жения тела по высоте, а при динамическом — различные ускорения при падении. В последнем случае сопротив­ление внутренних сил тела грависжатию вызывает возникновение внешних тормозящих воздействий, обу­словливающих различное ускорение «свободно» падаю­щих тел.

Можно проделать более простой эксперимент. Доста­точно уравновесить на рычажных весах с разрешающей способностью ~10^-7 два тела из различных материалов (например, вода и свинец) на одной высоте и, подняв их на высоту 1 км, убедиться, что достигнутое равновесие на высоте нарушается больше, чем это следует из классической механики. Не корректируя показания весов, опустить их вместе с грузами на прежний уровень и по­лучить начальное равновесие рычагов. Это и будет сви­детельством изменения веса тел по высоте.

Эти достаточно простые и относительно дешевые экс­перименты не проводились не из-за технологических сложностей, а потому, что противоречили постулату изотропности пространства и принципу эквивалентности. Согласно последнему, по К. Уиллу, «все тела в гра­витационном поле падают с одним и тем же ускорением вне зависимости от их массы или внутреннего строения» [11].

В конце 1986 г. группа физиков во главе с Э. Фишбахом опубликовала в журнале Phys.Rev.Letters гипотезу о возможном падении тел в вакууме с различным ускоре­нием. Гипотеза противоречила основам классической механики (все тела, независимо от своих свойств, пада­ют в вакууме с одинаковым ускорением) и опиралась на ряд экспериментов группы австралийских геофизиков во главе с Ф. Стейси по измерению значения гравитацион­ной «постоянной» G в глубоких шахтах. При опускании приборов в них фиксируется постоянное возрастание силы притяжения. Аналогичный результат, был получен при опускании гравиметров в полуторакилометровую скважину, пробуренную во льдах Гренландии, и при подъеме на 600 метровую телевизионную башню в шта­те Северная Каролина. Более того, проведя тщательный анализ результатов классических эксперимен-тов Г. Этвеша, группа Фишбаха обнаружила в них подтвержде­ние своей гипотезы. Таким образом, гипотеза имела дос­таточно доказательное обоснование и претендовала стать настоящей научной сенсацией.

Объясняя эти эксперименты, Фишбах выдвинул пред­положение о существовании в природе пятой силы — си­лы отталкивания, с радиусом действия в несколько сот метров и примерно на два порядка более слабой, чем сила гравитационного притяжения. Предполагалось, что величина пятой силы не зависит от массы, а определяется общим барионным числом на единицу массы (обусловливается чис­лом протонов и нейтронов в теле). Основой существова­ния сил отталкивания между одинаковыми телами разного химического состава становится отсутствие пропорциональности между барионным зарядом и мас­сой тел.

Гипотеза вызвала широкую дискуссию по проблеме пятой силы и стремление эмпирического доказательства ее существования. В течение ряда лет было проведено несколько десятков экспериментов по проверке гипоте­зы и предложены различные физические обоснования возможности существования этой силы. Тем не менее, однозначного доказательства реальности пятой силы получено не было. Часть экспериментов подтверждала наличие такой силы, но большая часть ей противоречи­ла.

Международный симпозиум, состоявшийся в августе 1988 г. в Австралии по проблеме пятой силы и выработке теоретического и экспериментального, подхода к это­му явлению оказался безрезультатным и ограничился рекомендацией о необходимости дальнейшего изучения данного явления. Отсутствие однозначного эмпирического доказательства существования пятой силы приту­шило интерес к данной проблеме, и к настоящему вре­мени упоминания о ней появляются в научных публика­циях от случая к случаю. Тем не менее, проблема остается. Чем же она вызвана?

Как известно, ньютоновская механика не предполагает изменения количественной величины свойств тела, на­ходящегося в гравитационном поле, в результате изме­нения напряженности этого поля. Следовательно, тела лежащие на поверхности Земли, остаются тождествен­ными самим себе и при подъеме их на некоторую высо­ту над поверхностью. Тождественность тел при переме­щении в гравитационном поле обусловливает постоян­ство ускорения при их падении в вакууме (в эфире).

Постулирование тождественности тел с изменением внешнего гравитационного поля физически означает, что гравиполе данных тел не взаимодействует с внеш­ним гравиполем, и поэтому становятся необъяснимыми как причины, вызывающие их падение, так и «переливы» потенциальной и кинетической энергий с изменением высоты.

Тем не менее, тело, находящееся на поверхности, сво­им гравитационным полем взаимодействует с гравипо­лем Земли и только поэтому притягивается ею. По­скольку внешние и внутренние свойства тела взаимосвя­заны, то изменение любого из них вызывает соответ­ствующее явное или неявное изменение всех остальных свойств (например, напряженности собственного грави­поля, массы, геометрических размеров и т.д.) [5].

Поэтому при движении тела вверх или вниз относи­тельно поверхности явственно изменяется величина двух параметров: напряженность внешнего гравиполя g и расстояние R между центрами масс тел. А так как на­пряженность гравиполя тела g₁, связана с напряженно­стью внешнего гравиполя g₀, то изменение последнего должно вызывать соответствующее изменение напря­женности гравиполя тела, а вместе с ним и всех осталь­ных свойств. Поскольку произведение напряженности гравиполя g ₁ на квадрат радиуса r есть инвариант, то из­менение напряженности гравиполя тела при подъеме вызывает пропорциональное изменение его геометриче­ских параметров. То есть, изменение напряженности внешнего гравиполя сопровождается гравита-ционной деформацией тела. А это главное для понимания и объ­яснения гравитационных взаимодействий.

Рассмотрим пример [44]:

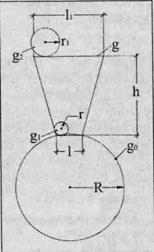
Рис. 24.

Предположим, что на поверх­ности по отвесу возведена баш­ня высотой h = R (где R – ради­ус Земли) и длиной основания l, а верхней площадки l₁ (рис.24). На полу башни лежит тело – шар, радиусом r. Поднимем этот шар на верхнюю площадку и определим его радиус. По­верхностная напряженность гравиполя тела на полу g₁ гра­виполя Земли g_о. Напряжен­ность гравиполя тела на верх­ней площадке g₂, Земли g. Если в системе тело-Земля на­пряженность внешнего грави­поля g_о пропорциональна напряженности гравиполя тела g₁ то с подъемом шара на площадку напряженность по­верхности его гравиполя меняется пропорционально на­пряженности гравиполя Земли, а вместе с ней меняется и радиус сферы r₁. Зависимость напряженностей опре­деляется уравнением:

g₁/g_o = g₂/g. (3.35)

Напряженность внешнего гравиполя g на верхней площадке башни находим из уравнения:

g = A/ (h + R) ² = g_о/ 4, A = R²g_о. (3.36)

Подставляем в уравнение (3.36) значение g из (3.35) и находим g_2:

g₂ = g₁/ 4. (3.37)

Напряженность гравиполя сферы связана с радиусом инвариантом g₁r² = const, и количественная величина инварианта не изменяется с подъемом тела на верхнюю площадку. Поэтому имеем:

g₁r² = g₂r₁² (3.38)

Подставляя в (3.38) значение g₂ из (3.37), получаем ве­личину радиуса шара r₁ поднятого на верхнюю площад­ку башни:

r₁ = 2 r. (3.39)

Равенство (3.39) показывает, что с подъемом тела (сферы) на высоту его геометрические размеры возрас­тают пропорционально изменению напряженности на­ружного гравиполя, а физические параметры остаются постоянными. Физический жесткий метр на полу башни отло­жится столько же раз, сколько и на верхней площадке. Поэтому длина стороны пола башни l физически равна длине стороны верхней площадки l₁:

l = l₁ – физически,

а геометрические размеры их различны и l ≠ l₁:

l =1/2 l.

Все тела, как и жесткие измерительные стержни, с возрастанием напряженности внешнего гравиполя «гео­метрически» сжимаются (деформируют), а при уменьшении – расширя­ются. (Это и есть гравитационный аналог температурно­го эффекта, описанного А. Пуанкаре.) Геометрические размеры тел определяются их местом во внешнем грави­тационном поле. Изменение геометрических размеров и есть гравитационная деформация тела. Последняя оп­ределяет количественную величину взаимоперехода по­тенциальной и кинетической энергии при подъеме или опускании тела во внешнем гравиполе. Именно гравита­ционная деформация обуславливает режим «свободно­го» падения тел в эфире.

Рассмотрим, учитывая гравитационную деформацию тел, результаты некоторых экспериментов, необъясни­мых с позиций ньютоновской механики. Их можно достаточно условно разделить на две группы: эксперимен­ты в статической и динамической постановке. Еще раз отмечу, что и классическая механика, и теория от­носительности, и другие гравитационные гипотезы по­стулируют тождественный характер поведения тел приэтих качественно разных взаимодействиях.

Различие статической и динамической природы грави­тационных взаимодействий обусловлено дихотомией понятия «ускорение свободного падения» g. С одной стороны, оно является именно ускорением тел в падении (в динамике), с другой — выполняет функции напряжен­ности гравиполей тел (в статике). Поэтому при статиче­ской постановке эксперимента более сказывается уча­стие во взаимодействии свойств, связанных со сжимаемостью тел в условиях, когда время и скорость сжатия не существенны. И потому состояние поднятых (опущенных) относительно своего первоначального по­ложения тел определяется изменением плотности ρ и сжимаемости х.

При «свободном» падении тел в возрастающем внешнем гравитационном поле (динамическое взаимодействие) сопротив-ление сжатию обусловливает движение их с различным ускорением. В свою очередь и скорость гравитационного сжатия в падении и величина де­формации определяются физическими и химическими свойствами тел.

Для определения деформации поднимаемых (опускае­мых) над поверхностью Земли тел можно предложить расчетную формулу, выведенную Д.В. Черняевым [43]:

∆ z = 9 h² (l/ x₂ρ₂ – 1/ x₁ρ₁)/ gR², (3.40)

где ∆ z – расчетное расстояние между телами, брошен­ными с высоты h, g – напряженность гравитационного поля (ускорение свободного падения), R – радиус Земли, ρ₁, ρ₂ – плотности опущенных тел, ѕ₁,ѕ₂ – коэффициенты сжимаемости опущенных тел.

Формула (3.40) позволяет определить расстояние z между двумя как бы одновременно опущенными телами после опускания их с высоты h = 1 км и в пересчете этой разницы на собственный вес тела на новой высоте. Рас­чет по (3.40) производился для 6 типов материалов, имеющих одинаковый первоначальный вес, равный Р = 2,13865∙10⁴ г, и, как видно из табл. 8, на новой высоте все тела имеют уже различный вес. По закону Ньютона вес всех опущенных с одной высоты тел должен оста­ваться одинаковым и равным 2,14032113∙10⁴ г.

Таблица 8
Материалы Х, 10^-12 ρ, г/см³ Р_п, 10⁴ г

смс/г

1 Стекло 1,3 2,6 2,14048928

2 Сталь 0,6 7,7 2,14048913

3 Медь 0,7 8,93 2,14048902

4 Свинец 2,3 11,34 2,14048879

5 Платина 0,36 21,4 2,14048896

6 Уран 1,8 19,05 2,14048877

Коэффициенты сжимаемости Х достаточно приблизи­тельны, поскольку свойство сжимаемости тел для одно­го и того же материала варьируется в широких пределах (до порядка) в зависимости от технологии получения образца, его химической чистоты, кристаллической структуры и т.д. А поэтому при подготовке подобных тел к эксперименту необходимо фиксировать параметры каждого образца на высоте проведения эксперимента.

В статической постановке проводились эксперименты Р. Этвеша, Дж. Эйри, С. Стабса, Э. Адельберга, П. Бойнтона, П. Тибергера и большинство других. В этих экспериментах отсутствуют свободно падающие тела и используются различные конструкции крутиль­ных весов или гравиметров.

Наиболее известен в статической постановке классический эксперимент Р. Этвеша, проведенный более 80 лет назад. Попытка двух исследовательских групп Бойнтона, а также Стабса и Адельберга повторить экспери­менты Этвеша с применением пробных тел из других материалов не привели к получению аналогичных ре­зультатов.

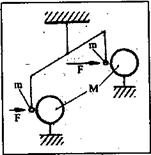
В эксперименте Этвеш использовал крутильные весы, подвешенные на упругой нити (рис. 25). На коромысле весов закреплялись одинаковые по массе m пары пробных тел из различных материалов (всего 13 пар), поме­щаемые в эксперименте с одной стороны от массивных тел М. Если сила притяжения пробных тел к массивным будет неодинакова, то коромысло повернется на некоторый угол и приборы зафиксируют этот поворот [5]. Результаты эксперимента, проделанного с точностью до 10^-9-10^-10, были интерпретированы Этвешем в отчете как доказательство того, что ускорение свободного па­дения для любых тел с данной точ­ностью постоянно. Однако по отчету в 9-м знаке обнаруживаются заметные статические различия в ускорении 10 пар пробных тел. Именно эти различия и использовал

Рис. 25

Фишбах для подтверждения своей гипотезы. Поскольку в экспериментах Этвеша фигурирует не ускорение свободного падения, а изменение собственной напряженности гравитационного поля пробных тел, то анализ, результатов Эксперимента надо начинать с выяс­нения ответа на вопрос: на одном ли уровне проводилось вывешивание пробных тел и эксперимент с ними? К сожалению, это важнейшее условие для корректного объяснения эксперимента не зафиксировано ни в отчете Эт­веша, ни в публикациях Стабса, Адельберга, Бойнтона и ни в каких других публикациях, И это не удивительно, поскольку, как уже говорилось, механика Ньютона не предполагает никаких изменений в напряженности под­нимаемого или опускаемого тела.

А потому, проводя статические гравитационные опы­ты, экспериментаторы очень тщательно готовят и выве­шивают образцы, проводят и регулируют измеритель­ную аппаратуру, продумывают и отсеивают возможные помехи, но, по-видимому, не обращают внимание на то, на какой высоте относительно поверхности Земли гото­вятся образцы и на какой проводится эксперимент. И если высота подготовки пробных тел отличается от вы­соты, на которой эксперимент с этими телами проводит­ся более чем на 10 м, то получаемые уже в 9-м знаке ре­зультаты очень сложно интерпретировать на основе ньютоновской механики.

Результаты, полученные в эксперименте Этвешем, по­казывают, что большинство пробных тел из твердых ма­териалов вывешивались на несколько десятков метров выше (ниже?) уровня проведения эксперимента, вероят­но, в некоторой мастерской. А три пары тел из мягких материалов вывешивались в другом месте, скорее всего в лаборатории, где проводился эксперимент. Результаты от этих трех пар противоречили гипотезе Фишбаха и по­тому им не рассматривались. И получилось, что, прове­дя вывешивание пробных тел в мастерской, Этвеш привел напряженности их гравиполей к одной и тoй же величине относительно гравиполя Земли в данном месте.

Подъем (опускание?) тел к месту проведения экспе­римента сопровождались изменением напряженности гравиполей тел. Это и повлекло за собой последующее отличие их во взаимодействии с массами М на один, два последних знака. Для трех пар тел, вывешиваемых на месте эксперимента, такого отличия уже не наблюда­лось.

Группа П. Тибергера из Национальной физической ла­боратории (Брукхейвен США) использовала в экспери­менте полую медную

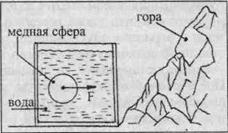
Рис. 26

сферу с удельным весом, равным удельному весу воды, и плавающую в ней вблизи горы (рис.26). По-видимому, изготовление сферы и вывеши­вание ее в воде производилось в некотором месте, в уда­лении от горы. И пе­ремещение готовой сферы, а, возможно, и воды, в гору со­провождалось рассо­гласованием напряженностей их собст­венных гравиполей.

Поэтому медная сфера под действием сил F притяжении горы двигалась к ней, как бы подтверждая гипотезу Фишбаха. Исследуя изменения напряженности грави­тационного поля g в глубоких шахтах Австралии, Дж. Эйри регистрировал систематическое завышение эмпи­рической величины гравитационой «постоянной» G от­носительно ее официального значения [61]. Величина гравитационной постоянной в шахтах составляет G_ф = 6,672∙10^-11(±0,024) м³кг^-1с^-2, тогда как ее значение, при­нятое международной комиссией по фундаментальным константам., равно G = 6,67259∙10^-11 (±0,00085) м³кг^-1с^-2 и, следовательно, с опусканием в шахты сила притяже­ния возрастает, что согласуется с экспериментом Тибергера и как бы соответствует гипотезе Фишбаха.

Зная стандартное значение G, можно, используя фор­мулу (2.49), найти среднюю глубину R,p, на которую опускались приборы в шахты:

G²/R = (6,6725910^-8)²/6,378∙10⁸ = 6,98079∙10^-24 = А.

Подставляем фактическое G_ф и получаем:

R_ф = G² /A = 6,3769 км.

Откуда средняя глубина шахт равна:

R – R_ф = 1,1 км.

Группа ученых под руководством К. Стабса и Э. Адельберга поместили установку типа Этвеша (крутильные весы) с пробными телами из меда и бериллия у склона горы и не получили подтверждения существова­ния пятой силы. (Можно предположить, что материалы готовились на одной высоте с местом проведения экспе­римента или, что также вероятно, совокупность свойств меди и бериллия обусловливает им одинаковую количе­ственную величину деформации.)

Теперь остановимся на динамических экспериментах. По постановке эксперименты с падающими телами сложнее статических, диапазон варьирования ими скуд­нее и потому проводятся они реже. Но именно в этих экспериментах можно наблюдать за изменением ускоре­ния свободного падения.

Если в падении происходит меха­ническая деформация тела, а, следовательно, скорость сжатия не может превосходить скорость звука в теле, то можно получить следующую качественную формулу для максимального изменения расстояния ∆z между од­новременно отпущенными и «свободно» падающими с высоты h телами:

∆z = h² [(c₁² – c₂²)/ R²]/g, (3.41)

где с₁ и с₂ – скорость звука в падающих телах. В табл. 8 показано расчетное изменение расстояния по отношению к стали между одновременно отпущенными телами — шарами одного радиуса и относительное уско­рение: ∆а = (g_c – g_t) /g при падении их с высоты 1 м. Из нее следует, что все пробные тела за один и тот же про­межуток времени должны проходить участки пути раз­личной длины и, следовательно, падать с неодинаковым ускорением. Причем быстрее всех будет падать тело из стали, а медленнее всех — свинцовое тело.

Таблица 8

	Материалы	с 10^5 см/с	∆z 10^-6см	∆а 10^-8
	Стекло	5,00	0,4	4,0
	Сталь	1,159	–	–
	Медь	3,066	3,3	3,3
	Свинец	1,350	6,2	6,2
	Платина	2,688	4,9	4,2
	Уран	2,010	5,7	5,7

В классической постановке эксперимент с падающими в вакууммированной камере телами был проведен груп­пой Дж. Фаллера в Колорадском университете [61]. С помощью интерферометра определялось ускорение сво­бодного падения пробных тел, изготовленных из меди Сu и урана U. Луч света от лазера 1расщеплялся полупрозрачным зеркалом 2 на два луча 3, по­следние, попадая на призмы 4, укрепленные на падающих телах 5 и преломляясь ими, направля­ются в интерферометр 6. Если тела падают с различным уско­рением, то интерференционные полосы от световых лучей в интерферометре испытают относи­тельное смещение (рис. 27).

По гипотезе Фишбаха, урано­вое тело должно было падать с большим ускорением, 10^-9, чем медное. Однако эксперименты показали, что медное тело падает быстрее уранового с относительным ускорением (a₂ – a₁)/ g = 5∙10^-10, что проти­воречит результатам Этвеша, но оказывается достаточно близко к расчетной величине, найденной по формуле (3.41) и равной ~10^-9. Возможно, эта близость — следст­вие достоверности результатов экспериментов, а отсут­ствие равенства 10^-9 ≠ 10^-10 может вызываться следую­щими причинами:

• различием в свойствах используемых тел,

• различием в параметрах опытных образцов,

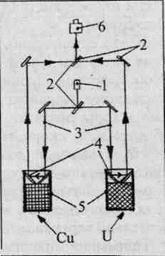
• сглаживающим воздействием стабилизирующей ап­паратуры и т.д.

Рис. 27.

Сиэтлская группа П. Бойнтона использовала смешан­ную статико-динамическую модель гравитационного воздействия на пробное тело. Вместо крутильных весов они использовали кольцо, одна половина которого была сделана из алюминия, а другая из бериллия. Закрутив кольцо, и, таким образом, заменив статические гравивоздействия на движение вращения, они исследовали динамику вращающе-гося мaятникa. И обнаружили, про­водя эксперимент вблизи отвесной скалы, что «пo виду колебаний кольца можно судить о различном статиче­ском взаимодействии массы скалы с каждой из половин маятника».

И это естественно. Сжимаемость алюминия и берил­лия различна. Когда кольцо поворачивалось к горе од­ной стороной, например алюминием, оно сжималось медленнее и происходило торможение вращения. Когда же у горы двигался бериллий, это сжатие было более быстрым, и скорость кольца относительно движения берилия возрастала. Эксперимент требует высокой точности наблюдения и правильной интерпретации. Результат можно значительно улучшить, заменив кольцо гантелью из тех же материалов и фикси­руя одновременно с вращением колебание подвеса отно­сительно вертикали.

Примерно аналогичный по конструкции установки эксперимент, переводящий статическое воздействие внешнего гравиполя во вращательное движение пробно­го тела, а потому и более эффективный, проводился в России Б.Н. Додоновым [44]. Использовалась следую­щая схема эксперимента: В круглой металлической пли­те 1, прямоугольного сечения имеется отверстие 2, в котором может размещаться кольцо 3 из пробного материала. В плите прорезаются пазы 4, направленные по касательной к кольцу 3. Пазы изменяют перпендику­лярное воздействие сжимающего гравитационного поля сплошной плиты на касательное сжатие совокупностью образовавшихся отдельных плит. Если кольцо 3пове­сить горизонтально на нити 5 и, дав ему успокоиться, надвинуть без соприкосновения отверстием плиту 1 (по­казано на рис.28 штрихами), то касательное сжатие кольца гравиполями плит, вызовет его вращение в на­правлении, противоположном сжатию. Под этим воз­действием кольцо совершает до двух и более оборотов.

Дата добавления: 2014-11-29