Взаимодействие тел в эфир­ном пространстве обусловливает им равное и про­тивоположное противодействие. 3 страница

Таким образом, измененный эксперимент Саньяка не просто зафиксирует возможность определения состоя­ния наружного диска приборами, находящимися внутри него, но и позволит однозначно выяснить, какая из реля­тивистских теорий (Г. Лорентца или А. Эйнштейна) бо­лее адекватно отражает природные процессы.

Известно, что фотоны света, движущиеся от гравитирующего тела, уменьшают частоту волны — так назы­ваемое красное смещение, и наоборот, — движущиеся к гравитирующему телу фотоны увеличивают свою часто­ту, т.е. испытывают фиолетовое смещение. Это свойство фотонов можно использовать для доказательства появ­ления локального гравитационного поля внутри полого, вращающегося диска, заменив систему зеркал Саньяка источником света и его приемником на ободе или на оси.

Естественно, что, обладая направленной системой мышления и пройдя школу механицизма и теории отно­сительности, ученые не могли предвидеть возможности проведения таких экспериментов, но могли наткнуться на них случайно. Именно такая случайность произошла с группой английских исследователей, проводивших эксперименты по подтверждению теории относительно­сти [126]. То, что произошло в результате, хорошо опи­сано у В.Н. Демиденко [127]:

«... В 1961 г. Чампни и Мун решили подтвердить по­перечный эффект Доплера с помощью нового метода — эффекта Месбауэра. Они расположили приемник и ис­точник фотонов на противоположных концах диаметра ротора (рис. 76, а). В роторе было просверлено сквозное отверстие, где фотоны могли бы путешествовать.

Так как источник двигался относительно приемника под прямым углом, то по теории относительности здесь должен был бы наблюдаться поперечный эффект — красное смещение — уменьшение частоты волны. Одна­ко эффект оказался нулевым.

Американские физики Хей, Шиффер, Креншоу, Эгелфаст решили выяснить, а что будет, если источник по­местить в центре ротора? Появился эффект, истолко­ванный как красное смещение (1962 г.). Кондиг повышает точность эксперимента и обнаруживает странное расползание резонансной линии, но сам эф­фект опять считается красным смещением.

Рис. 76, а-в

Наконец годом позже (в 1969 году) Чампни, Иссаак и Кан произвели предварительный сдвиг резонансных ли­ний. Для этого они нанесли источник гамма квантов — радиоактивные атомы железа на пластинчатую основу — мягкую медь и вновь замерили эффект. Источник был в центре ротора (рис. 76, б). Когда ротор привели во вра­щение, то неожиданно для экспериментаторов резо­нансная линия поползла в сторону фиолетового смещения. Резонансные линии источника и приемника совме­стились, а затем разошлись. Сомнений быть не могло. Наблюдался не красный, а фиолетовый сдвиг. Результат был настолько ошеломляющим, что заметка о нем была предельно краткой. Никаких выводов не делалось (кур­сив мой – А.Ч.), а приводились лишь данные экспери­ментов».

Ничего удивительного: искали подтверждение теории относительности, а получили подтверждение существо­вания эфира (в период, когда он однозначно отсутст­вовал по постулату), выраженное в форме локализации гравитационного поля. И хотя исследователи не исклю­чали возможности существования эфира, в этой кон­кретной постановке эксперимента его наличие не пред­полагалось. И снова мировоззрение, вслед за Саньяком, помешало сделать открытие локализации гравиполя. Кстати, анализируя эффект группы Чампни, некоторые ученые несколько позднее предположили, что в данном случае имеет место локализация гравиполя [128]. Но к ним не прислушались.

Занимаясь изучением экспериментов с прохождением лучей света во вращающемся полом диске, В.И. Деми­денко в следующей работе [129] нашел объяснение опы­там английской группы исследователей: «... Пусть на окружности вращающегося ротора находится приемник. Фотон налетает на него, в результате чего импульс фо­тона относительно приемника увеличивается, происхо­дит векторное сложение двух импульсов. Обнаружива­ется фиолетовый сдвиг частоты. Если же вращается источник, то масса виртуального фотона, который мо­жет быть испущен, находится в движении, обладая на­чальным импульсом. В процессе излучения этот им­пульс векторно отнимается от квантового импульса фотона (импульс излучения), и в результате приемник, находящийся в центре ротора, регистрирует уменьшение энергии и частоты приходящих фотонов — красное смещение (рис. 76, в) ».

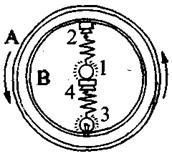
Это объяснение может считаться подтверждением теории относительности. Но, рассматривая источник и приемник фотонов в движении с ротором, В. Демиденко упустил вариант, по которому и источник и приемник могут быть неподвижными, а ротор вращающимся. В этом случае ударное увеличение и уменьшение импуль­са фотона будет отсутствовать, а красное или фиолето­вое смещение останется. Что тогда? Ведь эта постановка эксперимента не предусматривается ОТО. Схема (рис. 77) соответствующего эксперимента аналогична схеме 75 проведения опыта Саньяка с использованием полого вращающего диска с неподвижной коробкой в нем. Места крепления источника света и приемника перено­сятся с обода диска А на неподвижную основу коробки В, заключенную внутри диска А в условиях вакуума. Ес­ли при движении от неподвижного источника 1 к непод­вижному приемнику 2 и при движении от неподвижного источника 3к неподвижному приемнику 4частота фо­тонов останется неизменной как при вращении диска А, так и при его покое, то справедлива гравитационная тео­рия А. Эйнштейна.

Если же при неподвижных источниках и приемниках света и вращающемся диске А частота фотонов в направ­лении 1-2будет иметь фио­летовое смеще-ние, а в на­правлении 3-4красное сме­щение, то это будет свиде­тельствовать в пользу грави­тационной теории Г. Лоренца,

подтверждать существование Рис. 77 механического эфира и образова-ние в по­лости вращающегося ротора локального гравитационно­го поля.

Отмечу, что проблема с теоретическим объяснением данных экспериментов так и не была решена, если не считать [130-132]. Во всяком случае, я такого объясне­ния не встречал, а что касается самих экспериментов, то их, похоже, больше никто не повторял, и постепенно за­бывается о том, что они проводились. Итак, все описанные эксперименты (рис. 74-77) фик­сируют одно и тоже явление — локализацию (экраниро­вание) гравитационного поля в объеме полого вращаю­щегося диска. Причем важнейшим условием экрани­рования является полное отграничение динамическим объемом приборов, фиксирующих локализацию поля. Напомню, что гравипритяжение со времен Ньютона считается центральным, проходящим по прямой, соеди­няющей центры взаимодействующих тел, и многие экс­перименты проводились таким образом, чтобы «пре­рвать» зону данного взаимодействия как статическими, так и динамическими экранами (дисками, вращающими­ся либо в промежутке между телами, либо над притяги­ваемым телом, либо под ним). Но ни один из таких экс­периментов не был успешным. А это, в свою очередь, свидетельствует о том, что гравитационное притяже­ние передается внецентренно и может экранироваться только объемными динамическими стенками. Естест­венно также, что все эксперименты с локализацией гравиполя вращающимся пустотелым диском объясняются формулой (3.17).

Это очень показательный пример ортодоксального от­ношения к экспериментам, не вписывающимся в рамки современных теорий. И таких экспериментов не три, не четыре. Их десятки, а возможно, и сотни практически в каждом разделе физики, начиная с классической и кон­чая квантовой механикой. Даже в самом разработанном разделе физики — в классической электродинамике в достаточно узкой ее области электромагнетизме Г.В Николаев при­водит и пытается объяснить в работе [133] почти пол­сотни экспериментов, противоречащих теории. Понятно, что необъяснимость эта связана напрямую с отрицанием эфира и вместе с ним вещественной структуры эфирного пространства.

Дополнение И. Горячко

к закону притяжения

Обычно дополнение приводится автором в конце работы для разъяснения или обогащения текста некоторым новым материалом. Здесь я нарушаю традицию и привожу дополнение к главе, используя материал из книги И.Г. Горячко [45], который иным путем пришел почти к таким же выводам, по-своему формулируя законы механики. Считая его интерпрета­цию очень важной и оригинальной (хотя и не во всем совпадающей с излагаемым мной материалом), приво­жу отрывок из его книги.

«Рассмотрим задачу о движении планеты вокруг Солнца. Выбор планеты в качестве объекта иссле­дования обусловлен тем, что характер движения любой планеты оказывает самое непосредственное влияние на ход различных процессов, происходящих на планете и в ее атмосфере вследствие гравитационной состав­ляющей, присутствующей в любых этих процессах. Известно, что движение любой планеты происходит по замкнутой эллиптической орбите. В полярных координатах уравнение эллипса имеет вид [54,55]

r = P/l +e∙cosφ, (3.19)

где r – модуль радиуса-вектора траектории движения центра массы планеты; Р = L²_Tp/m²fM = а( 1 – е²) = const – параметр орбиты; L_Tp = rmw_Tp – модуль момента импульса планеты; т – масса планеты; М – масса Солнца; w_Tp – трансверсальная скорость планеты; е – эксцентриситет орбиты планеты; f = const – гравитационная постоянная; а = const – длина большой полуоси орбиты планеты; φ – полярный угол радиуса-вектора планеты.

Безразмерная пространственная координата планеты в ее плоском движении, как очевидно, равна:

r' = r/а = (1– е²)/(1 + e∙cosφ) = f₁(е,φ) (3.20)

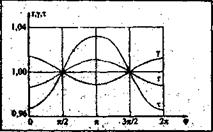
Вид функции r ' = f₁(e,φ) для одной из планет солнечной системы (Земли) представлен на рис. 23 (кривая r ')

Подставляя значение Р в равенство (3,19), находим:

w²_Тр = fМ (l +e∙cosφ)² /P = fM (l + e∙cosf) /r. (3.21)

Согласно работе [56], равенство (3.21) соответствует квадрату трансверсальной скорости планеты; квадрат же ее радиальной скорости равен:

w²_r = jMe²sin²φ/P = fMe²sin²φ/r (l + e∙cosφ), (3.22)

(Крайне важно иметь в виду, что трансверсальная и радиальная

Рис. 23.

составля­ющие полной скорости взаимно перпендикулярны, т.е. w_Тр ортогональна w_r).

Поскольку квадрат, полной скорости пла­неты в плоском дви­жении равен w² = w_Тр+w²_r, то с помощью равенств (3.21) и (3.22) находим [ 56]:

w²= fМ (1 + 2 e∙cosφ +e²) /P= fM (1 + 2 e∙cosφ +е²) /r (1 + e∙cosφ) = γfM/r. (3.23)

где γ = (1 + 2 e∙cos + е²) / (1 + e∙cosφ) = f₂ (e,φ) – некоторый безразмерностный переменный параметр (назо­вем его коэффициентом Горячко – А .Ч.) учитывающий волновой (т.е. периодический) характер распростра­нения гравитационной энергии в пространстве. Он жеопределяет и форму плоской траектории движения тела в пространстве. Равенство (3.23) можно получить и другим путем, если использовать известное из физики выражение для квадрата полной скорости планеты [57]:

w² = fM (2 /r – 1 /a),

заменяя в нем величину r с помощью уравнения (3.19) и подставляя величину а = Р /(1 – е²)

Нетрудно показать, что истинная траектория движе­ния планеты в пространстве, формирующаяся под воз­действием гравитации, представляет собой простран­ственную косинусоидальную кривую, форма которой определяется величиной параметра γ с некоторой (~2,8%) погрешностью. Поэтому для полного адекватного описания пространственного движения тела следует лишь уточнить вид этой математической зависимости. Для этого достаточно учесть, что одновременно с движением планеты вокруг Солнца перемещается и само Солнце. Поскольку, однако, точный вид этого параметра не имеет прин­ципиального значения для всех дальнейших выкладок, то на данном этапе исследования можно ограничиться рассмотрением плоского движения планеты. Вид функции γ = f₂ (e ,φ)для планеты Земля представлен на рис. 23 (кривая γ).

Проводя простейшие преобразования, из равенства (3,23) можно получить ряд новых и весьма важных количественных и качественных результатов. Так, умножая крайние члены этого равенства на массу планеты т, получаем ранее неизвестное соотношение [56]:

mw² = γfMm/r, (3.24)

или

2 Е = γП, (3.24')

где, в общем случае Е = mw²/ 2 + γω²/ 2- кинетическая энергия планеты; П = JMm/r – потенциальная энергия системы «планета-Солнце»: J – момент инерции планеты: ω – угловая скорость вращения планет, вокруг своей оси. Поскольку, однако, для планеты Jω² << mw², то с большой степенью точности можно принять Е = mw²/ 2.

Равенство (3.24) свидетельствует о взаимопревра­щаемости кинетической и потенциальной энергии при обращении планеты вокруг притягивающего центра (Солнца). В связи с этим выражение закона сохранения энергии для системы «планета-Солнце» (имея в виду знак минус для П), приобретает вид:

W = E – П = (γ – 2) П/ 2 = (γ – 2) Е/γ = const. (3.25)

Paвeнcтвa (3.24) и (3.25) свидетельствуют отом что распространение гравитационной энергии в пространстве представляет собой волно-

вой процесс. Для ус­ловий плоского движения планеты (полагая Солнце неподвижным) ее полная скорость равна:

w = ωr = 2 πr / τ,: (3.26)

где ω – круговая частота; τ – период обращения планеты вокруг Солнца. Поэтому из равенства (3 23) находим

γ = 4π²r³/τ²fМ (3.27)

Отсюда следует, что коэффициент Горячко равен g = f³ (r,τ). Это означает, что параметр g является про­странственно-временным параметром волнового процесса распространения гравитационной энергии. Он определяет пространственную удаленность планеты (в общем случае — тела), от ее притягивающего центра в любой момент времени. Подставляя в равенство (3.27) уравнение (3.19) и равенство Р= а (1 – е²), получаем:

а³/τ² = γfM (1 + e∙cosφ) / (1– е²) / 4 π² = γγ_tfМ/ 4 π², (3.28)

где g_t = [(1 + e∙cosφ) / (l – e²)]= f₄ (e,φ) – также безразмерный периодический параметр. Равенство (3.28) отличается от выражения третьего закона Кеплера лишь наличием множителей gg_t. Из этого равенства следует чрезвычайно важный качественный (гносеологический) результат:

r = 2 π√ (а³/γγ_tfМ) = f₅ (е,φ), (3.29)

или (в безразмерностном виде):

τ' = τ/τ_к = 1∕√ γγ_t = f₆ (е,φ), (3.29')

где х_к = 2π√ (a³/fM) = const – период обращения, определяемый третьим законом Кеплера.

Этот результат свидетельствует о том, что ход вре­мени, как физического параметра волнового процесса, всецело определяется текущими значениями параметров орбиты. Вид функции τ = f₆ (е,φ) для планеты Земля, представленный на рис. 23 (кривая τ), противоречит утверждению первого закона клас­сической механики о равномерно текущем времени:

В то же время кривые r, g, τ на рис. 23 свидетельствуют о том, что пространственно-временные параметры тел, находящихся на планете Земля, самосинхронизированы с параметрами орбиты планеты.

Совершенно аналогичный вид имеют кривые r, g, τ и для других планет Солнечной и любой другой орбитальной системы, отличаясь друг от друга лишь абсолютными величинами этих параметров, между которыми существует простое соотношение:

γ = r3∕τ2.

В этой зависимости заключена огромной важности информация о действительной роли пространства и времени в Природе, которую нам еще предстоит разгадать и понять.

Если теперь подставить выражение (3.29) в (3.27), то получим:

r = а³√γ_t = f₇(е,φ).

И вновь сталкиваемся с противоречием; изотроп­ности пространства, регламентируемого первым законом классической механики, не существует. Относя, как это принято в физике [53,57], величины М и r к условиям планеты, из (3.23) получаем:

w = √ (γfM/r). (3,30)

Формула (3.30) отличается от известных формул физики [53,57] того же назначения лишь наличием параметра g и поэтому является более общей. Так, при g = 1 с ее помощью можно определить первую космическую скорость; при g = 2 – вторую космическую скорость, при более высоких значениях параметра g – третью и другое космические скорости.

Если разделить обе части равенства (3.23) на r и отнести величины М и r к условиям планеты, то получим:

g = γg^о, (3.31)

где g° = – fM r /r²r – ускорение свободного падения тела (напряженность гравиполя в русской механике. – А. Ч.) в данной географической точке планеты. Например, для Земли: g^о = 9.78 м/с² – на экваторе; g° = 9.83 м/с² на полюсах. Умножая обе части (3.31) на массу тела, получаем весьма важный новый результат:

Р = γmg°, (3.32)

который свидетельствует о том, что вес тела на планете не является постоянной величиной, а также, как и ход времени, зависит от текущих значений параметров орбиты планеты. С ростом параметра γ вес тела в данной географической точке планеты увеличивается.

Разделив, наконец, обе части (3.24) на r и записав полученное выражение в векторном виде, находим (так как γω² << mw_r²):

mw_t² r /r∙r'/r = – γfMm r /r²∙r, (3.33)

F'_цс = – γF'_цб, (3.34)

где F'_цc – центростремительная сила; F_цб – центро­бежная сила.

Правая часть равенства (3.33) соответствует умно­женной на параметр γ силе F', определяемой формулой всемирного тяготения И. Ньютона (3.12), а левая – центростремительной силе. (Здесь учтено, что w_Tp ортогонально w_r, вследствие чего скалярное произведение w_Tp r /r = 0, и поэтому mw²_Tp/r∙ r' /r = 0.)

Соотношения (3.24), (3.25) и (3.34) имеют предельно общий вид. Это означает, что они применимы для любых орбитальных систем. В частности, с их помощью могут быть получены развернутые зависимости, описывающие движение электрона вокруг ядра атома (то есть электромагнитное взаимодействие), которое также является волновым процессом, полностью аналогичным процессу распространения гравитации.

Движение электрона по орбите принципиально не отличается от движения планеты. Поэтому плоская траектория движения электрона в пространстве и временные особенности его движения полностью определяются функцией g = f₂ (e,φ) = f_з (е,τ), где е – эксцентриситет электронной орбиты.

Отсюда следует вывод принципиальной важности: процессы распространения различных видов энергий в пространстве и во времени являются физически подобными.

Этим объясняется возможность и законность исполь­зования в классической механике метода обобщенных потенциалов и обобщенных координат.

Далее, если на графики функций r ' = f₁ (e,φ), g = f₂ (e,φ), τ' = f₃ (e,φ), построенные для какой-либо планеты Солнечной системы, нанести графики функций r_i = f₁ (e_i,φ), g_i = f₂ (e_i,φ), i, = f₃(е,φ), построенные для электронов, вращающихся на стационарных орбитах атомов химических веществ, составляющих таблицу Д. И. Менделеева (из которых состоит данная планета), то окажется, что эти графики совершенно однотипны. Это означает, что независимо от положения во времени и в пространстве, планета и электроны атомов постоянно пребывают в состоянии пространственно-временных соответ-ствий друг с другом. При этом часть электронов атомов (те из них, эксцентриситеты орбит которых близки по значению эксцентриситету орбиты самой планеты) находятся с этой планетой в состоянии пространственно-временного резонанса (т.е. являются энергети- чески скомпенсированными). Эти электроны ответственны за создание сил гравитационного происхождения на самой планете. Другая часть орбитальных электронов тех же самых атомов остается энергетически нескомпенсированной, образуя внутри и вокруг любого тела и самой планеты энергетические поля различной природы (тепловое, электромагнитное, химическое, гравитационное), то есть находящийся в беспрестанном движении эфир.

В связи с этим интересно отметить, что в геологии с некоторых пор существует классификация, разделяю­щая все химические элементы таблицы Д.И. Менделеева на четыре группы (отвечающие за степени дифференциации их по глубинам залегания в Земле): центро­бежные, центростремительные иокеанического происхождения. Указанная классифи­кация имеет важное практическое значение при определении месторождений тех или иных полезных ископаемых [58] и косвенным образом подтверждает справедливость изложенного.

Физическое подобие равносильно возможности описания процессов различной природы с помощью универсальных уравнений, представленных в обобщен­ных потенциалах и в обобщенных координатах, в которые лишь следует подставить соответствующие рассматриваемому типу взаимодействия значения физических величин. Поскольку во все полученные соотношения входит пространственно-временной параметр целесообразно остановиться на этом факте подробнее.

γ = 2 Е/П = (1+ 2 e∙cosφ + е²) / (1 + e∙cosφ) = f₂ (е,φ) = f₃ (r,τ) (А)

Из физики [53,57] известно, что отношение кине­тической и потенциальной энергии тела определяет форму его траектории в пространстве. При этом оказывается, что для замкнутых эллиптических траекторий полная энергия W < 0, для разомкнутых параболических W = 0и для гиперболических W > 0. Из геометрии [54] плоских конических сечений (эллипс, парабола, гипербола), кроме того, известно, что вид конического сечения всецело определяется величиной эксцентриситета е: для эллиптических сечений 0 < е < 1, (0 < g < 2); для параболических е = 1, (g = 2) и для гиперболических е > 1, (g > 2). Таким образом, форма траектории тела в пространстве может быть полностью определена либо знаком и величиной полной энергии W, либо величиной ее эксцентриситета е, либо величиной параметра γ по соотношению (А).

Для замкнутых эллиптических траекторий при нахождении тела (планеты, электрона в атоме) в перигелии орбиты (φ = 0 °)параметр g, согласно формуле (А), принимает максимальное значение: g_р = 1 + е, а в случае же нахождения тела в афелии орбиты (φ =180°) этот параметр принимает минимальное значение: g_а = 1 – е. Для Земли (е = 0,017), g_р = 1,017 и g_а = 0,983. Таким образом, погрешность, вносимая неучетом параметра g, в равенстве (3.34) составляет для Земли всего ±1,7% (см. рис. 23). Этим во многом объясняется тот факт, что второй и третий законы Ньютона, не содержащие этого параметра, оказываются достаточно точными для земных условий. Однако уже для таких планет, как Меркурий (е = 0,2066) и Плутон (е = 0,2530) эти законы оказываются ограниченно верными. И совсем неприменимыми они становятся для описания движения электронов на орбитах атомов (где реализуется диапазон 0< g <2), а также для тел, движущихся по параболическим (g = 2) и гипербо­лическим (g > 2) траекториям. Среднее же (для эллипти­ческих орбит) значение параметра g равно g_ср = (g_а + g_р) / 2= 1. Амплитуда кривой g = f₂ (e,φ)на рис. 23 равна, таким образом, g_а – g_р = 2 е.

Здесь следует обратить внимание на следующие принципиально важные обстоятельства.

Согласно соотношению (А), параметр g = f₂ (e,φ) = f₃ (r',τ')уже для электронных орбит атомов различных химических веществ приобретает смысл регулируемого параметра, способного при искусственном управлении им изменять как свою абсолютную величину, так и знак (вследствие периодичности функции cosφ). Очевидно, что это справедливо и для более глубоких уровней строения вещества, где происходят аналогичные беспрестанные движения соответствующих микротел вокруг притягивающих центров.

При е = 1, γ_мах= 2и g_тин = 0.Это означает, что при достижении величины эксцентриситета е = 1 происходит разрыв орбиты и она превращается в разомкнутую параболическую траекторию, характе­ризуемую величиной полной энергии W = 0. Последнее свидетельствует о величине минимально необходимой полной энергии, требуемой для того, чтобы материальное тело начало движение по параболической траектории, при котором реализуется наиболее экономичный режим его движения. Согласно соотно­шениям (3.24) и (3.25) при этом Е – П, т.е. происходит полная взаимопревращаемость кинетической и потенциальной энергии. Именно так движется фотон, который излучается или поглощается в период перехода электронов с одной на другую орбиту атома. При этом полная энергия фотона оказывается равной:

Дата добавления: 2014-11-29