Третье началоКТД известно как теорема Нернста [77,78], следствием которой является так называемый принцип недостижимости нуля абсолютной темпе­ратуры. 4 страница

Выше уже упоминалось, что обыкновенный отвес не занимает вертикального положения в тележке, движу­щейся с постоянной скоростью, но и не изменяет при движении угол своего наклона, а это и есть показатель абсолютности движения тележки с постоянной скоро­стью. Отклонение отвеса обеспечивается «уплотнением» эфира, а вместе с ним и напряженности внешнего гравиполя движущимся телом. И следствия «уплотнения» будут фиксироваться самыми различными приборами, включая простейший из них физический маятник. Рас­смотрим качественно взаимодействие с гравиполем ма­ятника, колеблющегося в тележке, движущейся с посто­янной скоростью.

Прежде всего, для тела, движущегося горизонтально с постоянной скоростью во внешнем гравитационном по­ле, последнее, как уже говорилось, не остается однород­ным для качающегося грузика-маятника, в то время как для самой тележки оно остается «уплотненно» однород­ным. Поэтому фиксировать движение любого тела с постоянной скоростью можно только такими прибо­рами, которые совершают собственное движение как относительно пространства, так и относительно те­лежки. Причем, например, угол отклонения отвеса в та­кой тележке определяет как характер «уплотнения» гравиполя, так и характер колебания маятника в этом гравиполе.

На рис. 35 качественно, без разбивки на такты, отра­жен один период колебания маятника в движущейся те­лежке, проходящей за единицу времени 1 см (маятник проходит от одной точки до другой, нумерацию точек см. на рис. 29).

Из рисунка 35 следует, что на протяжении одного пе­риода на каждом отрезке пути маятник имеет относи­тельно Земли, а, следовательно, и относительно гравиполя, различную скорость движения, которая складывается

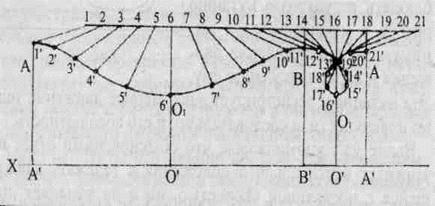
Рис. 35

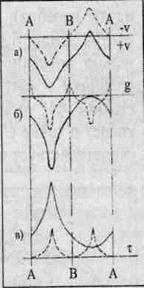
из скорости движения тележки и скорости колебатель­ного движения маятника. Проектируя скорости на ось XX получаем, что на участке АВ скорости тележки и ма­ятника складываются, а на участке ВА — вычитаются. Следовательно, в отличие от неподвижного относительно пространства маятника, у движущего полупериоды асимметричны. Асимметрия вызвана различными скоростями движения маятника относительно внешнего гравиполя, регистрируется по всем параметрам колебания и легко рассчитывается. На рис.36 графически изображено изменение парамет­ров направления и скорости v движения маятника, на­пряженности его гравиполя g, и периода колебаний τ в неподвижной тележке (штрихами) и в движущейся (сплошными линиями). На графике фиксируется четкая симметрия изменения параметров v, g, τ у маятника, колеблющегося в неподвижной тележке. Совершенно иная картина наблюдается при коле­бании в тележке, движущейся с по­стоянной скоростью. Все рассматри­ваемые параметры v, g, τ резко асимметричны. Отмечу, что асим­метрия не наблюдается при колеба­нии маятника в плоскости, перпен­дикулярной движению тележки. Асимметрия полупериодов коле­бания в плоскости движения позво­ляет эмпирически, находясь в закры­той тележке, определить состояние ее покоя или движения. Более того,
анализ других особенностей колебания позволяет в принципе найти скорость движения тележки, направление ее движения, массу и радиус тела или пространства, по которому

она движется. А это означает, что движение с постоянной скоростью абсолютно, а не относительно.

Вернемся к эксперименту, который Галилей проводил «в зале под палубой

какого-нибудь большого корабля».

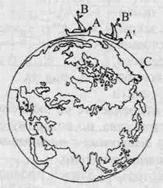
Естественно, что технические возможности средневековья не могли обеспечить тех скоростей и той высоты помещения, которые потребовались бы для фиксации, например, отклонения от вертикали падающей из круж­ки капли воды. Чтобы это отклонение зафикси-ровать, необходимо «кружку» подве-сить на мачте, на высоте 200-250 м, воду заменить мелкой дробью, равно- Рис. 36. мерную скорость корабля держать где-то 25-30 м/с. Что и сейчас на пределе технических возможностей. И если при дви­жении такого корабля с верхушки мачты уронить дро­бинку, то в своем падении она отклонится вперед по хо­ду больше чем на 0,5 мм. Последнее будет зафиксиро­вано приборами и подтвердит, что движение с постоянной скоростью абсолютно, а не относительно.

Абсолютность равномерного движения по поверхно­сти обусловлена тем, что фигура Земли не плоская, а круглая. И точки протяженного предмета (например, мачты корабля), находящиеся на разном расстоянии от центра Земли, будут иметь различную скорость относи­тельно поверхности. Поэтому если за время падения дробинки с мачты (рис. 37) ее основание пройдет рас­стояние АА, то верхушка — расстояния ВВ', и дробинка упадет в точке С, пройдя расстояние АС = ВВ'. А это и свидетельствует о движении корабля.

Рис. 37

Галилей, по-видимому, исходил из того, что изме­нения, происходящие в дви­жущемся теле, можно фик­сировать ощущениями. И, не уловив заметных отклоне­ний в поведении тел внутри корабля, он сделал вывод, что равномерное движение по криволинейной поверх­ности является относитель­ным. Именно поэтому прин­цип относительности распростра-нялся им только на круговые движения.

Это была формальная ошибка. Ее многократно усугу­бил Ньютон, распрямив круг и постулировав гипотезу об относительности прямолинейного равномерного движения. Именно прямолинейное движение названо позже А. Эйнштейном принципом относительности Галилея, хотя в действи­тельности он сам является его автором.

В результате в механике оказалось не просто две ошибки в понимании движения как процесса взаимо­действия, но и утвердилось как естественное понятие прямолинейности, никогда и нигде не подтвержденное экспериментально. Гипотеза прямолинейного и равно­мерного движения без взаимодействия постепенно стала единственной сущностью инерции. С одной сто­роны, она как бы объясняла само явление инерции, а с другой — превратилась из гипотезы в реальный факт относительности, не требующий подтверждения своей истинности.

Можно предложить проведение других эксперимен­тов, способных регистрировать иными приборами дви­жение с постоянной скоростью, например атомными ча­сами, гироскопами, световыми лучами и т.д., и все они будут подтверждать качественное отличие тела непод­вижного от движущегося.

Используемый классической механикой, как и теорией относительности, принцип относительности движения с постоянной скоростью полностью не вписывается в за­коны диалектики. Не вписывается потому, что состоя­ние покоя, т.е. то состояние, в котором центр масс од­ной системы не изменяет своего положения относительно центра масс другой, отличается от со­стояния движения в пространстве в первую очередь изменением качества. Представление о том, что про­странственное движение есть изменение качества и снова изменение качества, отсутствует как у Ньюто­на, так и у Эйнштейна. Вот это не наличествующее в механике свойство изменения качественного состояния при перемещении из одного места пространства в дру­гое необходимо использовать для эмпирического определения состояния движения. Причем все свойства тела в движении меняются, но меняются в различной про­порции и по-разному в направлении движения и ортого­нально ему. И эти изменения совершенно одинаковы как для «медленных», так и для «околосветовых» скоро­стей. Только эффективность качественного изменения свойств при этом, естественно, будет проявляться с раз­ной степенью наблюдаемости, да и наблюдения будут проводиться другой категорией приборов [41].

Именно уверенность Ньютона и позднее Эйнштейна в невозможности качественных изменений тел при отно­сительном движении, поддержанная научным сообщест­вом, стала психологической преградой на пути любых эмпирических проверок относительности движения. Они не рассматривались и не ставились не потому, что бы­ли невозможны для физического исполнения, а потому, что были невозможны постулативно. Физические по­стулаты превратились в ученый догмат, более жесткий и более действенный, чем догматы общественные и цер­ковные. Научный общественно-психологический запрет более жестко давит на личность, чем любые кандалы и запоры. Он сковывает мысль. Он запрещает вольный полет фантазии. Он навешивает шоры на разум и тормо­зит развитие и науки и общества.

Однако развитие науки со скрипом продолжается. По­являются эксперименты, не влезающие в обусловленные запретом ворота и потому отвергаемые ортодоксами с порога. (Вдумайтесь — факты в физике отвергаются только потому, что они противоречат запретительным постулатам.) Однако количество таких экспериментов накапливается. Их уже неудобно «заметать под поло­вик», велика становится куча, и делается как-то уже слишком непристойно использование в качестве основ­ного аргумента популярной шуточки «этого не может быть». Появляется необходимость, превращающаяся в потребность — объяснить, какова природа этих ненуж­ных и даже неприличных экспериментов, без наруше­ния запретов, без разрушения сложившейся ошибочной системы мышления. И чтобы миновать запрет незави­симо от того, понимают ли это исследователи или нет, разрабатывается мощный математический аппарат (как, например, в квантовой механике), сшивающий некорректные постулаты и подменяющий реальное понимание физических взаимодействий системой очень точных математических операций, подгоняющих решение под необъяснимые эксперименты. Конвенционализм математики обусловливает возможность такого развития фи­нки.

В качестве примера сшивания рассогласованных теорий можно привести также работу И. Пригожина «От существующего к возникающему». В ней для объясне­ния необратимости физических процессов, на основе сложного математического аппарата (потребовались супероператоры, стохастическая формализация с введени­ем вторичного времени и функционального не геометрического пространства) проводится достаточно формальное внесистемное самосогласование между динамикой и термодинамикой. И делается это с постулированием второго начала в качестве основополагающего динамического принципа, определяющего направление стрелы времени. Однако в этом аппарате отсутству­ет качественное изменение при взаимодействиях и ме­ханизм необратимости. Представление о механизме физических процессов подменяется математической символикой. Понимание сути физических явлений тоже ухудшается. И, следуя Бриллюэну [63], теория (напри­мер, теория относительности или квантовая механика) превращается в математическую фантастику, не имею­щую предсказательной ценности, а, следовательно, и пользы. Поскольку у теории нет способов предсказания введения тел в процессе физических взаимодействий, то не возникают и идеи экспериментов, подтверждаю­щих или опровергающих теорию. И все обсуждаемые к проведению эксперименты обкатываются в рамках заве­домо некорректных постулатов, образующих понятий­ный базис классической механики и всей физики.

3.6. Движение, ускорение, инерция

Наиболее сложными и наименее понятными пробле­мами механики Ньютона являются проблемы, связанные с движением, ускорением и инерцией. И хотя большин­ство ученых не сомневается в полной разработанности этих проблем и однозначного физического толкования их сущности (ведь существует четкий и отработанный математический механизм, описывающий количествен­но все нюансы движения тел в пространстве), эта уве­ренность — еще не основание для объяснения движения без взаимодействия, его сущности, возможности прямо­линейного движения с постоянной скоростью по инер­ции (относительное движение) и движения с ускорени­ем. Эта уверенность постулируется и может оказаться не описанием реального природного процесса, а только ос­новой для подгонки математического аппарата под оп­ределенные эмпирические данные. Гносеологические корни относительного и абсолютного движения остают­ся скрытыми и неясными для понимания, а, следователь­но, и для формализации процесса движения. Это следст­вие того, что в механике Ньютона нет онтологического ответа на вопросы: что есть движение и откуда оно бе­рется? Возможно ли существование прямолинейного движения по инерции как движения без взаимодейст­вия? Чем и как вызывается инерция? Возможно ли дви­жение тел в отсутствии гравитационного поля? Вопро­сов возникает очень много, и они требуют детального описания сущности механизма движения.

Как было показано выше, самодвижение тел — пуль­сация, является основой всех видов движения, вклю­чая перемещение относительно пространства, взаи­модействия с последним и вращение. Рассмотрим движение тела, например, стального шара радиусом – 25 см, плотностью ρ = 7,9 г/см³ по поверхно­сти без трения и с учетом его взаимодействия с вращающимся гравиполем Земли. Объем шара V = 6,54·10⁴ см3, масса т = 5,2·10² г, а вес Р = 5,168·10⁵ см.г.с^-2. Когда шар лежит на поверхности относительно неподвиж­но (т.е. его центр масс не перемещается по поверхности, а собственные колебания симметричны, не обеспечива­ют его перемещение и не принимаются во внимание), то все его параметры сбалансированы с параметрами Зем­ли. Ее везде принимаем невращающейся сферой с ра­диусом R = 6371 км и не имеющей атмосферы.

Шар, лежащий на поверхности, сам по себе не свобо­ден от нагрузок. Его объем сжат силой F, равной силе веса Р, но никакими приборами и измерениями это дав­ление не определить, поскольку ему подвергаются все элементы измерительных приборов. Именно это давле­ние есть следствие воздействия внешнего гравиполя на тело, и точно с таким же усилием тело сопротивляется внешнему давлению. Причем сопротивление грависжатию определяется свойствами тела, его структурой и строением и проявляется в некотором подобии форме силы Гука.

Важно понимать, что для внешнего наблюдателя вес тела есть его давление на поверхность Земли, а для самого тела вес — внешняя сила, обусловливающая ве­личину его деформации. То есть изменение параметров тела под воздействием гравиполя Земли является причиной возникновения веса.

Начнем разгонять тело по поверхности с постоянным ускорением и доведем скорость v движения до орби­тальной v' = 7,91·l0⁵ см/с. В процессе разгона вес тела Р, как это следует из классической механики, « уменьшается», а масса возрастает, что вовсе не следует из той же механики, и, при достижении первой космической скорости, становится равным 0. Естественно, что в процессе разгона меняются все свойст­ва тела, но механика Ньютона фиксирует только изме­нение силы притяжения и совершенно не объясняет физический механизм, вызывающий это изменение. Попробуем разобраться в этом вопросе.

По механике: при разгоне тела возникает ускорение а', направленное вер­тикально вверх и равное

а' = – v²/R.

Оно создает телу дополнительную подъемную силу F':

F' = – та'.

При достижении ускорением а величины ускорения свободного падения а = g подъемная сила F' становится равной весу шара Р. Происходит их взаимное погаше­ние:

P – F' = 0.

И в шаре, движущемся с первой орбитальной скоро­стью, возникает кажущееся состояние невесомости. Этот сценарий как бы подтверждается каждодневно демонстрацией невесомости космонавтами на космических кораблях. И потому указанное объяснение не вызывает никакого сомнения в своей справедливости. Но что произойдет, если усомниться в этом объяснении? И что может вызывать сомнение?

Сомнение вызывает исчезновение той силы — веса, которая является атрибутом тела. Т.е. не может исчезнуть по определению. Если же она исчезла, то и тело, в структуру которого входит эта сила, тоже исчезло, и все предыдущее объяснение являются математическими манипуляциями и становится некорректными.

Как уже говорилось, вес тела обусловлен силой, с которой оно сжимается напряженностью g гравиполя Земли. Когда тело начинает двигаться, возникающее ускорение а (дополнительная напряженность, вызываемая уплотнением гравиполя Земли) не отнимается, а прибавляется к напряженности внешнего гравиполя. И сила сжатия возрастает:

F' = mа'.

И потому движущееся с ускорением тело воспри­нимает возникшую силу F' как дополнительное сжи­мающее воздействие, вызывающее пропорциональное возрастание деформации. К силе веса Р = F, действующей на него в статическом состоянии, при движении стала добавляться сила F' которая при орбитальной скоро­сти сравнивается с силой F = F' и на тело действуют две силы:

F + F' = 2 F = 2 Р.

Это дополнительное воздействие напряженности гравиполя на движущееся тело, обусловленное взаимодействием тела с эфирным пространством, вызывает изменение всех его свойств. Подчеркну, что собственный инвариант свойств шара для сжимающей силы F и в статическом и в динамическом состоянии не меняется. Внешняя си­ла F' изменяет количественную величину свойств, но не внутренние взаимосвязи. Используя это качество, нахо­дим по КФР для шара инвариант, связывающий радиус r с силой F в статике:

F²r⁵= 2,608·l0¹⁸ – const. (3.70)

Поскольку инвариант (3.70) остается неизменным как для статики, так и для динамики, то с изменением силы F до 2 F величина const не изменится, но вместе с силой изменяются количественно все свойства тела, включая его радиус r. Определим, как изменится величина радиуса r' при движении шара с орбитальной скоростью подставив в F²r⁵ = 2,608х10¹⁸ величину 2 F = 1,0336·10⁶, и решив относительно r' получаем:

r' = 1,895·10 см.

Таким образом, приобретение телом орбитальной скорости сопровождается деформацией его радиуса почти на четверть размера в статическом состоянии. Это важнейший результат для понимания диа­лектики движения тела во внешнем гравитационном поле. Именно им определяются все физические процес­сы, сопровождающие движение. Именно он является подтверждением качественного и количественного из­менения состояния тела при переходе от статики к динамике. И именно отсюда следует физическое пред­ставление о механизме движения с ускорением и дви­жении по инерции.

Рассмотрим, как изменяются количественно другие свойства движущегося тела, например масса т и напря­женность гравиполя g. Связь массы с радиу­сом определяется инвариантом:

т²r = 6,938·10⁶ – const'. (3.71)

Подставляя в (3.71) r = 1,895·10 см, определяем массу m' тела, движущегося с орбитальной скоростью:

m' = 6,05·10² гр.

По силе и массе определяем напряженность g' грави­поля:

g' = 2 F / m' = 1,708·10³ см/с². (3.72)

Результат (3.72) можно получить непосредственно из инвариантной взаимосвязи радиуса шара r и напряжен­ности внешнего гравиполя g:

r²g' = 6,13110⁵ – const'. (3.73)

Подставляя в (3.73) величину радиуса этого уплотне­ния r', имеем:

g' = 1,708·10³ см/с².

Напряженность g' внешнего гравиполя в окрестностях тела изменилась и выросла в 1,71 раза. А это значит, что изменилась пульсация тела, вызывая при движении уп­лотнение своей эфирной шубы. В результате этого уп­лотнения возросла напряженность внешнего гравиполя в окрестностях шара. Именно уплотняющая шуба, кото­рая возникает при любой форме движения, за счет взаимодействия с внешней средой сохраняет изменив­шуюся пульсацию тела относительно постоянной и не позволяет телу сбросить свою деформацию.

Таким образом, расчеты подтверждают диалектиче­ский вывод о том, что движущееся тело качественно отличается от неподвижного, и ни о какой тождест­венности между ними не может быть речи. Любое пере­мещение тела в гравитационном поле есть качествен­ное изменение его состояния, сопровождаемое дефор­мацией, изменением напряженности собственного гравитационного поля и других свойств. С другой сто­роны, взаимодействуя с эфиром, движение тела вызыва­ет деформацию, возрастание и уплотнение шубы, изме­нение внешней напряженности гравитационного поля вокруг тела.

Вывод о том, что физические тела в движении с любой скоростью деформируются при взаимодействии с эфи­ром, может быть подтвержден эмпирически. В печати несколько лет назад появилась информация, что одно из государств строит электромагнитное орудие, способное сообщать снаряду на выходе из ствола скорость до 8·10 км/с при собственной массе снаряда до 100 г (или весом под 100 кг).

Это орудие может быть использовано для проведения эксперимента. Для этого надо сообщить ядру диамет­ром, например, 12-16 см скорость, близкую к орбиталь­ной, и на его пути установить световой экран с фотоэле­ментами или плотную, но проницаемую мишень. Причем мишень должна отстоять от «дула» на некото­ром расстоянии. Если ядро в полете изменяет свой ради­ус, а расчеты показывают, что ядро радиусом 16 см и массой около 80 г при скорости порядка 8 км/с умень­шится в диаметре примерно на 3 см, то экраны зафикси­руют это изменение. По-видимому, уменьшение объема ядра происходит не симметрично, а в направлении дви­жения в большей степени, а в перпендикулярном в меньшей, т.е. ядро принимает форму чечевицы. Поэтому следы в мишенях могут оказаться иными по величине, чем это следует из расчета. Величина уменьшения зави­сит также от свойств материала, из которого изготовле­но ядро.

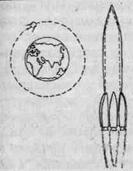
Можно предложить другой, не менее сложный экспе­римент с использованием вращающегося на орбите кос­мического аппарата. При пролете этого аппарата над оп­ределенной зоной к его орбите запускается ракета с приборами с таким расчетом, чтобы высота подъема ра­кеты оказалась равной высоте орбиты. Сама ракета должна находиться в нескольких сотнях метров в сторо­не от орбиты и точно в тот момент, когда аппарат будет пролетать мимо нее (рис.38).

Рис. 38.

Рас­стояние от ракеты до аппарата должно быть с максимальной точ­ностью зафиксировано как прибо­рами ракеты, так и с Земли. И в самый момент пролета космиче­ского аппарата, когда ракета зави­сает напротив него и почти непод­вижна относительно пространства, ее инструменты фотографируют аппарат по определенной про­грамме. После обработки материа­лов на снимках можно убедиться, что размеры космического аппара­та почти на четверть меньше тех размеров, которые он имел на поверхности Земли (на рис. 38 обозначены штрихами).

По современным представлениям, неравномерное движение тела в пространстве может быть только уско­рением. Само ускорение понимается как скорость изме­нения скорости. Поэтому при движении тела с постоян­ной скоростью его ускорение как бы равняется 0. Однако имеются два особых случая, когда это правило нарушается и ускорение оказывается не связанным с не­равномерным движением тела.

Первый случай — свободное падение отпущенного над поверхностью Земли тела под действием силы притяже­ния. Оно происходит с постоянным ускорением, в точ­ности равным напряженности гравитационного поля Земли, и равенство это объяснения не имеет. Молчаливо допускается, что тождественность ускорения и напря­женности есть случайное совпадение.

Второй случай — появление центростремительного или нормального ускорения при движении тела по окружно­сти с постоянной по модулю скоростью. Возникающее при этом тоже постоянное ускорение а' описывается со­мнительной для думающих физиков формулой:

а' = v²/R,

где v – угловая скорость, R – радиус окружности.

Появление ускорения а' в данном случае оказывается физически непонятным и даже подозрительным, по­скольку оно не исчезает и остается неизменным, пока тело движется по окружности с постоянной скоростью. Подозрительно же оно потому, что по своей размерно­сти и поведению при вращении весьма напоминает на­пряженность гравиполя Земли, тем более что и сила, вы­зываемая ускорением а тела массой т, кажется аналогичной силе притяжения. Физическое объяснение этого явления тоже отсутствует. Подозрительное отно­шение к центростремительному ускорению привело к путанице в понимании физической сути вращения, к за­мене понимания механизма движения хорошо отлажен­ным аппаратом математического формализма.

Поскольку тело при любом движении с ускорением в гравитационном поле деформируется, то эта деформа­ция вызывает изменение количественной величины всех свойств тела, включая на­пряженность его собственного гравитационного поля. Деформация прекращается и сохраняется, когда тело переходит от ускоренного движения к равномерному. Так же сохраняется достигнутая напряженность соб­ственного гравиполя тела. Наблюдаемое нами ускорен­ное движение тела для самого тела является просто изменением величины напряженности собственного гравитаци­онного поля. Переход на движение с постоянной скоро­стью — сохранение достигнутой напряженности своего гравиполя. Замедление движения — раздеформация те­ла, уменьшение напряженности собственного гравипо­ля. Таким образом, понятие «ускорение» и «изменение напряженности гравиполя» есть одно и то же поня­тие. Оно характеризует один и тот же процесс — грави­тационную деформацию тел. Только этот процесс фиксируется внешним наблюдателем как ускорение, а для тела является изменением напряженности собственного гравиполя. Тела, на поверхности Земли, постоянно под­вержены деформации напряженностью внешнего грави­поля. Эта деформация вызывает изменение напряженно­сти гравиполя тел, которое остается в дальнейшем постоянной и обозначается нами как неизменное уско­рение свободного падения. Подъем тела над поверхно­стью Земли приводит к изменению напряженности внешнего гравиполя или, что то же самое, ускорения свободного падения, которое сопровождается строго пропорциональным изменением напряженности грави­поля поднимаемого тела.

Поскольку ускорение есть наблюдаемое извне след­ствие изменения напряженности собственного гра­виполя движущегося тела, то естественно, что при движении с постоянной скоростью, при которой на­пряженность собственного гравиполя остается неиз­менной в течение всего движения, внешний наблюда­тель фиксирует отсутствие ускорения при равно­мерном движении. И делает вывод, что скорость может существовать отдельно от ускорения.

Таким образом, изменение напряженности грави­тационного поля движущегося тела и ускорение его движения есть один и тот же процесс, имеющий два названия. Только первое характеризует статическое со­стояние напряженности тела, а второе — изменение этой напряженности при движении с ускорением. Поэтому возникновение любого ускорения в любом движении есть проявление изменения напряженности гравипо­ля движущегося тела, вызываемое внешними грави­тационными силами.

Изменение напряженности гравиполя движущегося тела связано с еще одним физическим явлением, назван­ным Ньютоном инерцией. Инерция, по его опреде­лению, «...есть способность сопротивления, по кото­рой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает свое состоя­ние покоя или равномерного прямолинейного движения» [2]. Рассмотрим сущность инерции.

Итак, тело, движущееся в пространстве с ускорением, взаимодействует с гравитационным полем, деформирует и изменяет под его воздействием напряженность собст­венного поля и плотность своей шубы. Изменение де­формации, плотности шубы и напряженности самого те­ла не может происходить без приложения определенной силы, без затрат энергии на компенсацию этих процес­сов и, следовательно, без сопротивления силе, движу­щей тело в пространстве с ускорением. Вот это сопро­тивление тела попыткам изменения своего состояния, т.е. попыткам деформировать его, и есть то, что Ньютон называет врожденным свойством тела — инер­цией.

Повторимся. В случае, когда тело внешней силой вы­водится из состояния покоя и разгоняется, деформация тела, возрастание и уплотнение шубы, взаимодействие с эфиром тормозят его движение и фиксируются нами как стремление сохранить состояние своего покоя, т.е. тело проявляет свойство инертности. От­сюда инертность — степень деформации тела, дос­тигнутая в процессе изменения напряженности соб­ственного гравиполя под воздействием извне. Рассмотренный в данном разделе пример с переходом тела радиусом r = 25 см от неподвижного состояния на поверхности к движению по инерции с первой космической скоростью показал, что в результате перехода ра­диус деформируется до величины r' = 18,4 см. Именно деформация, обусловленная воздействием эфира, вызывает сопротивление изменению движения и становится инертностью тела. Сама же деформация, а вместе с ней и асимметрия собственной пульсации тела обеспечивает последующее движение по орбите за счет постепенной раздеформации. Можно по­казать, что аналогичный эффект вызывается опусканием тела в гравитационном поле.

Дата добавления: 2014-11-29