Третье началоКТД известно как теорема Нернста [77,78], следствием которой является так называемый принцип недостижимости нуля абсолютной темпе­ратуры. 6 страница

ε = g /R = g²/v² = vg/R²ω = v²g²/FG = v²gM/FR² =... и т.д.

А это достаточно основательная демонстрация физи­ческой значимости углового ускорения. Для выявления ее физической сути приравниваем правые части уравне­ний (3.87) и (3.88) и, произведя преобразования, получа­ем:

ε = v²/r²= ω². (3.91)

Угловое ускорение, таким образом, по модулю есть квадрат угловой скорости. Подставляя вместо ее вели­чину из (3.91) в (3.85), находим полное ускорение рото­ра, вращающегося с постоянной скоростью:

а_i = r_i√ (ω⁴ +ω⁴) = r_iω²√ 2 = v_iω√2. (3.92)

Уравнение (3.92) показывает, что при вращении рото­ра с постоянной скоростью наличествует угловое уско­рение, имеющее определенный физический смысл, а главное — нормальное и тангенциальное ускорения рав­ны между собой и тангенциальное ускорение не равно 0. Поэтому сложившееся представление о физической сути вращения ротора с постоянной скоростью оказывается некорректным.

Как уже было показано, вращение любого тела в эфи­ре сопровождается его взаимодействием с эфиром и гра­витационным полем. Следует различать взаимодействия с эфиром тела, движущегося за пределами оси враще­ния, и тела, движущегося вокруг неподвижной оси, находящейся внутри объема тела. Если в первом случае тело взаимодействует с эфиром асимметрично, вызывая различные по объему напряжения, то во втором, когда ось находится в геометрическом центре ротора, проис­ходит симметричное взаимодействие пространства тела с пространством эфира. Следствием этих взаимодейст­вий является возникающая нормальная сила F_n с векто­ром, направленным по радиусу к оси (рис. 48) в точном соответствии с уравнениями (3.74)-(3.78):

F_n = та_п при а_п = g_p,

где g_p – напряженность гравиполя вращающегося рото­ра.

Сила F_n распределена по всему ободу и деформирует ротор (рис. 47, б ) сжимающими к центру частями силы ∆F_n. Когда ротор приходит во вращение, «обволаки­вающая» его эфирная шуба пре­вращается в эфирный диск, плотность и величина которого определяется как свойствами ротора, так и его скоростью вращения. Именно эфирный диск обусловливает

поведение гироскопов, «сгоняет» планеты в плоскость Солнца, а спутники в плоскость планет, и может быть зафиксирован грави-мет­рами, поведением микроорганиз-мов внутри диска, пре­ломлением лазерных лучей и другими спосо- Рис. 48. бами.

Одновременно в тангенциальном направлении будет действовать внешняя сила, вызываемая тангенциальным ускорением и равная произведению массы ротора на ус­корение:

F_t = ma_t при a_t = g_p.

Если ротор отключить от подачи внешней энергии, то под воздействием силы F_t он будет продолжать вра­щаться до тех пор, пока не произойдет полная раздеформация его объема. В этом случае накопленная деформацией энергия ротора расходуется на взаимодей­ствие с внешним эфиром, который наравне с воздухом, трением и другими причинами тормозит вращение ро­тора.

Возникновение, отсутствующей в современной меха­ник, внешней неуравновешенной силы F_t, вызываемой взаимодействием тела с внешним вещественным про­странством, как при движении на нерастяжимой ни­ти, так и при вращении твердого тела на оси, является принципиальным подтверждением существования в природе гравиоотталкивания, обусловливающего воз­можность создания движителей, исполь­зующих это свойство для движения искусственных ап­паратов за счет отталкивания от гравиполя Земли.

Эти внешние силы получили в современной механике название фиктивных, мнимых, несуществующих сил инерции, поскольку их носитель — эфир игнорировался. Можно предложить проведение различных экспери­ментов, подтверждающих существование сжимающей силы F_n и возникновение внешней силы F_t. Начну с экс­периментов, способных доказать изменение объема ро­тора под действием силы F_n при вращении (рис. 49).

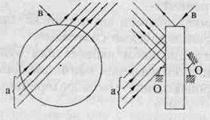
Ротор, боковая поверхность и обод которого отшли­фованы до зеркального блеска, устанавливается на оси ОО. На его боко­вую поверхность под малым углом направляются не­сколько парал- лельных лучей света а (напри­мер, лазерных), которые, отразившись, попадают на отдален­ный экран. Один из лучей b таким же образом падает на обод ротора и отражается на отдаленном экране. Контрольная настройка приборов производится при очень медленном вращении. При номинальном количестве оборотов в се­кунду в соответствии с теорией будет наблюдаться от­клонение на экране падающих лучей. Оно покажет, ка­кие изменения происходят с параметрами диска при переходе от состояния покоя к быстрому вращению.

Рис. 49

Можно провести и более простой эксперимент. Тот же, но уже не шлифованный, ротор укрепляется на оси ОО, и на его боковые поверхности и обод наклеиваются тензодатчики, фиксирующие поверхностную деформа­цию тел. Тензодатчики на боковинах соединяются по­следовательно и выводятся на приборы через мост Уитстона через контактные токосъемники, расположенные на оси. Если при вращении ротора его объем подверга­ется деформации, то тензодатчики зафиксируют эту де­формацию и однозначно определят ее характер. (Однако этот эксперимент достаточно ненадежен и может ока­заться безрезультатным, если совпадут по величине де­формации тензодатчика и ротора.)

На использовании внешней силы F_t работают маятник Ю.Г. Белостоцкого [68], устройства БМ-28, БМ-35 А.И. Вейника [69], турбинка А.А. Селина [70], двигатель Ж.Ж. Мари [71], «атомы» Р.И. Романова [72] и некото­рые другие (например, инерцоиды Толчина [73]). Од­нако авторы этих устройств, не зная о возникновении внешней силы F_t при движении тел и вращении ротора с постоянной скоростью, предполагают, что имеют дело с нарушением третьего закона Ньютона с про­цессом безопорного перемеще­ния в пространстве.

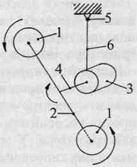
Опишу из них только устрой­ство маятника Ю.Г. Бело­стоцкого (рис. 50). Он включает два гироскопа 1, жестко закрепленных по концам штанги 2, способной вращаться с помощью электродвигателя 3вокруг оси 4, проходящей через середину штанги пер­пендикулярно ей. Все устройство подвешивается с по­мощью одностепенного шарнира 5 на жестком стержне 6к потолку.

Рис. 50

При раздельном раскручивании штанги с не вращающимися гироскопами или только гироскопов эффект не проявляется. Но если привести во вращение штангу и гироскопы, прибор начинает качаться пропорционально скорости вращения штанги с большой амплитудой коле­бания. Классическая механика допускает такие колеба­ния, но они оказываются неприемлемыми для ортодок­сов.

Можно предложить иную конструкцию устройства, работа которого сопровождается появлением внешней силы F_t.

Рис. 51

Возьмем два ро­тора-гироскопа 1 и электромотор 2, ось которого укреплена неподвижно и пер­пендикулярно гори­зонту. На оси электромотора 3закрепим шарнирно планку 4(рис. 51, вид сверху), по краям которой уста­новлены гироскопы 1 с осями, параллельными оси элек­тромотора. Вот и вся конструкция.

Раскрутим гироскопы против часовой стрелки до дос­тижения ими постоянной частоты и после этого начнем вращать электромотором планку с гироскопами тоже против часовой стрелки, фиксируя изменение нагрузки электромотора. У меня при проведении этого экспери­мента два гироскопа мощностью по 3 Вт так перегрузи­ли 400-ваттный электромотор, что он сгорел, так и не достигнув нормативного количества оборотов.

Повторяю, что в данных экспериментах проявляется внешняя сила, представление о которой отсутствует в современной механике. Эта сила остается неизвест­ной, поскольку угловое ускорение, трактуемое как гео­метрическое свойство и потому не являющееся свойст­вом физическим, своим математическим исчезновением в режиме равномерного вращения обусловливает такое же исчезновение силе F_t и тангенциальному ускорению a_t. Если быть последовательным и признавать систем­ную взаимосвязь между свойствами тел, в частности ро­тора, то вместе с, a_t и F_t должны исчезнуть все ос­тальные свойства тела, а, следовательно, и само тело. Поскольку последнее не происходит, необходимо опре­делить физическую сущность углового ускорения.

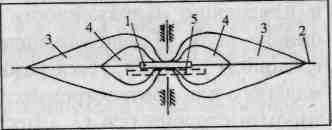
Рис. 52

Следует еще раз отметить, что эфирная шуба у вра­щающегося ротора превращается в эфирный диск, сжимающий ротор.

На рис. 52 схематич­но показана конфигу­рация эфирного диска, имеющего следующую структуру. Ротор 7, плоскость вращения ротора 2, зона дефор­мированной напряженности гравиполя (зона диска) 3, область наибольшей деформации 4. Диск представляет собой зону уплотненного эфира, а, следовательно, и воз­росшей напряженности внешнего гравиполя. Напряжен­ность области наибольшей деформации и обусловлива­ется свойствами ротора и скоростью вращения. Можно подобрать такие параметры ротора, вращения и внеш­них тел, что гравидиск будет притягивать к себе тело 5 в зоне 4 при вращении ротора в замкнутом кожухе. (Тело 5показано пунктиром.) О возможности возникновения эфирного диска упоминается в работе [70].

Есть информация, что такие эксперименты успешно проводились в конце 80-х годов В.М. Ереминым (г. Аст­рахань). У него к ротору, как к магниту, «прилипали» плиты, и не только металлические, весом свыше 10 кг, а вода «обволакивала» кожух.

Следует отметить, что именно деформация вращаю­щегося ротора и возникновение эфирного диска обеспе­чивают появление необъяснимых на сегодня свойств гироскопа [74] и без понимания свойств эфирного диска мы так и не приблизимся к пониманию механики движения гироскопа.

Рассмотрим сущность этого движения и силы, возни­кающие при быстром вращении твердого однородного ротора (рис. 47, б). В полном соответствии с уравнения­ми (3.74)-(3.78), которые описывают именно круговое движение точки на ободе ротора, взаимодействие ротора с эфиром приводит к сжатию ротора, к его деформации и изменению напряженности собственного гравитаци­онного поля. Изменение напряженности собственного гравиполя и фиксируется нами как возникновение нор­мального или центростремительного ускорения а_п с век­тором в сторону оси О. Вместе с деформацией ротора происходит асимметричное изменение его собственной пульсации в направлении вращения, которое закрепля­ется деформацией и вызывает возникновение тангенци­ального или касательного ускорения a_t. Эти ускорения — следствие деформации ротора — обусловливают как бы появление двух сил:

F_n = т'а_п, F_t = ma_t,

из которых центростремительная, или нормальная Fn, поддерживает деформацию ротора, а другая, тангенци­альная F_t внешняя, поддерживает его вращение. Именно она вращает ротор, когда к нему не подводится энергия, и он продолжает вращаться по инерции, т.е. сила F_t есть внешняя реальная сила инерции.

Ротор при вращении постоянно находится под слож­ным суммарным воздействием сил F_n и F_t и напряжен­ности гравиполя Земли, которая при вращении заставля­ет молекулы ротора вибрировать. Особенность всех этих воздействий в том, что они имеют полевой характер и действуют по объему на все молекулы ротора. И как бы ни был, по нашему мнению, плотен и однороден ротор, эта плотность не сохраняется на уровне молекул. По­этому при вращении по-разному изменяется частота собственного колебания молекул как относительно друг друга, так и по диаметру ротора. А это вызывает стрем­ление молекул к изменению своего положения, приво­дит к усилению местного дисбаланса плотности и к воз­никновению многочисленной локальной микровиб­рации. Дополнительное воздействие на микровибрацию будет оказывать сжатие ротора силой F_n, направленной от плоскости обода к оси. Поскольку сила действует равномерно по сходящейся к оси, то любая ее внешняя величина как бы стремится при схождении к бесконеч­ности. Под действием этой силы происходит сжатие ротора, вызывающее перемещение молекул (рис. 47, б). А так как плотность и особенно вибрация молекул по диамет­ру ротора неодинакова, то и сжатие их будет неравно­мерным и вызовет появление по нейтральным зонам мо­лекул многочисленных очень мелких трещин, а вместе с ними и возрастание частоты локальной вибрации объема ротора. Где-то на треть радиуса суммарное воздействие этих факторов будет постепенно достигать критической величины, и если оно сопровождается возрастанием уг­ловой скорости вращения, то последняя ускорит рост микротрещин в направлении возрастания напряженно­сти поля ротора, т.е. к ободу. Рост трещин сопровожда­ется возникновением и усилением биения ротора, а это достаточно быстро приводит к его развалу. Оторвав­шиеся куски, становясь самостоятельными системами, улетают по тому же закону, что и тела, вращающиеся на нити при ее обрыве.

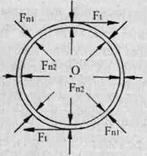
Несколько иную форму будет иметь деформация кольца, вращающегося вокруг своего геометрического центра. Поскольку тело кольца не является сплошным, то его центр вращения находится за пределами про­странства, образуемого кольцом. Эта особенность при­водит к тому, что его тело испытывает сразу оба опи­санных выше воздействия, центростремительное и центробежное. А на наружный и внутренний обода кольца действуют, вызываемые взаимодействием с гравиполем эфира, два нормальных ускорения а_п1 и а_n2 (рис. 53), направленные в противоположные стороны и создающие силу, сжимающую тело кольца по радиусу как изнутри F_n2, так и снаружи F_n1 окружности. Возни­кает также и тангенциальная сила F_t, вращающая коль­цо. Поэтому из всех вращающихся вокруг геометриче­ского центра фигур, кольцо способно выдержать наибольшие скорости вращения.

Рис. 53

Естественно, что критерием каждого вывода должна быть практика. Справедливость одно­го из данных способов может быть подтверждена эксперимен­тально:

• изменением объема ротора при вращении (эксперименты описаны в данной работе – рис. 48);

• изучением характера деформации кристаллической струк­туры ротора при вращении;

• анализом системы микротрещин оптическими и электромагнитными способами;

• почти полным отсутствием площадки текучести у оторвавшихся частей ротора.

3.8. К «абсолютности» скорости света

С начала ХХ столетия принцип постоянства коли­чественной величины скорости света в пустоте оставался одним из наиболее эмпирически под­твержденным постулатов общей теории относительности. (Предпола­галось, что пустота это не вакуум, а некое вместилище, в котором нет никаких тел, самостоятельная и независимая сущность.) Одновременно постулировалось, что количественная ве­личина скорости света является предельной скоростью движения материальных тел и распространения электро­магнитных волн и что скорость передачи гравитационных взаимодействий по количественной величине равна скоро­сти света. Никакого физического обоснования последнему постулату не приводилось, и до сих пор он остается при­нимаемым на веру. Наиболее распространенная формули­ровка абсолютности скорости света приведена в работе [75]: «…скорость света в вакууме не зависит от скорости источника, во всех инерциальных системах отсчета одинакова и равна 3·10¹⁰ см/с».

В этой коротенькой формулировке в неявной форме за­шифровано несколько физических явлений, не подтвер­ждаемых экспериментами и не соответствующих законам диалектики.

Известно, что скорость света во всех веществах различ­на, и утверждение об ее постоянстве в вакууме гносеоло­гически означает, что вакуум веществом не является, свойства вакуума (если они наличествуют) изотропны, скорость движения света не зависит от его свойств (точнее свет, как и пространство, не имеет свойств). Вакуум и свет — не взаимодействующие системы, и фотон не является веществом. Отсюда следует однозначный гносеологиче­ский вывод: и свет и вакуум не вещественны, не матери­альны, и вакуум есть не что иное, как пустота, не имеющая свойств. Поэтому постулирование абсолютности скорости света есть не только физическое, но и гносеологическое утверждение.

Поскольку скорость движение вещественных частиц —фотонов, которые (по современным представлениям) не имеют массы покоя, а следовательно, не материальны и существуют только в движении, то основным фиксируе­мым их свойством, их философской сущностью становит­ся движение. Но диалектика определяет сущность не как абсолютное понятие, а как относительное. И, переходя от абстрактной сущности к конкретному движению фотонов света, свойство относительности, понимаемое как отсутст­вие абсолютной скорости равномерного движения, сохра­няется, что не отражается на абсолютном характере самого движения (всякое движение тел в вещественном про­странстве абсолютно). Поэтому можно утверждать, ба­зируясь только на положениях диалектики, что скорость света всегда относительна, и искать, какие причины при­вели к постулированию постоянства скорости света и ка­кие эксперименты могут доказать его относительность. Начнем с первого.

Основными факторами, определяющими движение све­та, являются:

• среда (везде принимается телесное пространство), в которой движется свет;

• скорость течения времени в данной среде;

• расстояние данной среды, проходимое светом за еди­ницу времени;

• свойства движущихся фотонов.

При движении света, например в воздухе, определяем количественную величину всех этих факторов. Когда луч света переходит из воздуха в другое вещество, он покида­ет одну среду (одну систему) и переходит в другую среду (в другую систему). В процессе движения он взаимодей­ствует сначала с одной средой, а потом с другой, имею­щей иные качественные величины свойств. Поэтому для новой среды следует определить количественную величи­ну скорости света, плотность и скорость течения време­ни. Вследствие изменения среды показатели всех факто­ров должны измениться. Как экспериментально зафик­сировать эти изменения — вопрос технический. Прин­ципиально то, что новое вещество должно иметь иную количественную величину всех факторов, которые опре­деляют величину скорости света.

Однако в современной физике эти факторы рассматри­ваются по величинам, получаемым для воздушной среды, а если и признается, что скорость света и плотность раз­личны для различных сред (что естественно), то скорость течения времени считается одинаковой для всех сред, включая пустоту. Такой вывод автоматически постулиру­ет постоянство скорости течения времени для всех сред (для всех веществ). Система взаимосвязи свойств наруша­ется, и картина физического явления скорости света ста­новится неадекватной природе.

Вводя принцип постоянства скорости света, Пуанкаре и следовавший за ним Эйнштейн (вне зависимости от сво­его желания) неявно ввели в физику постоянство течения времени и одинаковую плотность всех вещественных про­странств во всех областях Вселенной. И потому все по­следующие экспериментальные проверки постоянства скорости света проводились таким образом, что ско­рость света заранее принималась неизменной, а экспери­мент строился так, чтобы подтвердить сложившийся вывод (по принципу среда и свет — не взаимодействующие системы).

Известно, что скорость света, проходящего через грани­цу двух сред, меняется пропорционально углу преломле­ния света при переходе из одной среды в другую. Исполь­зуя это свойство и то, что с повышением давления воздуха скорость света в нем не остается неизменной, можно про­вести следующий эксперимент.

В камеру, приспособленную для работы с газом при по­вышенном давлении и имеющую устройство для измере­ния угла преломления света при варьировании давлением, помещаются выверенные хронометры различных типов. Изменяя давление воздуха в ней, замеряют отклонение светового луча. Снаружи, рядом с камерой, помещают контрольный хронометр, выверенный с теми, что находят­ся в камере. При сжатии воздуха в камере скорость хода часов в ней будет меняться пропорционально углу пре­ломления светового луча, проходящего через камеру. Ос­новываясь на взаимосвязи течения времени t, и скорости светового луча с (это параметры одной системы), можно записать:

ct = c't', (3,94)

где с, с' – скорость света в эфире и в сжатом воздухе, t, t' скорость течения времени и с ≠ с' и t ≠ t'. Из (3.94) находим t':

t' = ct/c'. (3.95)

Соотношение с/с' = п – коэффициент преломления све­тового луча при переходе из одной среды в другую:

t' = nt. (3.96)

Таким образом, скорость течения времени в камере с плотностью ρ будет отличаться от течения времени в ка­мере ρ ' в п раз, где п – коэффициент преломления света при переходе луча из среды ρ в среду ρ'.

Расчеты, проведенные по формуле (3.96) для определе­ния изменения скорости течения времени в камере при по­вышении давления и изменения плотности воздуха, при­водятся в табл. 9. В ней использованы значения плотности сжатого воздуха в атмосферах и коэффициент преломле­ния из [76].

Таблица 9

№ п/п	Р	п	t
	1,00	1,0002929	-
	18,84	1,0043480	6 мин. 15 с.
	42.13	1,0124100	17 мин. 52 с.
	69,24	1,204400	29 мин. 26 с.
	96,15	1,0284200	40 мин. 55 с.
	123,02	1,0363300	52 мин. 19 с.
	149,53	1,0442100	63 мин. 39 с.
	179,26	1,0521300	75 мин. 00 с.

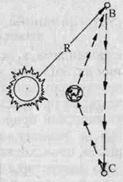
Можно провести и более сложный эксперимент, осно­вывающийся на том, что пространство вокруг небесных тел анизотропно, и скорость прохождения электромагнит­ных волн в данных пространствах будет значительно от­личаться от абсолютной. Последнее можно показать сле­дующим экспериментом. Предположим, что на орбиту вокруг Солнца, на расстоянии R > 800 млн. км выведены два спутника В и С так, что расстояние между ними l = ВС > 1,5R (рис. 54). Можно показать, что скорость радиосигнала, проходящего между Землей и спутниками, будет за­висеть от того, какой путь он проделает. Рассмотрим два пути движения сигнала. В первом случае сигнал, послан­ный из А в В, отразившись от В, возвращается в А, где от­разившись идет в С, и из С возвращается в А. Во втором случае сигнал идет из А в В, отразившись от В, в С, откуда возвращается в А (на рис. 54 указано стрелками).

Если рассматривать геометрическую длину пути, то путь АВ-ВА-ВС-СА будет более чем в два раза длиннее пути АВ-ВС-СА. Следовательно, при постоянстве скорости света время, затраченное на прохождение сигналом первого Рис. 54. пу­ти, будет больше, чем на прохождение второго, и мы бу­дем иметь однозначное подтверждение постулата об абсо­лютности скорости света в эфире.

Если же физические размеры про­странства остаются неизменными с изменением геометрических разме­ров, то время, затраченное радио­сигналом на прохождение расстояния АВ-ВА-АС-СА, будет почти вдвое меньше, чем время, потраченное на путь АВ-ВС-СА, и на всем участке не будет ни одной области, где скорость света сохранится постоянной.

В отличие от величины скорости света, которая на эквипотенциальной поверхности Земли определяется достаточно хорошо как теоретически, так и экспериментальными метода­ми, в отношении определения скорости распространения гравитационных волн никакого прогресса не наблюдается. Эта скорость не только неизвестна (постулируется, что она равна скорости света) но и, похоже, не имеется ни одного предложения по ее экспериментальному определению. Надо полагать, что отсутствие информации о скорости гравитационных взаимодействий отрицательно сказывает­ся на понимание природы гравитации. К этому вопросу мы еще вернемся.

4. Основы термодинамики И. Горячко

Обобщая основы русской механики, охватывающей все разделы физики, я не предполагал включать в нее раздел «Термодинамика», поскольку самому мне нико­гда не приходилось иметь дело с данной наукой. В пе­риод пребывания в Санкт-Петербурге инженер-капитан первого ранга И.Г. Горячко подарил мне свою книгу [44] поразившую меня простотой логики, насыщенно­стью материала и оригинальностью подхода к объясне­нию термодинамических явлений. Объяснения, совпа­дающего во многих аспектах с положениями русской механики. Практически эту работу можно было посчи­тать готовой главой, и я счел возможным включить, с разрешения И.Г. Горячко, его материал в книгу.

4.1. Принципы, методы и основные соотношения

классической термодинамики

Возникнув в середине XIX века первоначально как теория тепловых машин, к настоящему времени класси­ческая термодинамика (КТД) переросла в науку, изу­чающую процессы самой разнообразной физической и химической природы, связанные с превращением энер­гии и изменениями физико-химических свойств ве­ществ, происходящих при таких превращениях.

Из литературы [77, 78] известно, например, что клас­сическая термодинамика успешно применяется для опи­сания тепловых процессов, фазовых переходов и пре­вращений. Известны примеры применения ее для объ­яснения принципа действия гальванического элемента, магнитотермического эффекта, поведения диэлектрика в электрическом поле, излучения абсолютно черного тела, определения вольтамперных характеристик электрод­ных ламп, протекания химических процессов и т.п.

Математический аппарат классической термодина­мики основан на законе сохранения энергии термодина­мической системы (ТДС) и принципе существования эн­тропии, на основе чего получено основное уравнение классической термодинамики — ее первое начало.

Первое начало КТД является выражением полного дифференциала удельной внутренней энергии и имеет вид [77, 78]:

du = Tds – pdv = δg – δl, (4.1)

и, s, v, q, l – удельные: внутренняя энергия, энтропия, объем, внешняя теплота, внешняя работа деформации термодинамической системы.

Физический смысл равенства (4.1) заключается в том, что изменение внутренней энергии термодинамической системы связано с изменением внешней теплоты и со­вершением внешней работы деформации термодина­мической системой.

Если рассмотреть обычно приводимый в литературе [77,78] вывод соотношения (4.1), то нельзя не видеть, что такой вывод совершенно не учитывает того, что од­новременно с протеканием процесса внешнего подвода теплоты к термодинамической системе (внешнего энер­гообмена) внутри вещества термодинамической систе­мы протекают процессы, связанные с совершением ра­боты трения микрочастиц и выделением или погло­щением теплоты трения (внутреннего энергообмена). Поэтому можно ожидать, что равенство (4.1) может оказаться не полным.

Дата добавления: 2014-11-29