Третье началоКТД известно как теорема Нернста [77,78], следствием которой является так называемый принцип недостижимости нуля абсолютной темпе­ратуры. 2 страница

Рис. 28

Угол поворота зависит от упругости нити подвеса и ма­териалов, из которых изготов-лено кольцо.

Таким образом, для объясне­ния экспериментов, фиксирую­щих отличную от законов Нью­тона, напряженность гравиполя тел при перемещении по высоте или различное ускорение при «свободном» падении, нет не­обходимости привлекать гипо­тезу о «пятой силе». Эти разли­чия обусловливаются неодина­ковым сжатием перемещаемых по высоте тел или соответст­вующим торможением их в па­дении гравиполем Земли.

Отмечу еще раз, что всякое перемещение тела по высоте сопровождается измене­нием напряженности внешнего гравиполя, деформацией тела, а также изменением его энергетического со­стояния. Возникающая деформация увеличивает кине­тическую энергию тела при опускании (тело, деформи­руясь, уменьшается, кинетическая энергия накаплива­ется, потенциальная убывает). При подъеме же тела происходит его раздеформация, процесс накопления энергии меняется на противоположный. Именно взаим­ное превращение кинетической и потенциальной энер­гии при подъеме и опускании тела, связанное с дефор­мацией, обусловливает механизм возвратно-поступа­тельного движения маятника (рис. 29).

Маятник, тело-груз, подвешенное на невесомой нити в гравиполе Земли с неподвижной точкой закрепления О, при максимальном отклонении в точке А и симметрич­ной ей точке В имеет наименьшую деформацию, а сле­довательно, и максимальную потенциальную энергию.

Рассмотрим структуру колебания маятника с непод­вижной точкой подвеса О. На рис. 29 схематично пока­зано движение маятника за один период. Оно складывается из двух одинаковых полупериодов АД и ВА. На схеме путь АВ разбит на 10 участков. Точки 1...11 перво­го полупериода показывают место нахождения маятника в каждую последующую единицу

Рис. 29

времени при движении от точки А в точку В. И соответст­венно, точки 11.... 21при движении от В к А. Из рис. 29 видно, что АВ и ВА полно­стью симметрич-ны. Так же симметричны АО₁ и O₁B. Маятник, выходя из точки А, за полный период про­ходит через все точки дважды (кроме точки 11). В каж­дой точке (кроме 1 и1l)маятник два раза имеет одина­ковую по модулю скорость движения. Таким образом, структура движения маятника в обоих полупериодах одинакова. Она сохраняется при колебании в любой плоскости. Время колебания во всех последующих пе­риодах равно первому.

Это внешняя картина наблюдаемого движения. Если же рассматривать колебания маятника как процесс взаимодействия грузика с гравитационным полем Земли, то каждый полупериод необходимо разделить на два такта, соответствующих стадиям деформации и раздеформации тела грузика в движении.

I такт. Когда в точке А грузик отпускается, то под действием внешнего гравиполя и нити в падении он на­чинает двигаться к точке О₁. Движение определяется де­формацией тела-грузика и накоплением кинетической энергии, которая в точке О₁, достигает максимума. Здесь первый такт — деформация — заканчивается и начинается второй — раздеформация.

II т а к т. Перейдя точку О₁ грузик, используя нако­пившуюся, кинетическую энергию, продолжает движе­ние с раздеформацией до тех пор, пока в точке В вся кинетическая энергия не перейдет в потенциальную. Вто­рой такт — раздеформация — закончился, и процесс повторяется в обратном порядке.

Все параметры колебания маятника сохраняются симметричными до тех пор, пока напряженность внешнего гравиполя остается горизонтально однородной, верти­кально уменьшающейся с высотой. Само колебание ма­ятника по своему характеру аналогично колебанию, вы­зываемому механическим растяжением пружины.

Равномерное или ускоренное перемещение подвеса с маятником в любом направлении нарушает однород­ность воздействия внешнего гравиполя на маятник, обусловливает асимметрию его колебания. Характер асимметрии определяет-ся процессом перемещения, вы­зывающим деформацию или раздеформацию как тела, маятника, так и окружающего гравитационного поля. А это означает, что состояния маятника с непод­ вижным или движущимся подвесам качественно раз­личаются между собой, и это различия будет фикси­роваться приборами, находящимися, например, внутри закрытой тележки. Ниже я использую асимметрию ко­лебания для доказательства абсолютности всякого движения. Здесь же приведу описание и объяснения од­ного очень интересного эксперимента с маятником, про­веденного И.М. Крюковым.

Почти четверть века назад И.М. Крюков сформули­ровал простенькую задачу о движении маятника, кото­рая до настоящего времени ставит в тупик специалистов механиков, как теоретиков, так и экспериментаторов, своей кажущейся неразрешимостью. И это притом, что процесс колебания маятника представляется наиболее изученным механическим процессом, а элементы ответа на вопрос излагаются во всех учебниках физики.

Задача может быть сформулирована в следующей форме:

Как значительно (на десятки процентов) изменить эмпирический период колебания маятника, не изменяя длину его подвески и напряженности внешнего грави­тационного поля?

Если, согласно механике, принять что период колеба­ния маятника определяется только этими двумя пара­метрами, то никаких способов его значительного изме­нения просто не может быть. И именно к такому выводу чаще всего приходят специалисты, рассматривая эту за­дачу. Однако такой вывод нельзя признать удовлетвори­тельным, поскольку кроме вышеуказанных физических параметров существует и возможность изменения вза­имного положения подвески и грузика маятника. Дру­гими словами, грузик может быть неподвижным относи­тельно подвески (иметь одну степень свободы) или свободно двигаться относительно ее, превращаясь в не­которое подобие ротора (иметь две степени свободы). И именно эта возможность оказывается фактором значи­тельного варьирования периода колебания маятника. Рассмотрим, что происходит с периодом при колебании с одной и двумя степенями свободы. Имеем грузик 1на подшипнике 2установленном на оси 3(см. рис. 30). Подшипник 2обеспечивает возможность свободного поворота грузика относительно подвески 4, а сама под­веска 4 вращается в подшипниках 5. Устройство 6 – за­мок, который может заклинивать грузик, обусловливая ему в движении одну или две степени свободы. Пока­жем, в полном соответствии с ньютоновской механикой, что частота колебания при одной степени свободы будет значительно отличаться от частоты колебания того же маятника с двумя степенями свободы. Рассмотрим коле­бания маятника с одной степенью свободы. (Грузик за­клинен, массой подвески пренебрегаем.) 1. Введем следующие обозначения: J – момент инерции грузика 1 относительно оси 3; m – масса грузика: l – длина подвески (расстояние от центра оси 3 до центра оси 5-5); Q – угол отклонения маятника; g – напряжённость внешнего грави- Рис. 30. тационного поля (ус­корение свободного падения); Т₃ – кинетическая энергия маятника с одной степенью свободы; Т_n – кинетическая энергия маятника с двумя степенями свободы.

Отметим, что при ко­лебании с одной степе­нью свободы грузик маятника участвует как в падении (изменение положения по высоте), так и в повороте вместе с подвеской 2 относи­тельно гравиполя Земли и его кинетическая энергия определя-ется уравнением:

Т₃ = JQ²/ 2 + тl²Q/ 2. (3.42)
Тогда функция Лагранжа будет равна:

L = (J + ml²) Ò /2 + mglсosO. (3,43)

Для O (t) имеем уравнение:

(J + ml²) Ö = – mglsinO. (3/44)

Если угол O мал, то уравнение (3.43) может быть записано иначе:

Ö + g/l·O/ (1 + J/ml²) = 0. (3.45)

И частота малых колебаний ω₃ равняется:

ω₃ = √(g/l (1 +J/ml²)] = (1 + J/mll²) ^1/2√ g / l (3.46)

Это хорошо известное уравнение движения физиче­ского маятника.

2. При двух степенях свободы незакрепленный грузик в своем падении независим от вращения подвески (не поворачивается относительно гравиполя), следствием чего становится другая величина его кинетической энер­гии, потому будет иметь место иная частота колебания. Обозначим угловую скорость поворота грузика на оси 3 через к. Тогда кинетическая энергия Т_к равна:

Тк = ml²Ò²/ 2 + J/ 2 к², (3.47)

а функция Лагранжа;

L = ml²Ò²/ 2+ J/ 2 k² + mglcosO. (3.48)

И для угла О получаем уравнение:

ml²Ö = mglsinO. (3.49)

Откуда находим частоту малых колебаний ω:

ω_к = √g//l. (3.50)

А это (3.50) не менее известное уравнение движения математического маятника.

Однако в современной механике никакой физической связи между уравнениями (3.46) и (3.50), кроме подобия в форме записи, не просматривается и потому предпола­гается, что они описывают как бы различные виды дви­жения. Что касается поворота грузика вокруг оси 3, то для угла поворота ω имеем уравнение:

d(Jк)/dt = 0.

Откуда, при угловой скорости поворота грузика рав­ной углу поворота подвески, получаем: к = const.

Превращение маятника из физического в математиче­ский только за счет изменения степени свободы грузика, сопровождаемой изменением кинетической энергии ко­лебания, при неизменной потенциальной энергии воз­можно только в том случае, если период колебания ма­ятника определяется силовым взаимодействием с каким-то внешним полем и величина взаимодействия зависит от формы закрепления маятника.

Из формул (3.46) и (3.50) явствует, что единственным внешним силовым полем, которое может влиять на пе­риод колебания маятника, является гравитационное по­ле. В формулы входит напряженность гравитационного поля и, следовательно, только она определяет период колебания маятника при неизменной длине подвески, но с изменением способа его закрепления.

По логике рассуждения, принятой в ньютоновской ме­ханике, мы не можем перейти от (3.46) к (3.50), что и обусловливает как бы независимое существование в фи­зике математического и физического маятников. Но та­кой переход должен наличествовать. Ибо это не две независимые формулы, отображающие различные движе­ния маятника, а формализация одного процесса проте­кающего в различных условиях, определяемых формой его закрепления, а, следовательно, и взаимодействие ма­ятника с гравитационным полем окружающего про­странства. Формулы (3.46) и (3.50) отличаются на величину к, равную:

к = (1 +J/ml²)^-1/2.

И создается впечатление, что эта величина к = const является постоянным параметром, поскольку включает в себя неизменные величины m, l, r. Поэтому предполага­ется, что между физическим и математическим (?) дви­жением маятника существует некий необъяснимый ска­чок, например типа квантового.

Однако более вероятно, что механизм взаимодействия маятника с гравиполем обусловливает возможность по­стоянного изменения к в зависимости от движения под­вески и грузика относительно осей 3 и 5. Исходя из это­го можно провести преобразования, изменяющие формализацию коэффициента к, и получить следующую зависимость:

к = (1 + r²/ l²)^1/2. (3.51)

И в числителе и в знаменателе дроби правой части (3.51) стоят радиусы грузика r и подвески l. Так как ско­рость вращения обода грузика равна произведению его радиуса на частоту, то в общем случае будем иметь для него скорость v₁:

v₁ = rω.

Откуда:

r = v₁ / ω. (3.52)

И для подвески:

l = v/ω₁. (3.53)

Поскольку в формулах (3.52) и (3.53) частота ω имеет, в случае физического маятника, одинаковую количест­венную величину, то, подставляя (3.52) и (3.53) в (3.50), находим зависимость коэффициента к от скорости пово­рота обода ротора относительно поворота подвески:

к = (1+ v₁²/v²)^-1/2. (3.54)

И окончательно формула (3.46) имеет вид:
ω = √ g/l ·(1 + v₁²/v²)^-1/2. (3.55)

Формула (3.55) показывает, что период колебания ма­ятника обусловливается отношением квадрата скорости его поворота v₁ к квадрату скорости поворота подвески v, а потому при жестком закреплении грузика, когда его скорость относительно подвески v₁ = 0, мы имеем дело с математическим маятником, который с началом свобод­ного поворота грузика превращается в физический. А это позволяет посредством изменения жесткости за­крепления грузика варьировать период колебания маятника, как в сторону возрастания, так и в сторону за­медления, что кажется невозможным по механике Ньютона.

Эксперименты с изменяемой степенью свободы маят­ника (а это и названо маятником Крюкова), проведенные в 1988 г. в ЦАГИ В.П. Якуниным и Н.Г. Панферовым, показали, что изменение степени свободы с одной на две меняет частоту колебания маятника на величину, пре­вышающую 30%.

Теоретически можно показать; что максимальный период достигается только тогда, когда коэффициент становится равным к = √2 = 1,414...

Формула (3.55) свидетельствует о безразличном по­ложении подвески относительно горизонта, а потому эксперимент с изменением степеней свободы ротора-грузика может иметь множество разновидностей, как бы не имеющих никакого отношения к маятнику.

Один из вариантов вертикального закрепления рото­ров по обе стороны оси 5 описан в данной работе. Вто­рой, не имеющий на первый взгляд никакого отношения к маятникам, предложен самим И. М. Крюковым и на­зван мною «Рамка Крюкова» [48]. Суть эксперимента заключается в следующем (рис. 31):

Внутри металлической рамки l, установленной на оси АВ в подшипниках, расположены планки 7 и 8 с грузи­ками 2, способными свободно перемещаться по план­кам. Грузики с одной стороны прикреплены к боковинам рамки пружинами, а с другой имеют петли 3и, пе­редвигаясь, растягивают пружины до крючков 4,кото­рые и удерживают пружины в растянутом положении. Крючки 4 тягами 6 соединены со спусковой кнопкой 9. Если в таком положении (грузики имеют одну степень свободы) рамку раскрутить вокруг оси АВ (сообщить ей определенный момент количества движения) и оста­вить ее вращающейся, то до останова пройдет две-три минуты.

Рис. 31

Если же после раскручивания, нажать кнопку 9 то освобо­жденные грузики 2 под действием пру­жин устремятся к оси АВ (грузики получают две степени свободы). Пока они сходятся к оси, рамка раскручивается в соответствии с «законом» сохранения количества движе­ния. Но достаточно грузикам перейти ось АВ, как вра­щение рамки мгновенно тормозится почти до полной ее остановки. Грузики раздеформируются. Момент их им­пульса нейтрализуется, количество движения уменьша­ется и сохраняется только момент импульса рамки. «За­кон» сохранения количества движения как бы нарушается, поскольку система останавливается за счет «внутренних» сил.

Все вышеописанное позволяет сделать следующие выводы:

• маятник является гравитационным прибором и характер его движения определяется способом дефор­мации с гравитационным полем Земли:

• «физический и математический» маятники разли­чаются эмпирически только количеством степеней свободы, а, следовательно, и способом взаимодействия с гравиполем.

3.4. Инерциальные и гравитационные

силы и массы

Провозглашение классической механикой эквивалент­ности инерциальной и гравитационной масс при распро­странении на взаимодействия логически приводит к за­ключению, что эффект, вызываемый ускорением, экспериментально невозможно отличить от аналогично­го эффекта, вызываемого гравитационным притяжени­ем. Этот эффект, используемый Д. Эйнштейном в построении теории гравитации, предполагает возможность рассмотрения в течение малого промежутка времени и в пределах небольшой области пространства гравитационного поля как приблизительно постоянного и однородного. Вот как иллюстрируется принцип эквивалентности в ра­боте [61]:

«Предстают себе космическую ракету, пролетающую так далеко от гравитирующих тел — звезд или планет, что гравитационные силы, действующие на ракету, ни­чтожно малы. Пусть мощность ракетных двигателей по­добрана так, чтобы ускорение, с которым движется ра­кета, в точности равнялось ускорению свободного падения g. На космонавта, который сидит в ракете, действует единственная сила — реакция опоры со стороны кресла N. Именно эта сила сообщает космонавту уско­рение: согласно второму закону Ньютона N = mg, где т – инертная масса космонавта. Космонавт помнит, что перед стартом, когда ракета стояла неподвижно на Зем­ле, на него со стороны кресла действовала сила N, урав­новешивающая силу притяжения к Земле, т.е. N' = m'g. И в том, и в другом случае у космонавта создавалось ощущение, что какая-то сила вдавливает его в кресло. Если т = т', то N = N'. Значит, если гравитационная и инертная массы совпадают, то и в том и другом случае кос­монавт должен испытывать совершенно одинаковые ощущения: т.е. он, закрыв наглухо иллюминаторы, не смог бы угадать — неподвижна ли ракета, но вблизи есть тело, создающее гравитационное поле с напряженностью g, или гравитационное поле отсутствует, но ракета движется с ускорением g».

И далее следует сильный вы­вод: «никакой локальный эксперимент, т.е. экспери­мент, проводимый в малой части пространства, в изо­лированной лаборатории, не позволяет отличить гравитационное поле от ускорения».

Уверенную аргументацию авторов, физиков-экспери­ментаторов по профессии, достаточно легко опроверг­нуть, предложив им провести простой эксперимент с маятником, помещенным вместо ракеты в обыкновен­ный лифт, движущийся с постоянным ускорением.

В своем движении лифт, изменяя положение точки за­крепления маятника по высоте, а вместе с ней и напря­женность внешнего гравиполя. воздействует на дефор­мацию и раздеформацию тела-маятника, и, следова­тельно, на процесс перехода потенциальной энергии в кинетическую и наоборот. Отсутствие данного перехода приводит к быстрому затуханию колебания маятника. Поэтому в своем колебании тело маятника будет прохо­дить один первый такт. Второй — раздеформация — зави­сит от количественной величины ускорения и при уско­рении, превышающем проекцию амплитуды на верти­кальную составляющую, наблюдаться не будет, что и зафиксирует наличие в кабине лифта инерциального по­ля. Таким простейшим способом не только космонавт, но и лифтер может достаточно быстро убедиться в том, что имеет дело не с мощным внешним гравитационным полем, а с движущейся ускоренно «изолированной» ла­бораторией.

Убеждение, что сила инерции и сила тяготения есть разные, но сводимые друг к другу силы, лежит в основе всех гравитационных теорий и сопровождается предло­жением иных мыслимых экспериментов, как бы под­тверждающих принцип эквивалентности и способных создать условия, при которых силу тяготения невозмож­но отличить от силы инерции. Так в работе [62] предла­гается следующий опыт по его подтверждению:

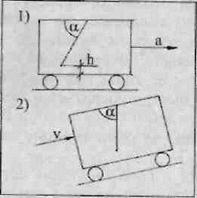
«Пред­ставим себе совершенно закрытый вагон, который движется по горизонтальному полотну дороги с посто­янным ускорением (рис.32, 1). В таком вагоне отвес бу­дет отклоняться от направления, которое мы на Земле называем вертикальным. Равнодействующая силы инер­ции и силы тяжести отклонит отвес к задней стенке ва­гона. В вагоне все будет так, как если бы вагон подни­мался с постоянной скоростью в гору (рис. 32, 2). А величина силы тяжести равнялась бы сумме действи­тельной сил тяжести и силы инерции в ускоренном, но горизонтально движущемся вагоне (понятно, что надо брать геометрическую сумму векторов). Так как в обоих случаях все тела получают совершенно одинаковые ус­корения, нельзя узнать, что происходит с вагоном на са­мом деле: движется он равномерно в гору при увеличе­нии силы тяжести или ускоренно по ровному месту, если пользоваться только приборами, регистрирующими вес, и не знать подлинной величины силы притяжения к Земле. Если за окнами будет темно, то никакого способа различить силы, нет. Сила притяжения к Земле и сила инерции проявят себя как физически тождественные».

Рис. 32

Данная задача сформулиро­вана более хитро, чем экспе­римент с ракетой, хотя заключение столь же категорично — нет способов различения инер­ции и гравитации. Автор зада­чи — теоретик помнит, что при движении с ускорением а вес тела меняется, и при длительном наблюдении в ускоренном вагоне это изменение буде зафиксировано. Вот почему нельзя пользоваться весами. По этой же причине второй вагон не стоит наклонно, а движется в гору с постоянной скоростью. В нем тоже будет наблюдаться эффект уменьшения веса.

Поскольку в классической механике свойства не зави­сят друг друга, то иных способов обнаружения состояния движения больше не предлагается, хотя таких спо­собов множество. Простейший из них позволяет обна­ружить движение вагона с ускорением с помощью обыкновенного метра. Для этого достаточно, оказав­шись в вагоне, замерить расстояние h от пола до грузика отвеса. Подождав некоторое время, повторить замер, и если обнаружится изменение h, то, значит, вагон дви­жется с ускорением. Если h осталось неизменным, вагон с равномерной скоростью поднимается в гору.

Более сложные эксперименты, например, с помощью зеркала и зайчика от направленного на него и отражен­ного на отдаленный экран луча света или с помощью интерферометра Майкельсона, позволяют, находясь в закрытом вагоне, визуально наблюдать его перемещение с ускорением в сантиметрах и даже в долях миллиметра, т.е. с меньшим, чем развивает улитка.

Чем же обусловлены столь серьезные заблуждения в понимании сути физических процессов, связанных с движением тел?

Эти заблуждения определяются постулативным ха­рактером начал механики, отсутствием системной взаимосвязи между ними, полным совпадением резуль­татов теоретических расчетов элементов движения с экспериментальными данными и некоторой предсказа­тельной способностью механики. В частности, при опи­сании движения наличествуют следующие явные и не­явные постулаты:

• рассматриваются отдельные свойства тел и их изме­нение при движении, а не взаимосвязанное изменение всех свойств;

• произвольно разделяются массы на инертную и гра­витацион-ную, что искусственно раздваивает силы на инерциальные и гравитационные;

• предполагается тождественность тел в покое и дви­жении;

• движение тела отрывается от эфирного пространства и гравитационного поля;

• постулируется неизменность и независимость про­странства от тел, которые в нем движутся;

• предполагается возможность существования скоро­сти без ускорения, отсутствие зависимости, как между ними, так и с движущемся телом;

• постулируется относительность прямолинейного и равномерного движения;

• вводятся искусственные инерциальные системы отсчета;

• и самое главное — отсутствует представление о том, что тело, неподвижное относительно пространства, качественно отличается от того же движущегося любым способом тела. И это отличие всегда можно зафиксировать приборами, находящимися внутри него.

Проиллюстрирую как, базируясь на вышеперечислен­ных постулатах, возникает неадекватное природе пред­ставление о сущности движения.

Сначала отмечу, что не все из перечисленных посту­латов исторически принадлежат Ньютону. В частности, у него отсутствует понятие «инерциальные системы от­счета» как абстрактное «геометрическое и кинематиче­ское определение, заключающее в себе нереалистиче­скую идеализацию» [63] и описание событий в терминах этого понятия. В своей механике Ньютон использовал представление о коперниковой системе, отображающей реальное физическое пространство — вместилище, за­полненное эфиром. Такое представление до некоторой степени напоминает понятие о месте Аристотеля. И именно поступательное движение тела относительно пространства, эфира и тел, находящихся в них без взаи­модействия с первыми, становится у него движением по инерции. Неинерциальным оставалось движение с уско­рением, и только потому, что оно обусловливалось либо воздействием внешних сил, либо вращением.

Введение последователями Ньютона представления об инерциальных системах отсчета стало деформацией ньютоновской механики, превращало эти системы в са­мостоятельные сущности, делало излишним представление о физическом пространстве и совсем ненужным понятие «эфир». Первым это заметил и сразу же отбросил эфир, как и эфирное пространство — Эйнштейн, сна­чала заменив пространство как реальность пустотой и координатными мнимостями, а затем инерциальными системами отсчета. И поэтому в современной физике вещественное пространство описывается не как те­лесное образование, взаимодействующее со всеми те­лами, а как абстрактное пустое вместилище, заполнен­ное не взаимодействующими с пространством полями и телами.

В теории функции инертного пустого пространства приписаны мыслимым инерциальным системам отсчета. Прямым следствием введения инерциальных систем оказался произвольный отрыв движения тела от вещественного про­странства и превращение последнего в инерциальную, первичную систему отсчета (в которой можно помес­тить неподвижного наблюдателя), а тела - во вторич­ную систему отсчета (в нее усаживается движущийся наблюдатель). Наблюдателей, как дополнение к инерци­альным системам отсчета, впервые использовал Мах.Естественно, что наблюдатель понимает наблюдаемое событие не таким, каким оно происходит в природе, а таким, каким оно должно быть по той теории, при­верженцем которой является ученый, посадивший этого наблюдателя (не случайно А.А Денисов наименовал их «зеваками» [64]). Являясь исполнителями субъективных устремлений ученого, они как бы выполняют функцию «независимого прибора», подтверждающего предлагаемые посылки, и потому наблюдатель в тележке не должен замечать взаимодействия движущегося тела с веществен-ным про­странством, что до него и за него делает автор теории, превращая субъективные домыслы в «реальную» дейст­вительность и демонстрируя кажущуюся относитель­ность этого движения.

Приведу еще один пример описания поступательного движения с ускорением тележки (вторичной системы) относительно инерциальной коперниковой первичной системы отсчета. По горизонталь­ным рельсам с пре­небрежительно ма­лым трением катит­ся тележка (вторич­ная система отсче­та), увлекаемая за­крепленном на блоке грузом (рис. 33). На тележке мас­сой т установлен отвес массой т'. Опускаемое под дей­ствием притяжения Земли тело М сообщает тележке по­стоянное ускорение. При этом отвес отклоняется в сто­рону, противоположную ускорению на угол α. Величина отклонения угла α определяется однозначно ускорением тележки относительно инерциальной систе­мы отсчета и остается неизменной в последующем (?).

Рис. 33.

В этом рассуждении замаскирована ошибка. Она за­ключается в том, что тележка движется не относи­тельно инерциальной системы отсчета, а относитель­но Земли. И если относительно мыслимой системы отсчета, с которой тележка, естественно, не взаимодей­ствует, она кажется движущейся с постоянным нараста-нием скорости, не влияющей на ее физическое со­стояние (не меняющей ее качество). То при движении с постоянным ускорением по поверхности Земли измене­ние скорости движения сопровождается реальным из­менением взаимодействия тележ-ки с Землей, которое и вызывает соответствующее изменение угла отклоне­ния отвеса α, т.е. фиксируется новое качество тележ­ки.

Дата добавления: 2014-11-29